起重机吊重系统鲁棒滑模观测器设计
2014-03-27钟斌赵晓青
钟斌, 赵晓青
(中国人民武装警察部队工程大学 装备工程学院特种装备研究所,陕西 西安 710086)
桥式起重机或门式起重机(以下简称起重机)的吊重与小车之间采用钢丝绳柔性联接,在小车运行中控制吊重摇摆一直是控制学科学者研究的热点和难点[1-4]。对吊重摆角控制系统的设计往往需要小车位置与速度、吊重摆角与摆角角速度等状态变量信息[5-9],但由于吊重与小车之间柔性联接结构特点,往往不便于在现场安装传感器以测量吊重摆角与摆角角速度信息[10-11]。所以,文献[1] 利用神经网络能对任意函数逼近的原理,采用RBF神经网络,针对标准单输入、单输出的二阶系统,在基本状态观测器的基础上设计了神经网络状态观测器,将可测的起重机吊重摆角变量作为输入量,实现了对吊重摆角速度的观测,减少了对吊重摆角速度的现场测量成本,但是,这种方法仍须现场测量吊重摆角,测量成本仍然较高,并且无法观测出小车位移与小车速度,但往往小车位移和小车速度在吊重摆角控制系统中也是必需的反馈变量[11]。文献[2] 设计了Luenberger观测器,利用测量的小车位置信息对小车速度、吊重摆角及其角速度进行观测(估计),在该文献中,采用对观测器极点配置的方法研究了观测器对各变量观测速度与观测器极点在复平面中的位置之间的关系,理论研究和实际应用均表明所设计的Luenberger观测器对变化的吊重质量和起升绳长均具有一定的鲁棒性,并降低了测量成本。但实际应用中发现,当存在诸如外界较强风阻、实验台较强振动等外界影响时,对这些状态变量信息的状态观测结果与由系统建模得到的状态变量动态响应之间就会存在较大误差。实际上这些外界影响即是外界干扰,即系统建模中的未知不确定性项,如何设计对这些外界干扰也具有更强鲁棒性的状态观测器更具有广泛的工程实际意义。
为此,本文针对起重机吊重四阶系统设计了鲁棒滑模状态观测器,通过合理设计滑模面和滑模控制策略,使观测器对外界干扰引起的非线性不确定部分具有鲁棒性,从而渐近估计出系统状态变量,有效地改进了文献[1] 和[2] 所设计的观测器,实验表明本文所设计的鲁棒滑模观测器更具有工程实际意义。
1 起重机吊重不确定非线性系统及其可观性
起重机吊重系统几何描述如图1所示,小车质量为M,吊重质量为m,吊重摆角为θ,O点为小车参考位置原点,F为小车驱动力(N),l为起升绳长(m)。

图1 起重机吊重系统几何模型
由文献[1]的研究方法和步骤得到起重机吊重不确定非线性动力系统:
(1)

式中,D为轮轨摩擦阻尼系数。
f(t,X,u)=Bξ(t,X,u)
(2)
式中,ξ(t,X,u)是由于系统建模误差、噪声干扰等不确定状态造成的不确定函数,且ξ的上界已知,即:
(3)
式中,r1为已知正实数,α为已知函数。
(4)
(5)
由式(4)和式(5)可知Q1和Q2的秩均为4,所以(A,C)能观,即可以利用惟一变量x1(t)(即观测器的输入变量为x1(t))或同时利用x1(t)和x2(t)(即观测器的输入变量为x1(t)和x2(t))观测系统(1)的其余状态变量,获取所有状态变量信息。
2 鲁棒滑模观测器设计
对系统(1)设计鲁棒滑模状态观测器的目的是快速、准确地估计(观测)出系统的状态变量X(t),且设计的观测器对系统(1)中的非线性不确定性项f(t,X,u)具有鲁棒性。设计如下形式的鲁棒滑模观测器:
(6)

定义状态观测偏差(简称偏差)为:
(7)
则偏差系统微分方程为:
(8)
式中,A0=A-GC为观测器的动力学矩阵。
由式(8)可见,如果偏差系统的状态变量e(t)渐近地或在有限时间内收敛到原点,则实现了观测器的设计目的。为此,设计线性滑模函数:
s=Me(t)
(9)
式中,M∈R1×4,并令M=KC,且滑模参数矩阵K∈R1×2。于是:
(10)
由式(6)和式(10)可知,鲁棒滑模观测器系统结构如图2所示。所以,鲁棒滑模观测器的设计问题可归结为观测器增益矩阵G、滑模参数矩阵K和控制输入v的设计问题。
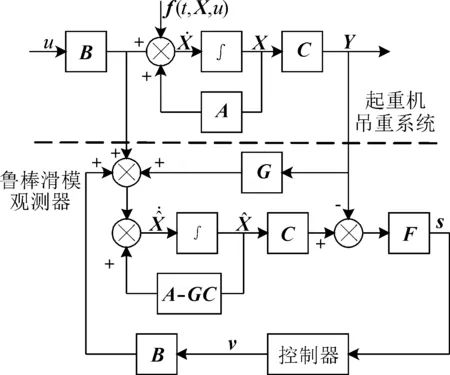
图2 鲁棒滑模观测器系统结构
设计滑模控制策略:
(11)
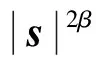
为了确定观测器增益矩阵G,考虑观测器的特征方程:
det[λI-A0]=0
(12)
式中,λ为观测器的特征值,对应观测器的4个极点λ1~λ4;I为4×4单位矩阵。
设观测器的极点分别配置在复平面的负实轴上,即-λi处(λi为实数,且λi>0,i=1,2,3,4);同时,为叙述方便,称λi为极点。则观测器的特征方程又可表示为:
(13)
由式(12)和式(13)中对应λ项的系数相等可知方程(14)成立。
HkGk=Rk(λi) (k=1,2;i=1,2,3,4)
(14)

其中:
r1=λ1+λ2+λ3+λ4
r2=λ1λ2+λ1λ3+λ1λ4+λ2λ3+λ2λ4+λ3λ4
r3=λ1λ2λ3+λ1λ2λ4+λ1λ3λ4+λ2λ3λ4
r4=λ1λ2λ3λ4
从而解得:
(15)
(16)
由式(15)可以看出,观测器增益参数g1~g4分别是极点λi的函数,由极点可以确定G1;由式(16)可以看出,通过合理选择g12(g12≠1)、g22、g32、g42和极点可以确定G2,从而保证A0为Hurwitz矩阵。
3 偏差系统稳定性分析

为了验证状态观测偏差系统的稳定性,证明定理1,选取Lyapunov函数:
(17)
沿偏差系统(8),V(s)对时间的一阶导数为:
eTMTM(A0e-Bξ+Bv)=
sTMBξ+sTMBv≤
(18)
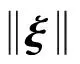
(19)
由式(19)知,偏差系统(8)到达滑模面s=0, 以后将渐近收敛到平衡点e=0。
4 数值仿真
起重机吊重系统参数:m=5 000 kg,M=2 000 kg,l=5 m,D=0.2,g=9.81 m/s2。
鲁棒滑模观测器设计参数:η=0.4,β=4,ρ=0.05,λ1=λ2=λ3=λ4=6。
若利用x1(t)变量,则:
K=[0.05]
G=[16.00 93.25 -8.65 0.01]T
若利用x1(t)和x2(t)变量,则:
系统和观测器的初值分别为:
小车驱动力u(t)=2000sint,不确定性未知函数ξ(t,X,u)=0.06sin(2πt)。


图3 状态变量及其观测信息

图4 状态变量观测偏差
从图3和图4可以看出,当选择小车位置信息作为观测器的输入时,各状态变量的观测值在约1.5 s时与其动态响应几乎完全重合,即各状态变量的观测偏差在约1.5 s时渐近地趋于零;当选择小车位置和速度信息作为观测器的输入时,各状态变量的观测值在约3.5 s时与其动态响应几乎完全重合,即各状态变量的观测偏差在约3.5 s时渐近地趋于零。
实验还表明,所设计的鲁棒滑模观测器对存在不确定因素导致的非线性不确定性部分具有鲁棒性(如图5所示),并且对不同形式的小车驱动力具有良好的适应性。

图5 存在不确定因素时状态变量的观测误差
5 结 论
起重机吊重系统鲁棒滑模状态观测器通过所测量的小车位置信息或小车位置与速度信息实现对系统状态变量的观测。
仿真实验表明:当选择小车位置信息作为观测器的输入时,各状态变量的观测偏差在约1.5 s时渐近地趋于零;当选择小车位置和速度信息作为观测器的输入时,各状态变量的观测偏差在约3.5 s时渐近地趋于零;观测器对系统中的非线性不确定项具有较强的鲁棒性,同时对不同形式的小车驱动力具有良好的适应性。
参考文献:
[1] 钟斌,赵晓青,胡雪艳.基于径向基函数神经网络观测器的设计及应用[J].西安理工大学学报,2013,29(3):352-356.
Zhong Bin,Zhao Xiaoqing,Hu Xueyan. Load’s swing angle velocity soft measure for crane based on neural network observer[J].Journal of Xi’an University of Technology, 2013, 29(3): 352-356.
[2] 钟斌.桥门式起重机吊重摆角软测量及仿真研究[J].系统仿真学报,2011,23(9):1985-1989.
Zhong Bin. Research on load’s swing angle soft measure and simulation for overhead or gantry crane[J].Journal of System Simulation, 2011, 23(9): 1985-1989.
[3] Wen J T, Popa D O, Montemayor G P L. Human assisted impedance control of overhead crane[C]//Proceedings of the 2001 IEEE International Conference on Control Applications. Mexico: IEEE Press,2008:383-384.
[4] 钟斌,蒋猛.基于小车位置的起重机吊重系统扩张状态观测器设计[J].西南大学学报:自然科学版,2014,36(8):173-177.
Zhong Bin, Jiang Meng. Design of extended state observer for the crane-load system based on trolley’s position information [J]. Journal of Southwest University (Natural Science Edition), 2014,36(8):173-177.
[5] Yong S K, Han S S, Seung K S. A new anti-sway control scheme for trolley crane system[C]//Proceedings of the 36th ISA annual meeting on industry applications. Piscataway: IEEE Press, 2006: 548-550.
[6] Kang G B, Kim Y B, An S B, et al. A new approach to anti-sway system design for a container crane[C]//Proceedings of SICE annual conference. Fukui: SICE Press, 2007:2289-2291.
[7] Liu J Y, Zhang I S, Nan X H. Based on the energy consumption of the smallest three-phase asynchronous motor optimize control of energy saving[C]//Proceedings of the Asia-Pacific Power and Energy engineering Conference. Chengdu: IEEE Press, 2010:1-4.
[8] 俞建蔚,肖健梅,王锡淮.基于滑模控制的集装箱起重机防摇控制[J].控制工程,2009,16(12):39-41.
Yu Jianwei,Xiao Jianmei,Wang Xihuai. Anti-swing system control of container crane based on sliding-mode method [J]. Control Engineering of China, 2009,16(12):39-41.
[9] 马莉丽,程文明,钟斌. 起重机电机拖动系统负载跟踪控制[J].西南交通大学学报,2013,48(3):494-499.
Ma Lili,Cheng Wenming,Zhong Bin. Research on load’s tracking control for crane’s motor driving system[J]. Journal of Southwest Jiaotong University, 2013,48(3):494-499.
[10] 杜鹏,赵雁,钟斌. 起重机吊重摆角子系统扩张状态观测器设计和仿真研究[J]. 机械科学与技术,2014,33(8):1203-1206.
Du Peng,Zhao Yan,Zhong Bin. The design and simulation of extended state observer for the crane load angle subsystem[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33 (8):1203-1206.
[11] 钟斌.基于吊重防摇控制的起重机快速对位关键技术研究[D].四川:西南交通大学,2007.
Zhong Bin. Critical technique for crane’s fast contraposition based on load’s anti-swing control[D]. Sichuan: Southwest Jiaotong University, 2007.
