陶瓷球轴承高精密电主轴临界转速分析*

刘高进，马会防，戴素江，陆勇星，李银海

（1.金华职业技术学院机电工程学院，浙江金华 321000；2.上海凯泉泵业(集团)有限公司，上海 201804）

高速数控机床是装备制造业的技术基础和发展方向之一，是装备制造业的战略性产业。其技术水平的高低和拥有量的多少也是衡量一个国家制造业水平高低的标志。作为制造技术产生第二次革命性飞跃的的一项高新技术，高速数控机床产生了巨大的经济效益。高速数控机床首先取决于电主轴，而电主轴关键技术包含高速精密轴承技术、动态性能技术、热态性能技术、高速电机技术等[1]。

国内外许多专家和学者对动态性能技术进行研究。目前常用方法就是先将轴承刚度用假设的弹簧替代，利用有限元技术计算主轴各阶固有频率和振型，并在设计时让转子系统的最高转速不高于一阶临界转速的0.75倍[2]。为了提高有限元仿真的准确度，彭必友等人将转子—轴承等零件作为一个系统进行动力学分析研究[3]；孟德浩等人分析了转子系统临界转速和转速与预紧力的关系[4]；李蓓智等人分析了主轴孔径和支撑刚度对模态参数影响[5]；李松生等研究了跨距、材料等对模态参数的影响[6]；Lin综合考虑了轴承热特性，轴承预紧力和刚度的影响，但只考虑了轴承的静态支撑刚度[7]。已有的研究在电机安装位置的变化对临界转速的影响缺少分析，本文主要针对该方面进行探讨。

1 轴承-主轴系统有限元模型建立

由于高速电主轴本身零件较多，每个零件的特性不同，且在实际加工过程中工况不同，目前没有一个有限元模型能够将电主轴实际加工的真实工况完全体现出来，因此需要将电主轴进行简化。

（1）在实际加工过程中，电主轴前端夹有刀具，且会有一定的轴向力和径向力，由于这些参数是非线性，且没有准确、有效的计算方法，因此为了便于分析，只考虑刀具的质量，并把它转化到轴承前端的长度上。

（2）根据转子系统基本理论，在实际分析过程中需要把转轴简化为同时具有质量、弹性和阻尼器件的模型。由于电主轴是一个连续弹性体且振型较简单，因此电主轴简化成无质量、无阻尼且只考虑径向刚度的模型。

在实际建模过程中，如图1所示的结构采用UG构建其三维模型，也为有限元分析的几何模型。

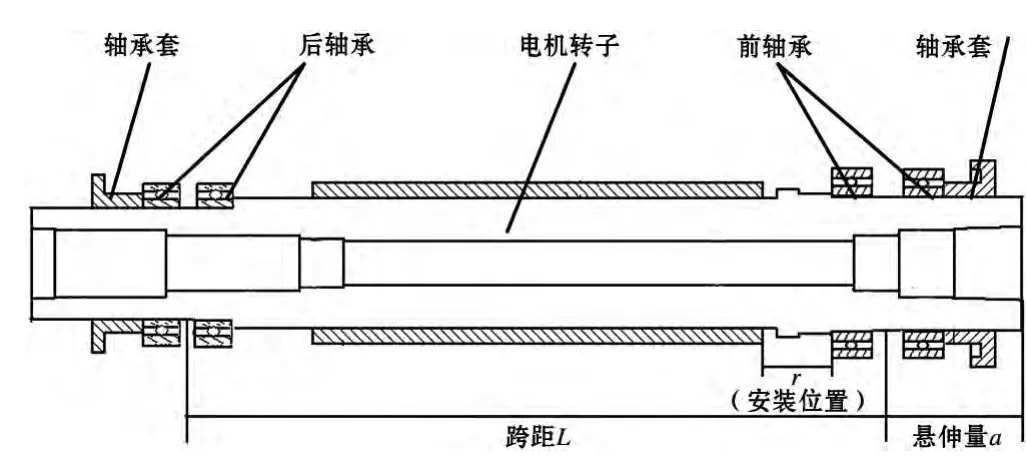
图1 电主轴结构图与模态参数

所设计的电主轴前后轴承均采用双联组配，且采用背靠背的组配方式，并在两轴承之间加隔离套。同时为了使电主轴具有足够的刚度，选择电主轴轴承配置方式为前轴承固定，后轴承浮动。前后轴承均为陶瓷球轴承，前轴承为7012C，后轴承为7010C。

2 转子系统刚度计算

2.1 预紧力的选择

电主轴的临界转速和许多因素相关，包括主轴的结构、支撑刚度、主轴的材料、跨距的大小、轴承的选择等等，其中支撑刚度对电主轴临界转速影响较大，而支撑刚度受预紧力的影响较大。

一般而言，预紧力越大，轴承的支撑刚度也越大，电主轴的临界转速越高；但另外一方面预紧力越大，轴向游隙越大，温升越高，可能造成烧伤，降低了寿命同时也降低了精度，这对高精密数控机床是不允许的，因此针对不同转速和负载的电主轴来选择轴承最佳的预紧力，成为电主轴制造厂家一个较为重要的技术。为了保证数控机床的精度，轴承内径与外径在50～80 mm之间的轴承，其轴向游隙必须在0～8μm。预紧力一般分为微预紧，轻预紧，中预紧，重预紧，对于不同厂家和不同型号的角接触轴承，对应预紧力的大小不同。根据厂家的规定，为了保证电主轴的精度，所选用的轴承均为微预紧。前轴承（7012C）预紧力为90 N，后轴承预紧力为75 N。

[11]中轴承的刚度模型，对于滚动轴承刚度由于各径向刚度基本相同，所以忽略其径向的耦合刚度，即Kxy=Kyx=0(N/m)，Kxx=Kyy=Kr，这样简化处理后的刚度模型如图2所示。

图2 轴向和径向支撑的刚度分析

2.2 系统径向刚度计算

轴承装配后的预载荷Gm用下面公式计算[8-9]

其中：

f为轴承系数，前端轴承内径为60 mm， f为1.88；后端轴承内径为50 mm， f为1.76；

f1为接触角系数，考虑所选轴承的接触角等因素，前后轴承 f1为1；

f2为预紧级别系数，前后轴承均为微预紧，f2均为1；

fHC为混合陶瓷球轴承修正系数，由于前后轴承均采用陶瓷球轴承，该值为1.06。

代入相应的公式，可分别计算出前后轴承的预载荷。

在确定了预载荷的情况下，可以计算出角接触轴承径向刚度Kr，公式如下[8]：

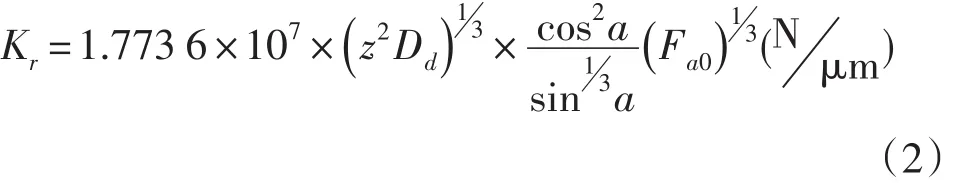
如果采用混合陶瓷球轴承，应该乘以修正系数1.3。

对于前轴承7012C，径向刚度：

后轴承7010C，径向刚度：

3 模态分析

多自由度模态分析的一般方程为：

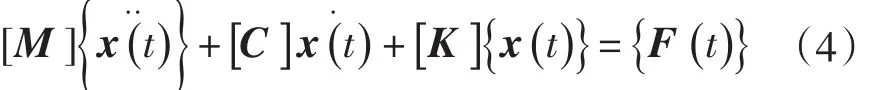
其中，[M]、[K]、[C]分别为总体质量、刚度、阻尼矩阵；{x (t)}、{F (t)}分别为节点的位移和外力向量。

当弹性体的动力基本方程中的外力向量{F (t)}={0}时，便可得系统的自由振动方程：

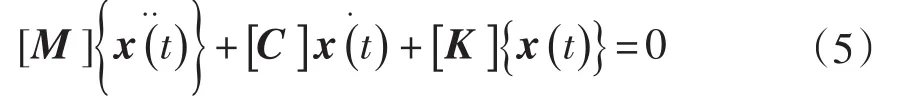
根据上式即可求解固有频率和振型[10]。

将所建转子模型导入ANSYS软件，其中主轴材料为20CrMnMoH，弹性模量为2.1×1011Pa，密度为7 850 kg/m3，泊松比为0.3，如图3所示。然后进行模态分析，得到以下固有频率，如表1所示。

图3 模态分析的模型图

其中，临界转速n(r min)计算公式如下：

f(H z)为固有频率。

从固有频率和振型可以看出，第1阶和第2阶结算结果属于同一阶振型，第4阶和第5阶也属于同一阶振型。因此，这6个结算结果实际上体现了四阶振型，其对应固有频率为1 338.5 Hz，2 255.9 Hz，2 883.6 Hz以及3 035.5 Hz。在电主轴转子系统中，为了安全，转子系统最高转速不会高于一阶临界转速的0.75，因为所设计的电主轴最高为25 000 r/min，远远低于一阶临界转速的0.75（60 097.5），因此是安全的。其中第一阶振型和第二阶振型如图4和图5所示。

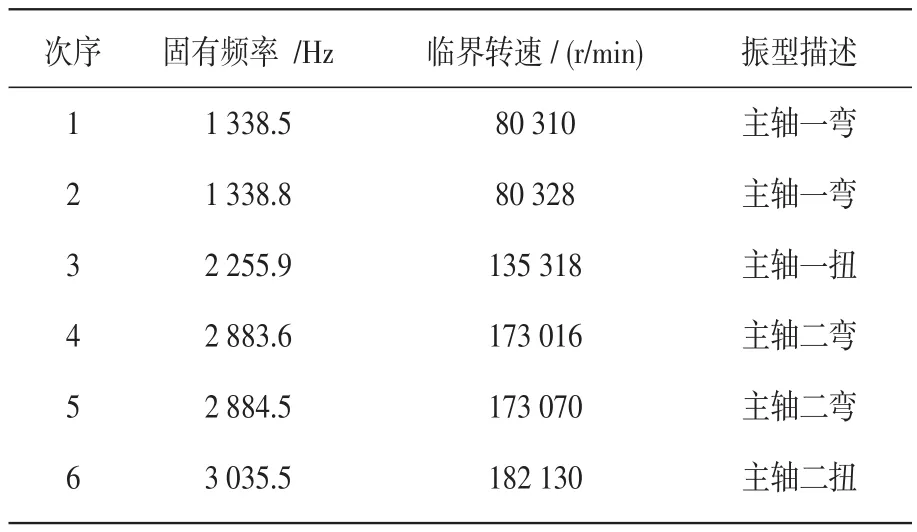
表1 电主轴各阶临界转速及振型

图4 一阶弯曲

图5 二阶扭曲

4 模态参数分析

在电主轴的工作过程中，转子系统的临界转速是一个很重要的参数，因为电主轴的最高转速必须小于临界转速的0.75倍，否则很容易发生共振导致转子系统损坏，因此必须提高转子系统的临界转速。

转子系统的临界转速和很多因素相关，比如说主轴结构、主轴材料、跨距大小、悬伸量长短、轴承载荷等。国内外许多学者对此做了大量研究，并得出许多结论。该文着重研究电主轴转子位置r对临界转速的影响，以及跨距L和悬伸量a对临界转速的影响，如图1所示。

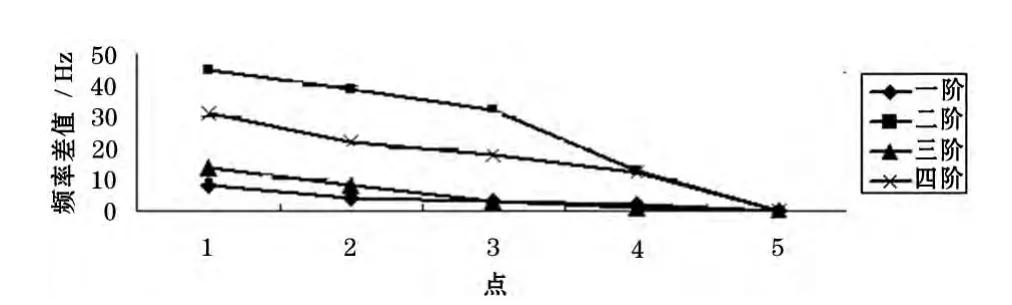
图6 电机转子安装位置与频率变化

通过分析，转子安装位置不同相对应临界转速也不同，频率变化量与安装位置变化量之间的关系如图6所示。素，比如说静刚度、电主轴结构等。目前往往将内装电机安装于两轴承之间，因为这样有利于提高整个轴系的寿命。

（3）改变悬伸量a、跨距L并计算出相应临界转速也不同，频率变化量与安装位置变化量之间的关系，如图7和图8所示。

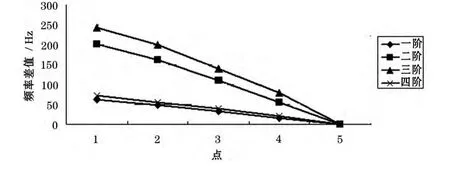
图7 电机悬伸量与频率变化

其中，横坐标为五个点，每一个点均相差10 cm，依次逐步往前轴承靠近，即1～5点对应r的值分别为10 cm，20 cm，30 cm，40 cm，50 cm。表一所计算的临界转速值即为r为30 cm处的临界转速值，从而可以计算出其他四点的临界转速值，同时从图6可以看出一些特性。

（1）电机转子安装越靠近前轴承，临界转速越高，但对整个转子系统临界转速影响不大。由于转子安装位置变化是有限的，比如所设计的电主轴支撑跨距为314 mm，而转子本身就有202 mm，再除去两个轴承及冷却的厚度，安装位置只能在0～60 mm之间浮动，从图6可以看出，当安装位置变化时，频率变化最大不会超过45 Hz，相对于临界频率（1 338.5 Hz）影响较小。

（2）安装位置变化对于一、三阶影响不大，但对二、四阶影响较大。从上面知道一、三阶是主轴发生弯曲，而二、四阶是主轴发生扭曲。因此，安装位置变化对弯曲影响较小，而对扭曲影响较大。

所以在电主轴设计过程中，往往不考虑安装位置变化对整体刚性的影响，而是看重其他因

图8 电机跨距与频率变化

图7 中，横坐标为五个点，依次远离前轴承。1～5点对应悬伸量a的值分别为在当前基础上依次延伸0 cm，10 cm，20 cm，30 cm，40 cm，表1所计算的临界转速值即为点1处的临界转速值，从而可以计算出其他四点的临界转速值。

图8中，横坐标为五个点，跨距依次增大。1～5点对应跨距L的值分别为在当前基础上依次增大0 cm，10 cm，20 cm，30 cm，40 cm，表1所计算的临界转速值即为点1处的临界转速值，从而可以计算出其他四点的临界转速值。

通过分析图6、图7、图8可以看出，临界转速影响因素排列顺序为：

跨距＞悬伸量＞安装位置。

而且，跨距变化对临界转速影响比较明显，而悬伸量和安装位置变化影响小很多。因此在考虑整个轴系的刚性时，要着重研究跨距L的影响因素。

5 结论

（1）分析轴承预紧力的选择。轴承预紧力越大，轴向游隙越大，运转时发热量越大，即精度和寿命都较低，但刚度越高，临界转速越高，反之亦然。因此对于高精密电主轴而言，轴承预紧力不能过大。

（2）对设计的电主轴进行模态分析，结果可以看出电主轴的最高转速小于一阶临界转速的0.75倍，符合要求。

（3）对影响临界转速的模态参数分析。分析结果可以看出安装位置变化对临界转速影响较小，因此对于电主轴厂家在考虑电机转子安装位置时主要分析其他因素，比如说静刚度，整体结构等。

（4）对比模态参数对临界转速的影响程度可以看出，跨距影响最大，悬伸量次之，最后是电机安装位置。

影响临界转速的模态参数还有很多，可以对比这些模态参数的影响程度，为电主轴的设计提供宝贵的建议。

参考文献：

［1］吴玉厚.数控机床电主轴单元技术［M］.北京：机械工业出版社，2006.

［2］马会防.滚动轴承径向刚度在转子临界转速计算中的应用［J］.轴承，2013（4）：33-35.

［3］彭必友，胡腾，傅建，等.加工中心电主轴复合“转子—轴承”系统动态特性研究［J］.西华大学学报：自然科学版，2013（1）：82-87.

［4］孟德浩，龙新华，孟光.高速电主轴转子——轴承系统动态特性分析［J］.噪声与振动控制，2012（4）：7-12.

［5］李蓓智，吴喜如，杨建国，等.精密数控车床电主轴-轴承-转子系统动态性能计算分析［J］.机械设计与制造，2010（3）：173-175.

［6］李松生，张刚，陈晓阳，等.高速电主轴球轴承——转子系统动力性能分析［J］.机械科学与技术，2006（12）：1447-1470.

［7］ Lin， C.-W. ， J.F.Tu， et al.An integrated ther⁃mo-mechanical-dynamic model to characterize motor⁃ized machine tool spindles during very high speed.rota⁃tion ［J］.International Journal of Machine Tools and Manufacure，2003，43（10）：1035-1050.

［8］戴曙.机床滚动轴承应用手册［M］.北京：机械工业出版社，1993.

［9］NSK LTD.NSK滚动轴承技术手册［Z］.2009.

［10］傅志方，华宏星.模态分析理论与应用［M］.上海：上海交通大学出版社，2000.

［11］钟一諤，何衍宗，王正，等.转子动力学［M］.北京：清华大学出版社，1987.