一种新的并联机器人精度标定算法

余杰先，吴 朋，曾 奇

（广东工业大学机电工程学院，广东广州 510006）

0 引言

工业机器人近年来发展迅速，而机器人的绝对精度[1]成为了限制机器人行业发展的瓶颈之一。在Delta高速并联机器人的精度标定课题中，机器人末端位置误差的测量决定了标定实验是否能够实现。末端位置误差的测量方法有黄田教授等采用的间接测量法[2-4]，这种方法以第一测量点为理想点，测量的结果带入了机器人结构参数误差，或者以标准件为理想坐标点，然而机器人末端触及到标准件存在着较大的误差，并且没有实现测量坐标系与机器人坐标系的转换。Pierre Renaud等人利用视觉的误差测量法[5-7]，这种测量方法本身在视觉系统标定时，虽然实现了摄像机坐标系与Delta机器人坐标系之间的转换，然而，摄像头本身标定时就存在着误差，而且当机器人末端触碰标定点时也存在着较大误差。本文以PA控制器为实验对象，不再借用激光跟踪仪，从而忽略了靶球夹具带来的制造和装配误差，只需要测量机器人动平台的z向偏差即可，然后借助本文中提出的算法，进行误差识别。从而进行对控制器中的运动学参数补偿。

1 误差辨识原理

1.1 误差模型

根据实际应用，由于Delta并联机器人的三条臂具有对称性，所以，可以得到简化后的误差模型如图1所示。

根据图1所示，得到Delta并联机器人关节链参数如下：

静平台的坐标系O-xyz：xy平面是三个电机的理想转动副所在的平面，其中x轴通过第一条主动臂。

静平台的坐标系Oi-xyz：以分布角为(i × 120°)的过渡坐标系，绕O-xyz的z轴转动分布，其中i=1、2、3。

动平台过渡坐标系：O‘-xyz，与O-xyz同姿态。

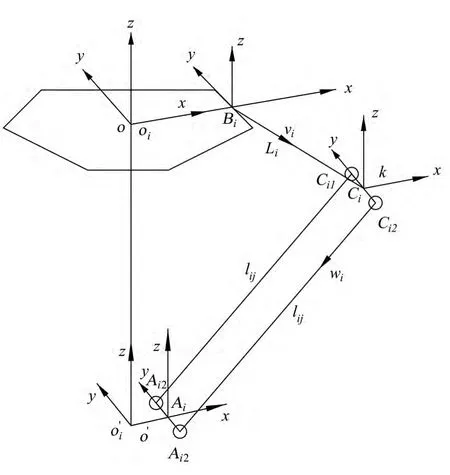
图1 并联机器人单链误差模型

主动臂参考坐标系：Bi-xyz，与Oi-xyz同姿态，只是沿x方向平移了Ra的距离，Ra是静平台三个电机输出轴回转幅所在分布圆的半径。

主动臂球铰坐标系：Ci-xyz，与Bi-xyz同姿态，只是沿着主动臂方向平移了Livi。

从动臂球铰坐标系：Ai-xyz，与-xyz同姿态，只是沿着主动臂方向平移了Livi。

根据误差模型可以得到该Delta机器人的全误差项如表1所示。

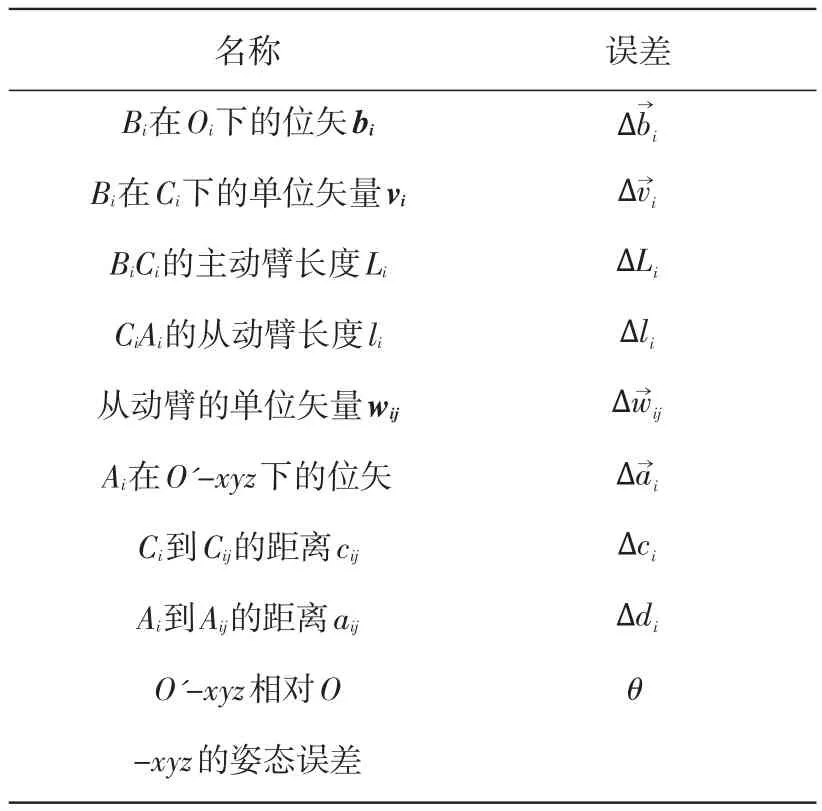
表1 Delta误差项

然而，根据实际使用中的机器人建模方法，一般配置的Delta机器人参数为：主动臂分布圆的半径Ra、主动臂分布角(i × 120°)、主动臂的长度Li、从动臂的长度li、动平台的球铰分布圆半径ra。

并且Delta机器人基座的基础精度包括了主动臂分布圆的半径以及分布角，而这两项的标定已经可以轻松地完成[5]。因此，需要标定的运动学参数一般就只剩下了主动臂的长度误差∆Li，以及从动臂的长度误差∆li。

1.2 误差辨识算法的推导

根据图1简历的误差模型，利用空间链的方法，可以将动平台中心位置相对于Delta机器人基坐标系的矢量 p→表示为：

对（1）和（2）式，按照泰勒级数展开，并忽略其高次相得到：

其中：i=1、2、3；

R→i是坐标系Oi-xyz相对于坐标系O-xyz的姿态矩阵；

θA是Ai-xyz相对于坐标系O'i-xyz的姿态误差矩阵。

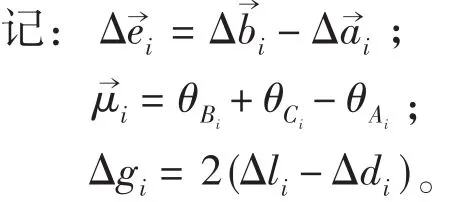
将方程3的左右两边同时乘以－→wi，然后将属于i条支链的闭环方程相减，然后再将属于第i条支链的闭环方程相加，将相减得到的方程，带入相加得到的方程，可以得到Delta机器人的关节误差辨识方程：

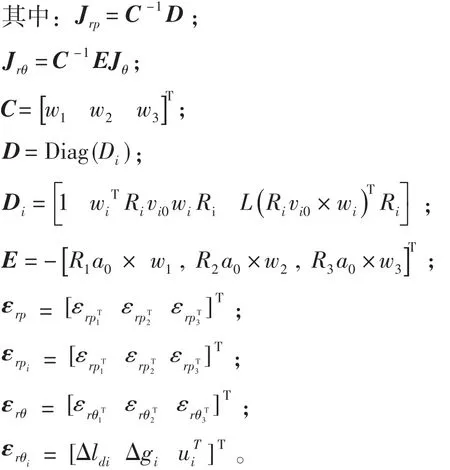
1.3 误差辨识模型的简化

在实际应用时，控制模型的建立比较简单，只需要输入Delta的主动臂分布角及其分布半径，主动臂长度，从动臂长度，动平台分布圆半径。由于现实的建模限制，可以将模型简化。

将表1中的三条主动臂的长度认为是具有同样的长度与误差，三条从动臂的长度认为是具有同样的长度与误差，而主动臂分布角误差导致的项已经可以较方便地标定出来[8]，其他的误差项可以通过基础零件的检测控制其误差，故都可以认为是0。基于此，（4）式可以简化为：

如此，如果可以测量得到Δp→中，任何一行的误差，数据采样的个数大于3的话，就可以方便地构造出Δp→的伪逆，从而求出εrp，即：

1.4 末端位置误差测量方法

让Delta机器人在事先加工好的标准平面上以同一个z向坐标随机地走动，同时在机器人末端加上一个千分表，以第一点的千分表的读数作为参考值，随机地暂停机器人记录其内部坐标读数与对应的千分表读数。用作误差辨识用。

2 仿真数据

为验证该标定方法的有效性，假定机器人存在关节误差，设定为ΔLi=2 mm、ΔIi=4 mm。

利用更改了运动学参数之后的模型的正解，求得Delta机器人实际所到达的位置，而利用理想的运动学参数模型正逆解来求机器人理想应该到达的位置，而两者之间的位置差就作为末端误差。

如此，得到表2和表3所示数据。

表2 理想的末端位置

表3 实际的末端位置与z向误差

利用上述两个表中的数据，带入到（7）式中，可以求出的辨识误差是：

ΔLi=1.476 8 mm，Δli=3.390 3 mm。

将ΔLi与Δli放到运动模型中进行参数补偿后的位置如表4所示。标定前后的精度对比提高了7.45倍。

表4 参数补偿后的位置

4 结论

本文结合实际工程应用，对Delta并联机器人的误差标定模型进行简化，适应了实际的使用需求，调高了并联机器人的绝对精度，证明了该方法的有效性。然而，本文仍然存在不足，比如末端误差的测量方法上，本文中采用的方法虽然简单、高效、成本低，然而以第一点作为参考误差值，还是不能绝对准确地反应机器人的绝对误差，因此会影响到标定的效果，接下来要做的工作是对末端位置的误差测量做进一步的研究。

［1］ MarkW.Spong，M.Vidyasagar.Robot Dynamics and Con⁃trol［M］.2nd，New York，USA： Wiley，2004.

［2］唐国宝，黄田.Delta并联机构标定方法研究［J］.机械工程学报，2003，39（8）：55-60.

［3］ Deblaise D，Maurine P.Effective Geometrical Calibra⁃tion of Delta Parallel Robot Used in Neurosurgery［A］.2005 IEEE/RSJ International Conference on Intelligent Robots and System ［C］.Piscataway， NJ， USA：IEEE，2005：1313-1318.

［4］ Zhu Yanhe，Yan Jihong，Zhao Jie，et al.Autonomous Kinematic Self-Calibration of a Novel Haptic Device［A］ .2006 IEEE/RSJ International Conference on Intel⁃ligent Robots and System ［C］.Piscataway， NJ，USA：IEEE，2006：4654-4659.

［5］ Renaud P，Andreff N，Marquet F，et al.Vision-based⁃kinematic calibration of a H4 parallel mechanism ［A］.2003InternationalConference on Robotics and Automation［C］.Piscataway， NJ， USA： IEEE， 2003：1191-1196.

［6］ Renaud P，Andreff N，Lavest J M，et al.Simplifying the Kinematic Calibration of Parallel Mechanisms Using Vision-Based Metrology ［J］.IEEE Transaction on Ro⁃botics，2006，22（1）：12-22.

［7］TraslosherosA，Sebatian J M，Castilo E，et al.One Cam⁃era in Hand for KinematicCalibration of a Parallel Robot［A］.2010 IEEE/RSJ International Conference on Intel⁃ligent Robots and System ［C］.Piscataway， NJ，USA：IEEE，2010：5673-5678.

［8］ 曾奇，刘冠峰.并联机器人基座标系精确定位集合算法［J］.机电工程技术，2013（10）：21-24.