同步电机自传感参数辨识技术

邓先明，王 磊，郭其锋

(中国矿业大学 信息与电气工程学院，江苏 徐州 221116)

由于同步电机具有功率因数可调节、效率高、容量大等优点，它在电力驱动领域使用得越来越多。为了保证电力驱动系统的可靠运行，对电机的温度和参数监测显得格外重要。目前，温度检测主要采用埋设在电机内部的温度传感器来测量电机温度。这些检测方法需要外部机械传感器，传感器存在安装困难、维护量大、可靠性不高等问题。针对上述问题，本文提出一种利用电机的自传感理论来测量电动机温度的方法。自传感方法是利用电压和电流传感器测量绕组的电压量和电流量，再结合电机本身的电磁特性，计算出相应的电机参数和状态信息，不需要外加机械传感器。

在同步电机驱动控制系统中，需要利用电机的阻抗参数来设计调节器参数。但是电机绕组电阻会随着温度变化，如果调节器参数不跟随绕组电阻变化就会影响控制系统性能。为了对同步电机进行精确控制，需要在线辨识电机参数，动态修改控制模型。

目前电机的参数在线辨识方法主要包括卡尔曼滤波器法[1]、最小二乘法[2]、状态观测器法[3]、模型参考自适应法[4-5]、高频信号注入法[6-7]和神经网络[8-9]等高级智能算法。最小二乘法能较好地对电机参数进行辨识，但计算量较大，需要高速控制器。状态观测器法将电机辨识参数作为状态变量，利用确定系统来对该参数进行估计，计算量较大。卡尔曼滤波器法计算量大。高频信号注入法在电机运行时注入高频信号，通过检测高频信号响应，对参数进行辨识。对于人工神经网络等智能算法，硬件实现困难，应用也不太理想。本文提出一种基于自传感理论的参数辨识方法，不需要外加的任何机械装置，利用电压电流传感器所得到的转子电压电流信号，就可以对电机定子电阻进行较为准确的辨识，且原理简单，实现非常容易，能够满足控制系统对定子电阻变化实时性的要求。

1 同步电机的损耗和发热分析

1.1 同步电机的损耗和发热分析

同步电机的损耗功率包括定子铜耗pcus、转子铜耗pcur和空载损耗p0。当电机的负载发生变化时，定子和转子铜耗都会变化，同步电机的损耗能量会全部转化为热量，一部分的热量被电机吸收使其温度升高，另一部分热量通过内部通风孔和电机表面散发[10-11]。由能量守恒原理可知，电机的发热量与吸热量、散热量应该平衡，即满足如下方程：

(1)

式中，Q是单位时间发热量；C是热容量；A是散热系数；τ是温升;t为时间。

由式(1)可知，当电机连续工作一段时间后，电机的温升将达到稳定值。但是，电机内部不同部位的发热量和散热系数等存在一定差异，因此电机内部各部分的温度不同。为了分析同步电机内部的温度情况，下面用有限元法对同步电机的温度进行分析。

1.2 有限元仿真分析

一段时间后，电机绕组电阻值和机壳温度基本稳定。电机负载运行时，定子绕组和转子绕组均为发热源，因此定子和转子绕组的温度不仅仅与绕组本身的温升、环境温度有关，发热源之间也通过传热相互影响。因此，同步电机定子绕组和转子绕组的温度关系为：

(2)

式(2)中，θs为定子绕组温度；θr为转子绕组温度；ks为定子传热系数；kr为转子传热系数；θ0为环境温度；θ1为冷却空气温度；Qs为定子总发热量；As为定子散热系数；Qr为转子总发热量；Ar为转子散热系数。

根据式(2)，首先确定发热源之间的相互传热系数ks和kr，本文分析电机的ks为0.212 7，kr为0.023 24。转子绕组给定子的传热系数ks比定子绕组给转子的传热系数kr大很多[12]。然后再根据式(2)计算定子绕组单独发热的温升τs和转子绕组单独发热的温升τr关系。

本文采用有限元软件Ansys对样机进行有限元仿真分析。仿真计算得到的不同负载下的定子和转子绕组温升如表1所示。

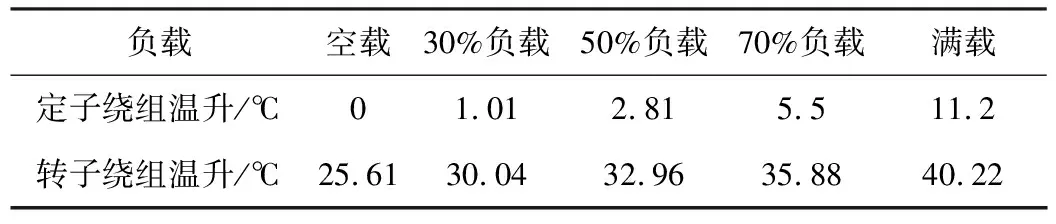
表1 不同负载下定子和转子绕组温升

利用式(2)，结合表1可以计算出基于转子绕组温度的定子绕组温度估算值，以及基于定子绕组温度的转子绕组温度估算值，如表2所示。环境温度为30 ℃，转子内冷却空气温度为40 ℃。

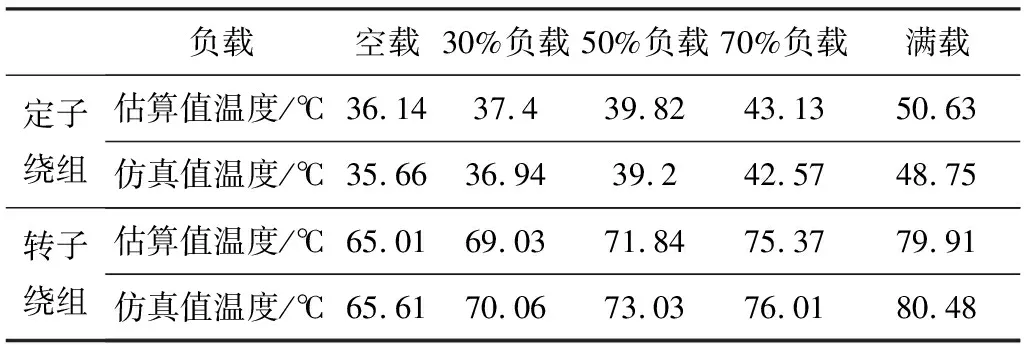
表2 不同负载下电机绕组温度的估算值和仿真实验值

由表2可以看出，绕组温度估算值与实际值基本吻合，误差很小。

2 基于自传感的同步电机温度监测

2.1 基于自传感的同步电机温度监测原理

基于自传感的同步电机的参数辨识电路原理如图1所示。在电励磁同步电机运行时，转子绕组经过电刷与外加直流励磁电源联通。转子励磁回路的电阻由励磁绕组电阻Rr和电刷接触电阻Rb构成。转子侧的电压Ur和电流量Ir可通过电压传感器和电流传感器直接测量得到，因此转子绕组电阻值为

Rr=Ur/Ir-Vb

(3)

图1 基于自传感的同步电机参数辨识电路

由于电机的转子绕组一般由铜材料制成，因而绕组的电阻值与温度呈线性关系，其关系式为

Rr=R0×(1+α×θ)

(4)

式中：Rr是θ℃时的绕组电阻；R0为是0 ℃时的绕组电阻；α是绕组电阻温度系数。

一般铜绕组电阻温度系数α=(3.93～4.0)×10-3℃-1。Rr值通过式(3)直接测得；R0值可以通过测量冷态时的电阻值和温度值直接算出；因而温度θ可以由式(4)很方便地求出。

2.2 实验验证

先用直流方法测出同步电机转子绕组的冷态电阻值和电刷接触电阻值。然后给转子绕组加直流电压，使电流达到额定值，电机温度会逐渐升高。在电机升温的过程中每隔1 min记录转子绕组的电压值、电流值和温度值，直至电机温度稳定。待电机温度稳定后，断电，使电机自然冷却，每隔1 min记录此时的定子和转子电阻值和温度，直至冷却至室温。所采用的同步电机参数：额定输入功率200 W，额定电压220 V，定子额定电流0.6 A，额定励磁电流1.2 A。

实验测得的冷态时转子电阻值为9.7 Ω，温度为14 ℃。实验数据经处理后所得的升温时的转子电阻随温度变化曲线见图2,测得值与计算值比较见图3。

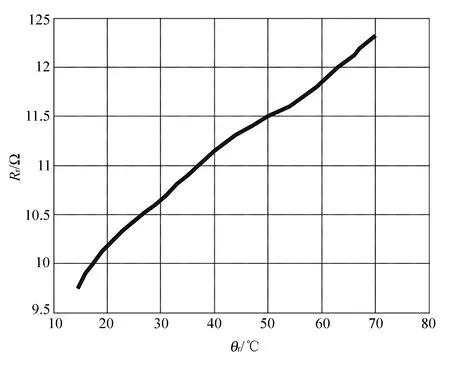
图2 转子电阻随温度变化曲线

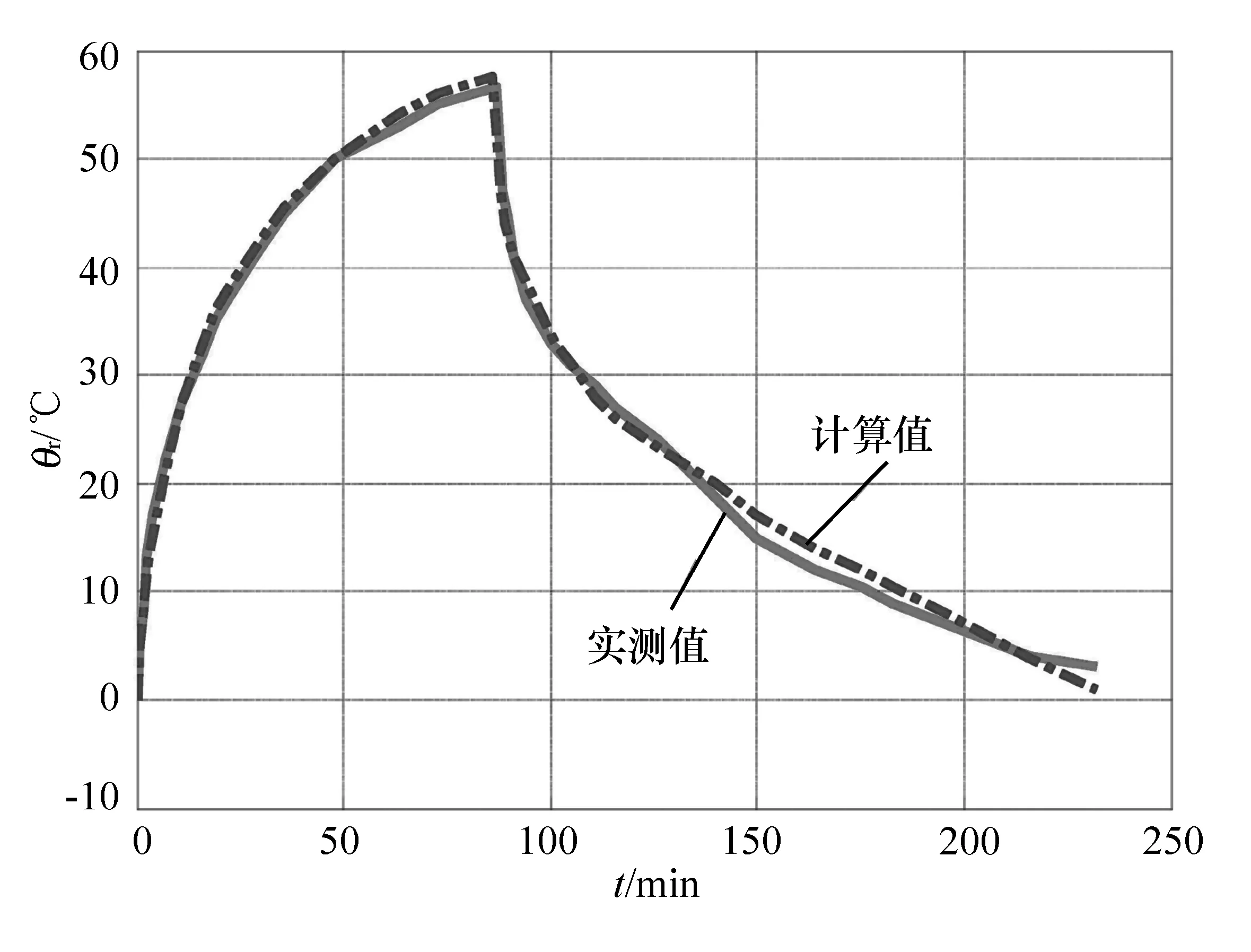
图3 转子温度实测值和计算值比较

从图2中可以看出，在电机升温过程中转子电阻与温度基本呈线性变化关系。由图3可以看出，估算温度值与实测温度值基本吻合，因而通过本文提出的温度自传感检测方法可以很好地对温度进行检测。

3 基于自传感的同步电机定子电阻辨识

3.1 基于自传感的同步电机定子电阻辨识原理

3.1.1 基于转子绕组温度的定子绕组温度辨识方法

由上述电机温度场有限元分析可知，由于定子绕组和转子绕组本身的发热量不同，定子绕组和转子绕组本身的温升会有差异。但是，可以利用转子绕组的温度结合式(2)来估算定子绕组温度。

先离线测出电机定子的传热系数ks和散热系数As。然后在线测出定子和转子损耗功率和转子绕组温度，最后利用式(2)计算出定子绕组温度。

3.1.2 定子绕组电阻辨识的原理及方法

同步电机的定子绕组一般也采用铜材料制成，定子电阻值也与温度呈线性关系。因而只需要知道电机定子的温度就可以通过式(4)实现对定子电阻的准确估算。在认为转子电阻温度与定子电阻温度相同时，有

(5)

式(5)中，R0s、R0r分别为0 ℃时的定子电阻和转子电阻，R0s和R0r都可以由冷态时的电阻值通过式(4)直接计算得到。

考虑定子和转子电阻发热差异导致的温度差异，通过式(5)来计算定子电阻必然带来较大的误差，本文采用式(2)计算得到的定子温度,再通过式(4)对定子电阻进行计算，而得到较为准确的结果。

3.2 实验验证

将同步电机定子绕组首尾串联，施加直流电压并使电流达额定值，同时在转子绕组中也加额定的直流电流，使电机升温直至电机温度稳定。在电机升温的过程中每隔1 min记录定子绕组电压和电流、转子绕组电压和电流值。

测得冷态时定子A相电阻为16 Ω、B相电阻为16 Ω、C相电阻为15.9 Ω。

利用测得的定子绕组电压和电流，根据欧姆定律计算出定子绕组的实际电阻值。利用转子电阻结合公式(2)和(4)可以计算出定子绕组电阻值。

图4—图6为定子(A、B、C三相绕组)电阻(分别记RA、RB和RC)与温度变化曲线，其中虚线是定子电阻计算值曲线，实线是定子电阻实测值曲线。可以看出，通过转子温度先估算定子各相绕组温度值，然后再计算定子各相电阻值与实际值相比误差很小，基本能实现对定子电阻变化的准确跟踪。因而通过本方法可以对定子电阻进行较为准确的估算，能够满足控制系统的要求。

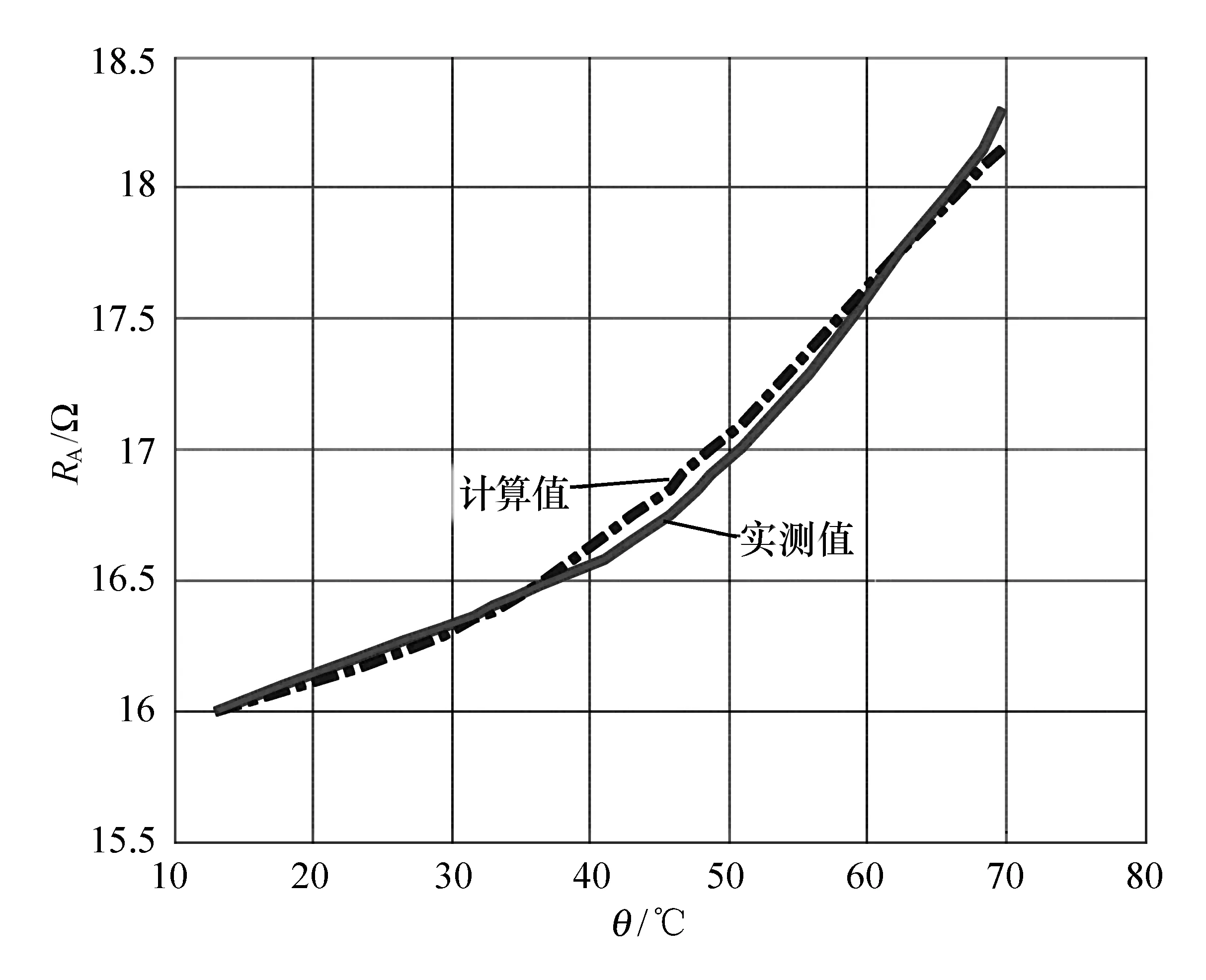
图4 A相电阻曲线

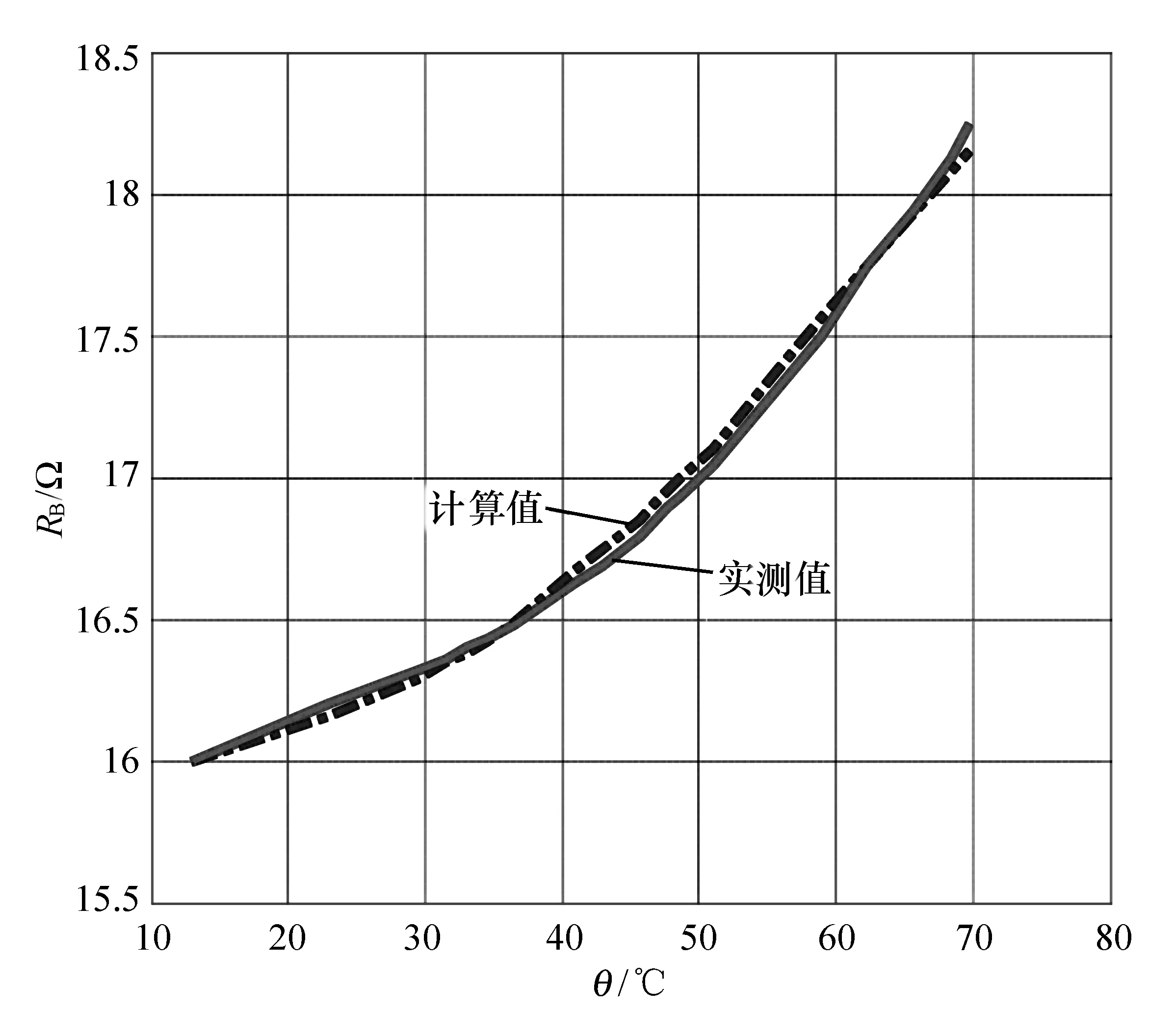
图5 B相电阻曲线

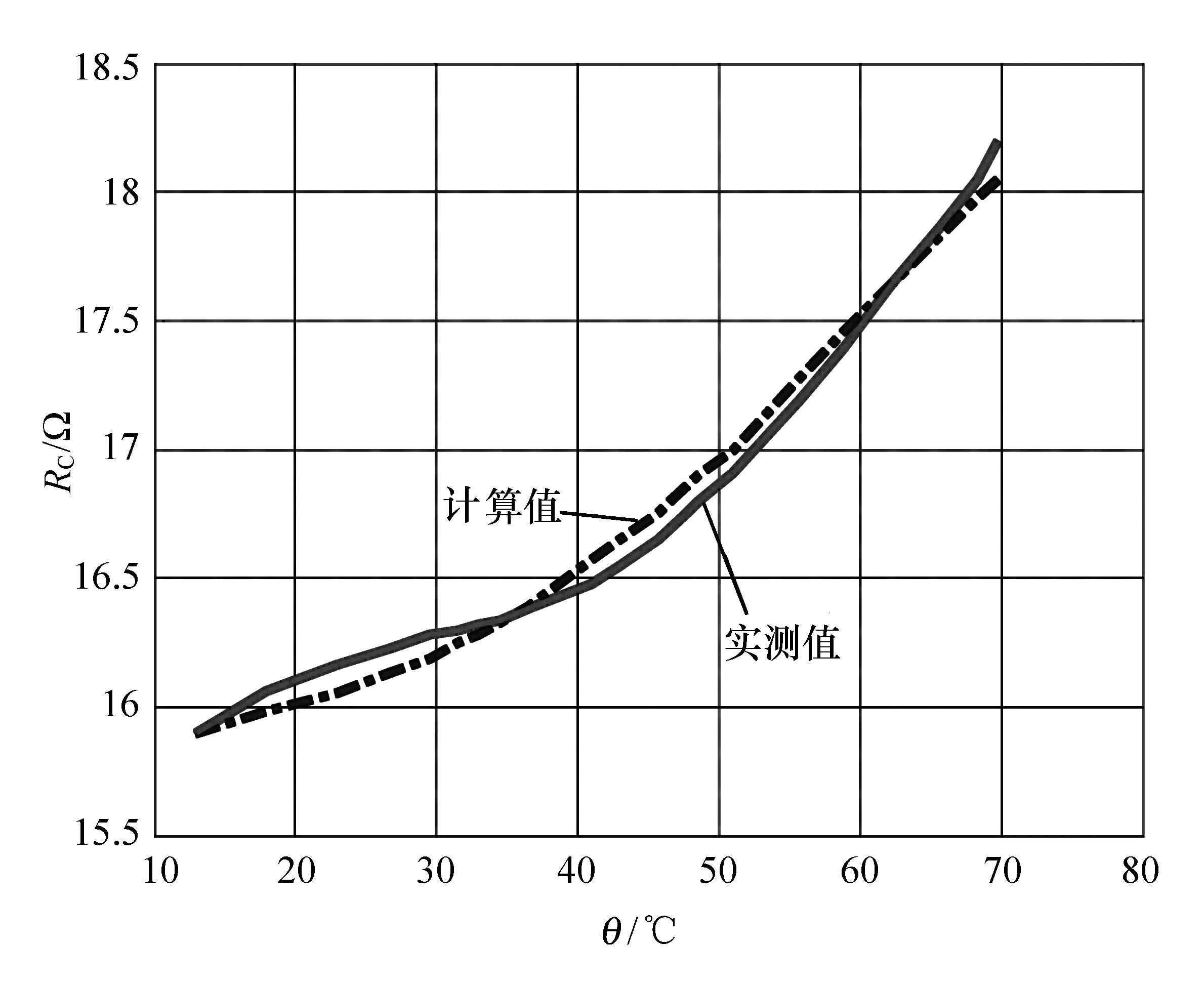
图6 C相电阻曲线

4 结论

本文提出了一种对转子电阻温度、电阻和定子电阻值的在线辨识技术。本方法不需要其他额外的机械传感器，通过基本的电压和电流传感器所得的绕组电压和电流值，再利用绕组材料的温度特性，就可以对绕组温度和电阻进行准确的在线辨识。 通过同步电机的堵转升温实验，对本方法进行了验证。结果表明，本文提出的方法能对定子和转子温度和定子电阻进行较为准确的在线辨识，能够满足控制系统的要求，具有较好的辨识精度和实用性。

[1] 赵歆，王明渝，刘述喜.基于扩展卡尔曼滤波器的异步电机矢量控制系统的转子电阻辨识[J].电机控制与应用，2009，36(3)：18-23.

[2] 吴旭升，张俊洪，刘颖奇.带交轴短路绕组的同步电参数局部辨识[J].电机与控制学报，2009，13(增刊1)：1-5.

[3] 张细政，王耀南，杨民生.电动车用感应电机电阻的状态滑膜观测新方法[J].中国电机工程学报，2009，29(15)：101-106.

[4] 王瑞，赵金，丛喆，等.基于MRAS的转子时间常数辨识方法的参数敏感性分析[J].电气传动，2010，40(1)：3-7.

[5] 刘述喜，王明渝，陈新岗，等.基于数字信号处理器的异步电机参数辨识实现[J].电机与控制应用，2006，33(10)：21-30.

[6] 万山明，吴芳，黄声华.基于高频电压信号注入的永磁同步电机转子初始位置估计[J] .中国电机工程学报，2008，33(28)：82-86.

[7] Ciro Attaianese, Giuseppe Tomasso.Position Measurement in Industrial Drives by Means of Low-Cost Resolver-to-Digital Converter[J] .IEEE Transactions on Instrumentation and Measurement, December ,2007,56(6):2155-2159.

[8] 刘侃，章兢.基于自适应线性元件神经网络的表面式永磁同步电机参数在线辨识[J].中国电机工程学报，2010，30(30)：68-73.

[9] Salvatore, Cupertino L, Cascella F, et al.A new approach to sensorless vector control of SPMSM with adaptive sliding-mode observer[J].Proceedings of the 2002 IEEE International Symposium，2002，2(4):489-494.

[10] 吴海鹰.大中型永磁电机温度场数值计算[D].武汉：华中科技大 学，2007.

[11] 靳廷船.多功率异步电动机电磁场和温度场的数值计算与分析[D].哈尔滨:哈尔滨理工大学，2006.

[12] 温志伟.基于数值分析的大型同步电机内温度场的研究[D].北京：中国科学院研究生院，2006.