残差修正的GM(1，1)模型预测路基沉降量

2014-03-25郭亚宇

陕西理工大学学报(自然科学版) 2014年6期

郭亚宇

(1.陕西铁路工程职业技术学院轨道工程系，陕西渭南 714000；2.兰州交通大学土木工程学院，甘肃兰州 730070)

0 引言

路基的工后沉降预测在高速铁路、客运专线建设中具有重要意义，但由于各种理论计算方法本身的局限性及地质条件的复杂性，完全依靠理论计算有时是不精确或不可能的。因此，常常需要根据前期实测沉降资料来预测后期沉降。目前利用沉降观测资料，分析预测工后沉降的方法很多，常用的有双曲线法、指数曲线法、三点法(对数曲线法)、星野法、沉降速率法、增长曲线法等等。但路基沉降是一个复杂的过程，它的影响因素较多，如地基的环境条件、地基土的应力历史、路堤填土的工程性质、路堤填筑的高度和施工工期等，这些因素都不同程度地影响和制约着路基沉降。用上述单一方法推求工后沉降存在较大的误差，所以可以考虑运用灰色系统理论，把路基沉降看成一个灰色系统，建立灰色预估模型以分析路基沉降的发展变化。其中在沉降预测中应用最为广泛的是灰色理论中的GM(1，1)模型。然而预测实践表明，以普通GM(1，1)进行预测，用于中长期时，若灰参数a小于零，则x(1)(t)趋近于a/b，实际上a/b即为路基的最终沉降量，此时效果甚佳[1]。但若灰参数a大于零，则x(1)(t)趋近于零，显然不符合实际情况，这时就会出现较大偏差，甚至完全失效。对此，本文提出了改进措施，引入残差修正的GM(1，1)预测模型，用于高速铁路某试验段路基的沉降预测。实例验证表明，残差修正模型的预测精度明显高于普通GM(1，1)模型。

1 普通的GM(1，1)模型

取相同时间间隔内的沉降增量数据序列X(0)为原始沉降数据序列，

X(0)={x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)},

(1)

其中x(0)(i)≥0,i=1,2,…,n。

对式(1)所示原始沉降数据序列作一次累加生成，可以得到一次累加生成序列X(1)，

X(1)={x(1)(1),x(1)(2),x(1)(3),…,x(1)(n)},

(2)

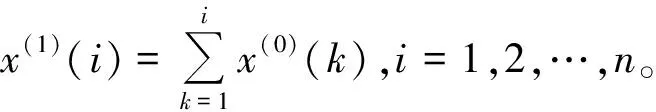
记z(1)为X(1)的紧邻均值生成序列，

Z(1)={z(1)(1),z(1)(2),…,z(1)(n)} ，

(3)

其中，z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1),k=1,2,…,n。

根据灰色理论GM(1，1)模型，可以建立灰色微分方程[2]，

x(0)(k)+az(1)(k)=b,

(4)

其中a，b是需要通过建模求解的参数，可按最小二乘法求解：

(5)

则白化形式微分方程的解或称时间响应函数为

(6)

GM(1，1)模型灰色微分方程x(0)(k)+az(1)(k)=b的时间响应序列为

(7)

取x(1)(0)=x(0)(1)，则还原序列为

(8)

2 残差修正的GM(1，1)模型

2.1 理论依据

当GM(1，1)模型对沉降序列进行预测时，如果模型检验精度不通过，或检验精度属于勉强通过，则可通过建立残差修正的GM(1，1)模型来提高精度。该方法是针对已建立的GM(1，1)模型得到的残差数列进行残差修正建立的。这个方法的实质是在已经得到的GM(1，1)模型的某项(就是残差开始变大的时间点处)加上一个修正项，其它时间点处的值不变，从而达到部分修正模型、提高精度的目的。

2.2 模型的建立

如2.1所述，当按照原始沉降序列X(0)建立的模型经检验不合格，或者虽然通过模型检验，但预测精度不高，这时可以考虑建立残差模型对原模型进行修正[3-5]。

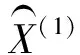
(9)

其中a′，b′为残差模型的参数值；当k≥i时，δ(k-i)=1，否则δ(k-i)=0。

2.3 模型的求解

模型的求解计算过程比较繁琐，本文引入MATLAB软件编程求解，使计算大大简化。MATLAB基本的数据单位是矩阵，它可以直接进行矩阵的乘积、乘方、除法、逆运算等。在MATLAB语言系统中，几乎所有的操作都是以矩阵操作为基础。而在残差修正的GM(1，1)模型灰色预测过程中，要进行大量的数列和矩阵运算，这使得MATLAB恰好派上了用场。本文在MATLAB程序编制过程中，结合灰色GM(1，1)模型和残差修正的GM(1，1)模型，编制了相应的M文件，在路基沉降预测过程中可直接调用相应的M文件，实现了计算的自动化，降低了劳动强度，使得预测效率大幅提升。

3 预测模型精度的评价方法

建立了沉降预测的GM(1，1)模型和残差修正的GM(1，1)模型后，为了比较和评定沉降预测模型的可信度，必须对模型的精度进行评定[6]。常用的评定方法有以下两种：

(1)残差大小的检验。对模型预测值和原始沉降数据序列逐点检验。

(2)后验差检验。它由后验差比值C和小误差概率P这两个指标来描述，主要对残差分布的统计特性进行检验，是灰色GM(1，1)模型精度检验最重要的评定方法。一般情况下，按照这两个指标将模型精度分为4个等级[7]，如表1所示。

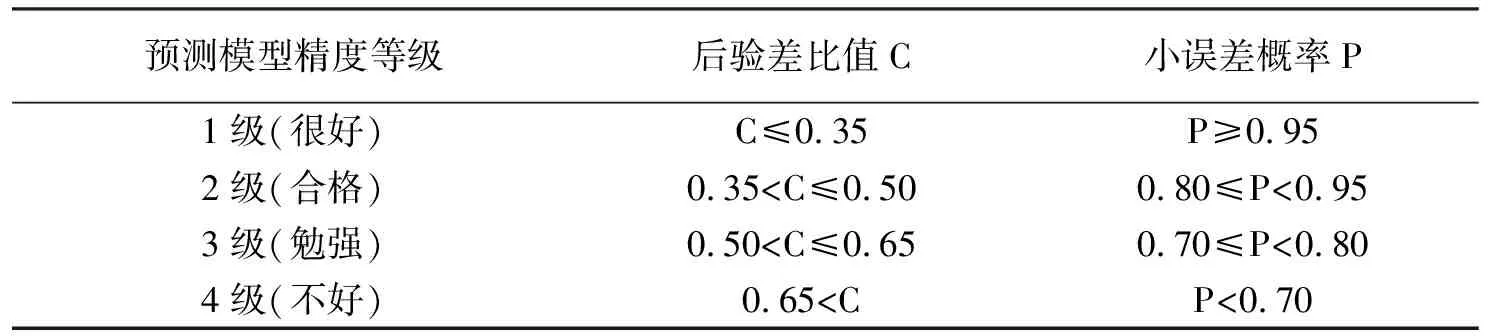
表1 检验样本数据表

4 应用实例

4.1 工程概况

路基某试验段DK0+240处地层为硬壳层厚3.6 m，软土层厚12.6 m，粘土层厚5 m，其下为粉砂。深层搅拌桩加固软土地基，加固深度15.5 m。在线路左侧、线路中心、线路右侧设置观测点，分别埋设3个沉降板。限于篇幅，选取线路左侧实测150～380 d的24组实测数据(见表2)作为原始沉降序列。线路中心线、线路右侧的预测方法与此相同。

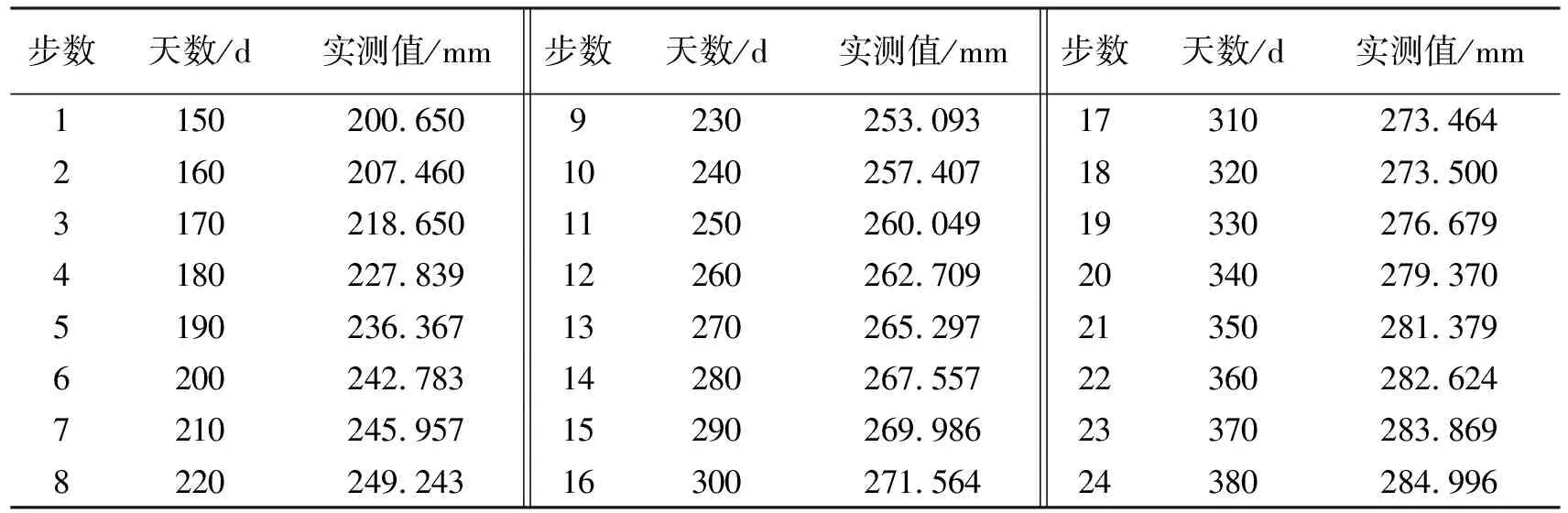
表2 线路左侧实测数据

4.2 预测模型精度检验

4.2.1 残差检验

为检验普通GM(1，1)模型和残差修正的GM(1，1)模型的拟合效果，将表2所示线路左侧实测150～380 d的24组实测数据作为原始沉降序列，分别用普通GM(1，1)模型和残差修正的GM(1，1)模型进行拟合预测。由于计算过程较为复杂，本文选用MATLAB编程求解。为进一步说明预测效果，将两种模型的预测值和实测值进行对比，并求出两种模型的相对误差。计算结果如表3和图1、图2所示。

表3 普通GM(1，1)模型和残差修正的GM(1，1)模型预测对比表

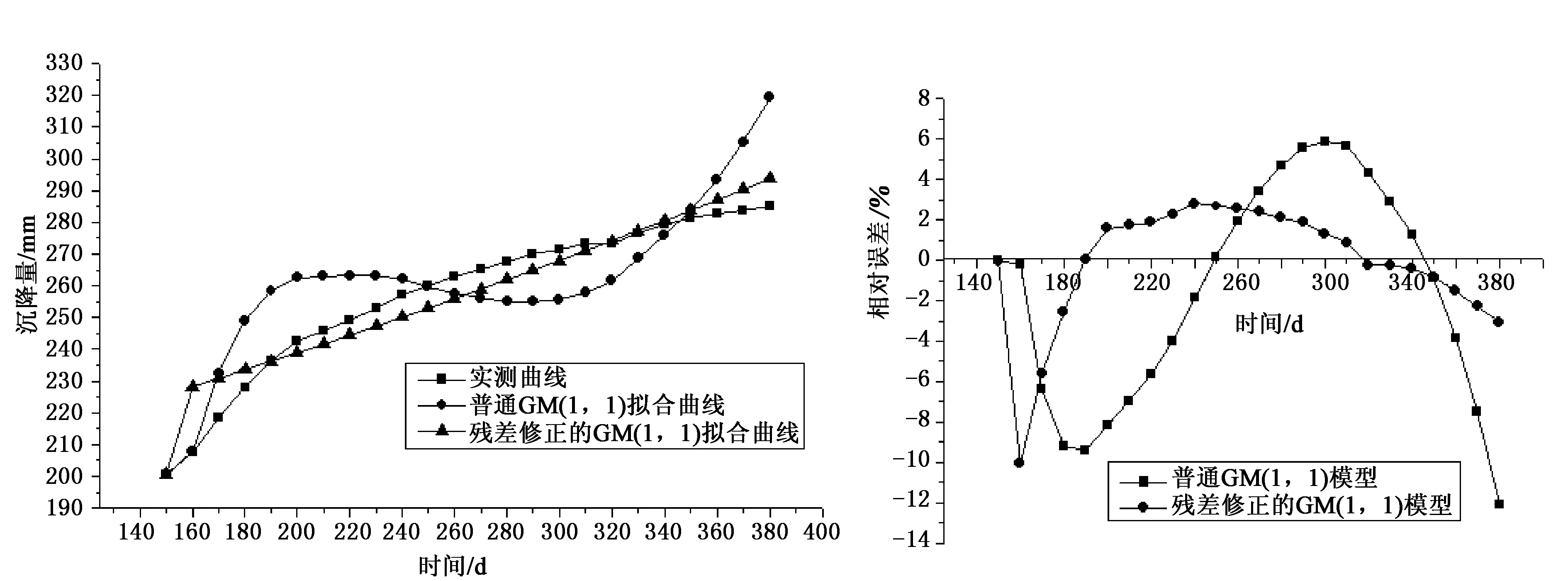
图1 模型拟合曲线与实测曲线对比图图2 模型拟合相对误差比较图

由表3和图1—2可知，普通GM(1，1)模型的拟合曲线与实测曲线吻合效果欠佳，最大相对误差为-12.07%，说明普通GM(1，1)模型用于路基沉降的预测虽是可行的，但有时误差会较大。而残差修正的GM(1，1)模型的拟合曲线与实测曲线基本完全吻合，除个别点可能是由于观测数据的原因使最大误差达到-10.05%和-5.62%外，其余最大误差仅为-3.04%，拟合效果较好。

4.2.2 后验差检验

后验差比值C和小误差概率P是灰色模型精度检验的两个重要指标。为进一步比较普通GM(1，1)模型和残差修正GM(1，1)模型的预测精度。通过编程将两个模型的后验差指标和精度比较结果列于表4。