考虑滤波环节寄生电阻的三相电压型逆变器的数学模型分析

董锋斌， 皇金锋， 侯 波， 边鹏江

(陕西理工学院 电气工程学院， 陕西 汉中 723000)

0 引 言

系统模型是系统本质属性的抽象描述，系统数学模型是用数学形式表示的输出对输入的响应关系，它是定量分析的基础，是设计反馈控制系统的基础。从控制理论的角度分析，要使一个系统实现更好地控制，必须建立其数学模型。三相三桥臂电压型逆变器是一种广泛应用于交流调速、不间断电源、感应加热电源、太阳能及风能发电等领域的功率变换器，如果能建立其合理的数学模型，对逆变器分析和闭环设计将具有十分重要的意义[1-4]。

就三相电压型逆变器系统主拓扑而言，主要是由多个全控型开关器件、二极管和滤波电感、电容等组成。由于开关存在开通和关断两种工作状态，导致三相电压型逆变器是一个变结构的系统，且开通时的电路拓扑和关断时的电路拓扑完全不一致，二极管、开关管又是非线性器件，一相桥臂上的开关导通与关断会对其它两相负载的电压产生影响，这些决定了三相电压型逆变器的电路本质是时变的、耦合的、多输入、多输出的非线性系统[1-3]。对这样一类系统，一般采用的建模方案总体上可分为两类，一类是数值法，一类是解析法。数值法主要用于计算机仿真， 解析建模方法主要包括：状态空间平均法和切换系统模型等。切换系统模型是从切换系统理论出发，建立了三相逆变器的切换系统模型，该模型能真实地反映逆变器的实际物理工作过程。对系统的稳定性分析有一定的作用，但是切换系统数学模型建立十分困难，且不具有一定的普遍性[4-5]。对设计闭环控制系统，人们更关心的是能正确地反映系统输入、输出之间基本关系的系统动态数学模型，因此空间平均法应用更为广泛[6-7]。

在文献[6]中，讨论过用状态空间平均法建立了三相电压型PWM逆变器的数学模型，并讨论了三相电压型PWM逆变器的开关周期平均数学模型和小信号交流模型，其模型中所带负载为阻性负载。文献中未讨论阻感性负载的工况情况，没有讨论为设计反馈控制系统所需要的从控制输入到逆变器输出的传递函数。在文献[8-9]中虽讨论过带阻感性负载的工况，但是在理想状况下，没有考虑滤波电容的电阻和滤波电感电阻。受文献[6]建模思路启发，本文对考虑寄生电阻的三相电压型逆变器进行了建模分析，建立了三相逆变器非理想工况下带阻感性负载的数学模型，并对这些寄生参数对系统频率特性的影响进行了讨论，得到了一些有用的结论，对三相电压型逆变器分析和闭环设计提供一些理论基础。

1 三相电压型逆变器的建模研究

三相电压型逆变器的拓扑如图1所示，skj为全控型电力电子开关，其中k∈{a,b,c},j∈{p,n}。Lf 1、Lf 2、Lf 3为滤波电感，Cf 1、Cf 2、Cf 3为滤波电容，r1、r2、r3是考虑滤波电感的等效串联电阻,rc1、rc2、rc3是滤波电容的等效串联电阻。实际应用中，一般三相参数基本对称，于是有Lf 1=Lf 2=Lf 3=Lf，Cf 1=Cf 2=Cf 3=Cf，r1=r2=r3=r，rc1=rc2=rc3=rc。zA=zB=zC为三相对称负载。虽然6个开关有64种组合，但为保证不造成电压源或电容的短路、电流源或电感的开路，逆变器仅有8种有效组合。任一瞬时每相中只有一个开关器件导通。定义相开关函数sk，k∈{a,b,c}，当sk=1时，表示与p相连，sk=0时，表示与n相连。相应线开关函数为sab=sa-sb，sbc=sb-sc，sca=sc-sa。依据6个开关的8种状态中直流侧、交流侧电量与开关函数之间的关系[6]和基尔霍夫定律可以得到：

(1)

图1 三相电压型逆变器电路拓扑

定义虚拟线电流iab=ia-ib，ibc=ib-ic，ica=ic-ia。由三相对称性可得：

(2)

依据基尔霍夫定律有

(3)

如果三相负载满足F(iA,uAB)=0，F(iB,uBC)=0，F(iC,uCA)=0，F(·,·)=0是随负载性质变化的隐函数方程。对A相有：

(4)

综合(1)、(2)、(3)和(4)式，有

(5)

由式(5)可以看出，模型中出现未知函数，不便做深入讨论。未知函数是由负载而定的，当负载一定时，模型中就不会出现未知函数，阻感性负载是一类典型的负载，这里以阻感负载为例，继续讨论模型分析。三相电压型逆变器带三相对称阻感负载的拓扑如图2所示。图中Lo为负载电感，Ro为负载电阻。

在图2中，根据基尔霍夫定律有：

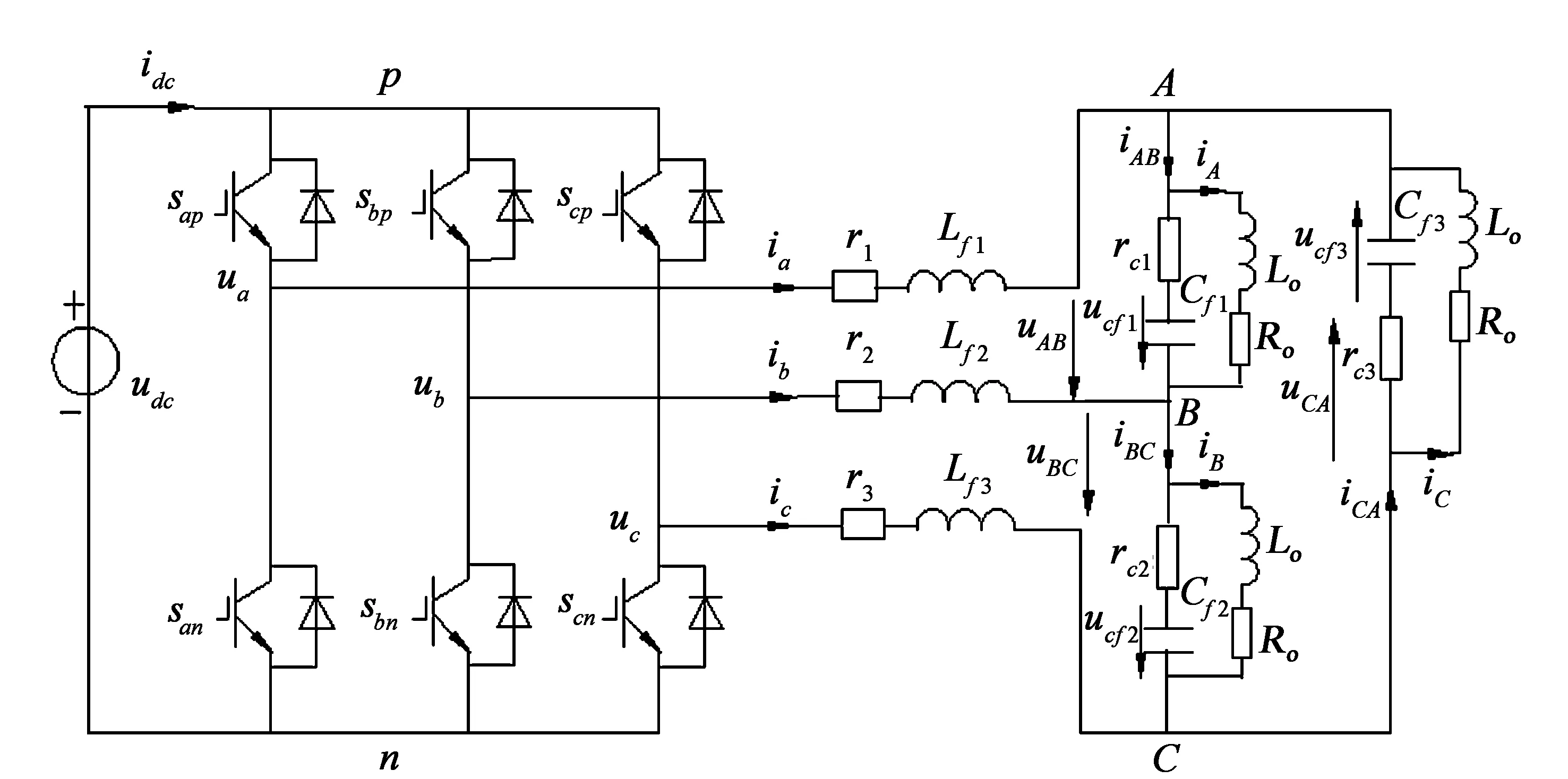
图2 三相电压型逆变器带阻感负载电路拓扑

(6)

将式(6)带入式(5)中，虽不会出现未知函数，但模型中存在不连续的开关函数，此系统为离散的，引入开关周期平均算子式(7)[7]，将系统变换成连续的系统，其中Ts为开关周期，x(t)为电路中的某电量,

(7)

一般有开关频率远大于电路中电量的变化频率，因此在一个开关周期内电感电流、电容电压和直流侧电压这些连续量变化较小，于是有如下近似关系：

(8)

对线开关函数求开关周期平均后，有

(9)

式中da为a相上桥臂开关管在一个开关周期的占空比，db为b相上桥臂开关管在一个开关周期的占空比。

定义线间占空比dab=da-db，dbc=db-dc，dca=dc-da，其取值范围在+1到-1之间。经开关周期平均后，有式(10)成立，其中除线间占空比外，其余各变量均保持原有书写格式:

(10)

公式(10)虽然较为准确地表征了系统中各个物理参数之间的约束关系，但对设计闭环控制系统，人们更关心的是能正确地反映系统输入、输出之间基本关系的系统动态数学模型，具体地说是从控制输入到逆变器输出的传递函数。从上式中可以看出，存在乘积项，系统为非线性的，利用拉普拉斯变换求解系统传递函数有一定的难度[10]。这里应用小信号扰动法来继续讨论系统模型。

将稳态值和扰动量代入式(10)，消去稳态值并忽略二阶无穷小量，可得

(11)

可以看出式(11)是一个线性系统的数学模型，取拉氏变换后，可得到如下的传递函数为(12)式：

(12)

其中传递函数的分子多项式和分母多项式分别为：

num=rcLoCfs2+(rcCfRo+Lo)s+Ro，

den= 3LfCfLos3+[3LfCf(Ro+rc)+(3r+rc)CfLo]s2+

[3rrcCf+(3r+rc)RoCf+3Lf+Lo]s+(3r+Ro),

当rc=0，r≠0，即忽略滤波电容的电阻时，传递函数的分子多项式和分母多项式分别变为：

num1=Los+Ro，

den1=3LfCfLos3+(3LfCfRo+3rCfLo)s2+(3rRoCf+3Lf+Lo)s+(3r+Ro),

当rc=0，r=0，即忽略滤波电容的电阻和滤波电感的电阻时，传递函数的分子和分母多项式分别变为：

num2=Los+Ro，

den2=3LfCfLos3+3LfCfRos2+(3Lf+Lo)s+Ro,

其模型和文献[8]中的结果一致。

从以上的建模过程知，对同一个系统有3种数学模型，包括式(5)的开关函数模型、式(10)的线间占空比函数模型和公式(12)的传递函数模型。其中开关函数模型未作任何假设，属于大信号数学模型。线间占空比函数模型是在忽略开关频率及其边频带、开关频率谐波及其边频带的条件下建立的低频大信号数学模型。传递函数模型是小信号数学模型。对于大信号模型，可以作为非线性控制方法的基础，而小信号模型则是采用经典控制理论的基础。

2 小信号数学模型分析

从输入到输出的传递函数为应用成熟的反馈设计提供了理论依据。但由于滤波电容的电阻和滤波电感的电阻在逆变器工作时不好测量，是否考虑这些因素，这些因素究竟对系统的分析和闭环设计有多大影响，这是工程设计人员所关心的，对其进行分析如下。

2.1 模型阶数

比较den、den1和den2，可以看出系统模型的阶数均为3阶，与忽略rc和r无关。考虑rc和r时，改变的是s2、s1和s0项前面的系数，s3项前面的系数不变。这说明系统模型的阶数与储能元件的种类与个数有关，而与是否考虑rc和r无关。

2.2 频率特性比较

为说明它们频率特性的差异，选择一组数据绘制其Bode图曲线进行比较[11]。一般Lf、Cf滤波器的转折频率为开关频率的1/10，通常状况下开关频率多半取到10 kHz以上，因此取1 kHz作为Lf、Cf滤波器的转折频率，对应可取Lf=1 mH和Cf=25 μF。其余参数为：r=1 Ω，rc=0.5 Ω，udc=400 V，Ro=20 Ω，Lo=0.5 mH。将上述参数带入式(12)中，以占空比输入到线电压输出的传递函数为例，得到：

利用MATLAB软件分别绘制其Bode图曲线[12]，如图3所示。

图3 Bode图曲线

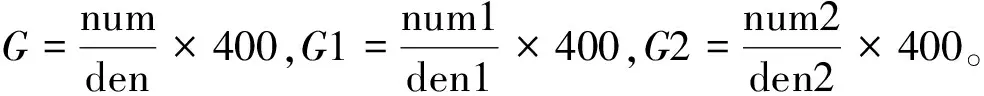
针对以下3种情况绘制不同的Bode图，得到如表1的数据：(1)设rc=0，r=0时系统频率特性；(2)设r≠0，只改变rc，分析其对系统频率特性的影响；(3)设rc≠0，只改变r，分析其对系统频率特性的影响。

表1 参数变化时频率特性信息

从表1中可以得到以下结论：

(1)当rc=0，r=0时，Bode图谐振峰值最大，相角裕度最小，系统稳定性最差，截止频率最小;

(2)当r≠0，随着rc增大，Bode图谐振峰值减小，相角裕度增大，系统稳定性增强，截止频率增大;

(3)当rc≠0，随着r的增大，Bode图谐振峰值减小，相角裕度增大，系统稳定性增强，截止频率在减小，但变化不大。

上述结论是在一组数据下得到的，如改变参数值仍有上述结论。

从以上分析可以得到：考虑滤波电容的电阻和滤波电感寄生电阻得到的数学模型能够更加准确地反映出逆变器的工作特性，但从控制的角度出发，不考虑寄生电阻的数学模型其系统稳定性最差。也就是说按照不考虑寄生参数的小信号数学模型来设计系统，实际上是按照最坏的情况下来设计闭环系统，设计出的调节规律能满足系统要求。

3 结 论

本文针对三相电压型逆变器这类耦合的、多输入、多输出的非线性系统，利用开关函数、开关平均算子等建立了其大小信号模型，得到了以下结论：

(1)大信号模型包含系统信息较为全面，但存在非线性项，可以作为非线性控制方法的基础；采用小信号扰动法建立的模型则可以作为经典线性控制方法的基础。

(2)考虑滤波电容的电阻和滤波电感电阻得到小信号数学模型的阶数，和不考虑寄生参数的小信号数学模型的阶数相同，说明系统模型的阶数与储能元件的种类与个数有关，而与是否考虑rc和r无关。

(3)从控制的角度出发，不考虑寄生电阻的数学模型，其系统稳定性最差。也就是说按照不考虑寄生参数的小信号数学模型来设计系统，实际上是按照最坏的情况下来设计闭环系统，设计出的调节规律能满足系统要求。

[参考文献]

[1] MIDDLEHROOLS R D, CULS S. A general unified approachto modeling switching converter power stages[C].IEEE PESC’76 Record, 1976: 18-31.

[2] YE Y, KAZERANI M, QUINTANA V H. A novel modelingand control method for three phase PWM converters[C].IEEE PESC’01, 2001(1): 102-107.

[3] YANG Y, KAZERANI M, QUINTANA V H. Modeling, control and implementation of three-phase PWM inverter[J].IEEE Transactions on Power Electronnics,2003,18(3):857-864.

[4] 李琼林,刘会金,宋晓凯,等.基于切换系统理论的三相变流器建模及其稳定性分析[J].电工技术学报，2009，24(11):89-95.

[5] 李建林，王立乔，熊宇，等.三相电压型变流器系统静态数学模型[J].电工技术学报，2004，19(7)：11-15.

[6] 徐德鸿.电力电子系统建模与控制[M].北京：机械工业出版社，2006:8-134.

[7] 张卫平.开关变换器的建模与控制[M].北京：中国电力出版社，2006:10-20.

[8] 董锋斌,皇金锋,钟彦儒.一种三相SPWM逆变器的建模和控制方法[J].电机与控制学报,2010,14(8):87-92.

[9] 董锋斌，皇金锋,傅周兴.一种三相四桥臂逆变器的数学模型分析[J].电力自动化设备，2011，31(6)：98-101.

[10] 吴麒，王诗宓.自动控制原理[M].2版.北京：清华大学出版社，2006:366-370.

[11] 薛定宇.控制系统仿真与计算机辅助设计[M].北京：机械工业出版社，2007:53-93.

[12] 楼顺天，姚若玉，冶继民.基于MATLAB 7.X的系统分析与设计[M].西安：西安电子科技大学出版社，2005:116-139.