圆度误差分离技术国内外研究现状与展望

张玉梅

（赤峰学院 建筑与机械工程学院，内蒙古 赤峰 024000）

圆度误差分离技术国内外研究现状与展望

张玉梅

（赤峰学院 建筑与机械工程学院，内蒙古 赤峰 024000）

介绍了圆度误差测量过程中主轴回转误差分离技术和误差分离原理，讨论了各种误差分离方法的优缺点和适用场合，分析了误差分离技术的发展趋势.

误差分离技术；反向法；多步法；多点法

在进行圆度误差测量时，传感器采集的圆度误差信号中，既包括圆度误差信号，也包括主轴回转误差.当主轴回转误差和圆度误差处于同一数量级时，会对圆度误差测量结果造成明显干扰，影响其测量精度，因此必须采用误差分离技术将其去除.根据测量过程中所用传感器数量及操作步骤，圆度误差分离技术可以分为：反向法[1-3]、多步法[4-6]及多点法[7-11].下面分别讨论分析.

1 反向法

反向法是一种比较简单的误差分离方法，出现相对较早[2,12].其误差分离原理如图1所示：首先，被测工件与主轴按图1（a）所示位置安装，传感器对被测工件做第一次测量，设所测信号为u；然后，被测工件相对主轴转过180°，如图1（b）所示，进行第二次测量，设所测信号为u'；最后，对两次测量数据进行处理，实现主轴回转误差与被测工件圆度误差的分离.

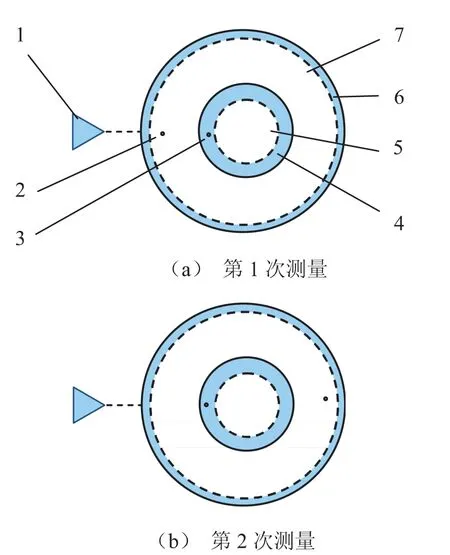
图1 反向法误差分离原理图

因测量信号中同时包含被测工件的圆度误差r和主轴回转误差h，所以两次测量结果可分别表示为：

将两组测量数据对应相减，即可分离掉主轴回转误差h，得到被测工件圆度误差r：

在具体测量时，反向法还有如下三种具体实施方式[3].（1）反向测量时，主轴位置不动，传感器和被测工件相对主轴转过180°.（2）反向测量时，传感器与主轴位置不动，被测工件相对主轴转过180°.（3）使用两个相隔180°的传感器，对工件两个方向同时进行测量.三种方法中方法（2）相对简单易操作.文献[3]对这三种反向法的测量精度进行了分析，发现：方法（1）所得圆度误差测量信号中会包含部分主轴误差；方法（2）可以完全消除主轴误差，但会丢失部分圆度信号；方法（3）所得圆度误差测量信号中既丢失了部分圆度误差信号，又混入了一些不需要的主轴回转误差信号.针对反向法存在的问题，文献[1]提出了改进反向法：采用两个传感器和一次反向测量来分离主轴回转误差.这种方法测量精度较高，对主轴回转精度和主轴回转误差的重现性要求不高.文献[2]对比分析了反向法和多步法的测量精度，证明反向法的测量精度达到了多步法的测量精度.文献[4]对比分析了反向法、多点法和多步法的测量精度，发现三种方法在高精度检测中，测量精度相近.

反向法的优点是操作简单，整个测量过程中一般只需一个传感器和一次反向定位操作，存在的问题是要求主轴回转精度较高.此方法适合于离线测量.

2 多步法

多步法，顾名思义，就是通过对被测工件不同相位进行多次测量来实现误差分离的一种测量方法.根据每次测量工件相对主轴转过的角度是否相同，多步法可以分为等转角测量和不等转角测量两种类型.

多步法使用一个传感器，在测量过程中，其位置始终不动，每测量一次，工件相对主轴转过一个角度.通过对所有测量数据进行处理，实现误差分离[5].其中等角度转位法测量原理如下[13]：

设圆度误差为ri（i=1,2,…,k，k为步数），主轴回转误差为ε，则测量数据si可表示为

设采用k步法进行测量，每次采样点数为N，则每步需转过N/k点，第i+1步测量的被测工件圆度误差可表示为r(iN/k).测量读数方程可表示为

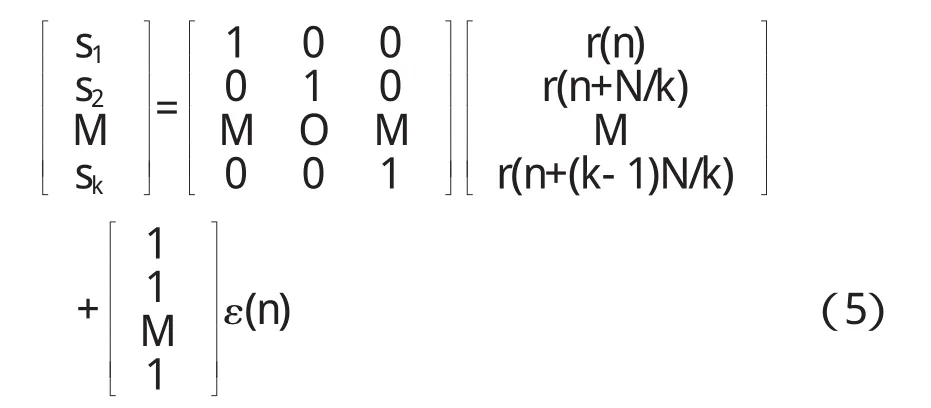
式中n为采样点序号，n=1,2,…,N.

用L=(l1,l2,…,lk)=(1，-1/(k-1),…,-1/(k-1))左乘式（5）两边，然后对所有读数求和，式（5）右边第2项为

则式（5）左边读数和S(n)为

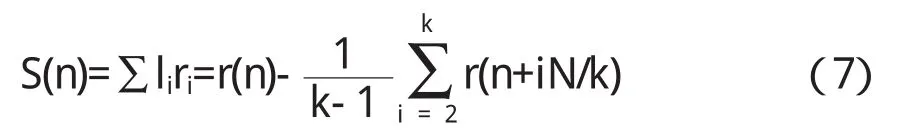
对式（7）作傅立叶变换，得圆度误差频域表达式R(m)

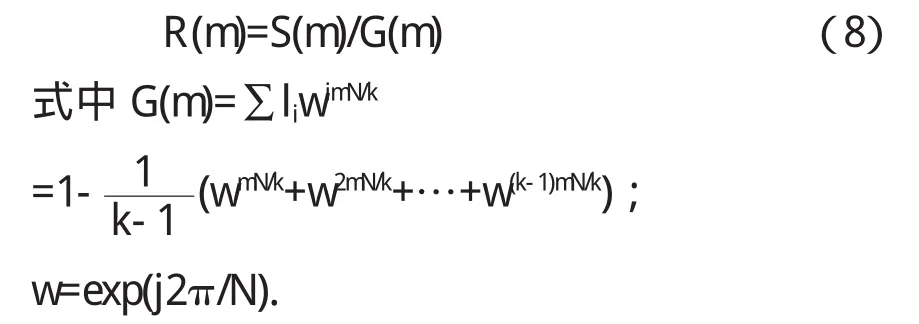
对式（8）作傅立叶逆变换，即可消去主轴回转误差，得圆度误差为

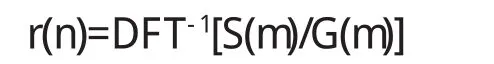
多步法因为只使用一个传感器，所以从传感器的角度讲，系统的稳定性比较好.但是当谐波次数等于测量步数整数倍时，会出现谐波抑制，减少谐波抑制的方法是提高转位次数，但又影响测量效率，而且因测量时间增长而会增加检测系统的稳定性[14].多步法测量精度与转位精度密切相关，要求每步测量的起始点要严格控制[6].综上，多步法比较适合离线测量[7,13].不等转角多步法是指每步转过的角度不同，如果转位角度选择合理，只需两步就能有效分离主轴回转误差.

3 多点法

所谓多点法，是指使用多个传感器同时对工件进行测量，通过对多组采样数据进行处理来分离主轴回转误差的测量方法.常用有三点、两点及四点法[15].

（1）三点法.多点法中使用最多[8]，而且JB/T5996-1992中有详细的使用规定[16]，其误差分离原理为：

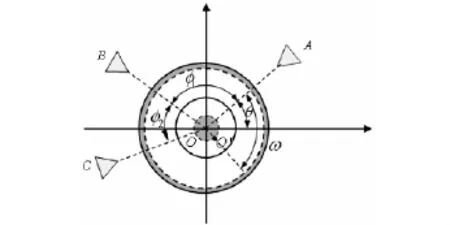
图2 三点法误差分离原理图

传感器A、B、C间隔一定角度沿被测截面周向排列安装（如图2所示），测量方向为工件径向.工件与主轴同步转动，在回转一周的过程中，三个传感器从不同相位对被测轮廓进行测量.

设三传感器测量数据分别为S1(θ)、S2(θ)和S3(θ)，则

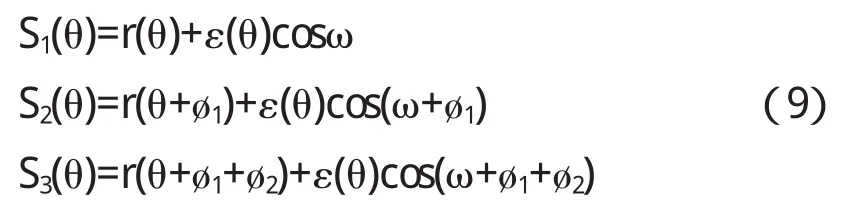
式中r(θ)——被测截面圆度误差信号；

ε(θ)——主轴回转误差信号；

θ——传感器初始相位角；

ø1，ø2——传感器间隔角度；

ω——回转中心O'的初始相位角.

取传感器A、B、C的影响系数分别为C1、C2、C3，且让

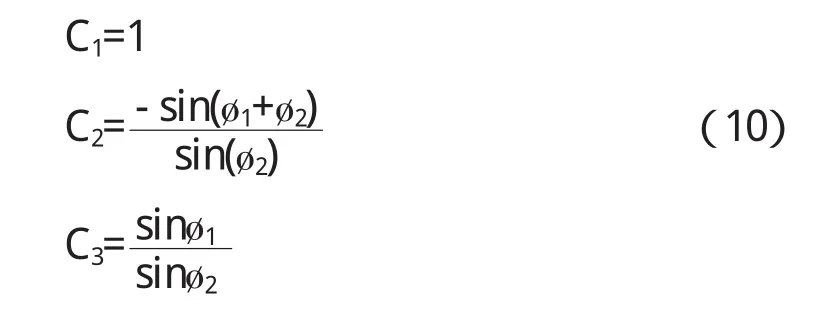
用式（10）中的C1、C2、C3与传感器A、B、C的读数方程分别相乘然后等式两边求和，得到圆度误差的测量方程：

对式（11）作傅立叶变换和逆变换，即可分离掉主轴回转误差，得到被测截面轮廓的圆度误差r(θ).

由于测量系统的原理性问题，常规三点法存在谐波抑制问题.为减小谐波抑制对测量精度的影响，文献[17]提出了混合三点法——采用一个广义位移传感器和一个线位移传感器的方法，广义传感器中含有一个角位移传感器和一个线位移传感器，通过合理设置传感器间隔角度，可以有效降低谐波抑制，提高圆度误差测量精度.当被测轮廓上有突变点时，在数据处理过程中会出现信号失真而影响测量效果，针对这个问题，文献[7]提出了联合三点法，即等角度间隔安装传感器的方法与不等角度间隔安装传感器的方法相结合的方法.实验结果证明对于有突变点的轮廓，联合三点法可以有效提高测量精度.文献[10]针对文献[7]，又提出了两点改进措施：一、根据预测数据选择传感器安装角度，可进一步提高测量精度和测量范围；二、用limacon曲线代替常用二次曲线.针对常规三点法传感器定位难和数据计算量大的问题，文献[18,19]提出了平行三点法，简化了传感器的定位操作，提出了数据时域解法，节省了计算用时.文献[11,20-22]研究分析了三点法测量精度的影响因素.

3.2 两点法

使用两个传感器同时进行圆度误差测量的方法.文献[14]提出，用两点法进行测量之前，要先对两传感器进行性能补偿，减小两传感器的差异，以提高测量精度.文献[23]针对在线测量的情况，提出了改进两点法，节省了安装空间，并能用于曲轴的圆度误差测量.文献[24]研究并实现了用两点法来测量超精密车床主轴回转误差.文献[9]提出了混合正交两点法，解决了三点法安装困难的问题.

3.3 四点法

即采用四个传感器对被测轮廓同时进行测量来分离主轴回转误差的方法.针对三点法中存在的谐波抑制问题，文献[25]研究了四点法、五点法以及n点法，实验证明冗余测量数据可以降低传感器读数误差和定位误差对测量精度的影响，但是当传感器数量多于四个以后，对测量精度的改善效果就不再明显，由此说明四个传感器属于最佳配置数量.文献[26,27]研究了用四点法测量圆度误差和主轴回转误差，并证明四点法比三点法谐波抑制情况有改善.

综上，多点法只需一次测量，就可以分离主轴回转误差，因此更适合在线测量.但是多点法中多个传感器的安装比较困难，而且，为提高系统的稳定性和测量精度，要求传感器间差异性要小，同时，多个传感器，意味着成本的增加.

4 结论

综上所述，各种误差分离方法各有利弊，不论哪种方法，只要设计合理，都能有效分离主轴回转误差，提高圆度误差测量精度.根据上述各种方法的特点，，可以预测误差分离技术的发展趋势：一，离线测量时，优先考虑多步法.重点是研究如何减小测量步数和重新准确定位的方法，以提高效率，减小因重新定位而带来的不利影响；二，在线测量时，使用多点法.重点是研究多个传感器的合理相对位置关系和各传感器的简单准确安装定位方法.总之，先进的误差分离技术，对提高加工精度、保证产品质量有重要意义.

〔1〕Horikawa O.,Maruyama N.,Shimada M.A low cost,high accuracy roundness measuring system[J].Precision Engineering,2001,25(3): 200-205.

〔2〕Eric R Marsha,David A Arneson,Donald L.M artin.A comparison of reversal and multiprobe error separation[J].Precision Engineering, 2009,20(2):161-166.

〔3〕曹麟祥,谢会崇,胡签,等.反向法误差分离技术的测量精确度[J].计量学报,1985,6(4):269-273.

〔4〕Eric marsh,Jerem iah couey,Ryan vallance. Nanometer-level comparison of three spindle error motion separation techniques[J].Manufacturing Science and Engineering,2006,128(1): 180-187.

〔5〕雷贤卿,李言,李济顺,等.多步法圆度误差分离的演化形式及谐波抑制分析[J].工业仪表与自动化装置,2006（1）:45-46.

〔6〕叶京生,顾启泰,章燕申.论多步法误差分离技术的测量精度[J].计量学报,1990,11(2):119-123.

〔7〕Wei Gao, Satoshi Kiyono. On-machine roundness measurement of cylindrical workpieces by the combined three-point method[J]. Measurement,1997,21(4):147-156.

〔8〕Wei Gao,Satoshi Kiyono.High accuracy profile measurement of a machined surface by the combined method[J].M easurement,1996,9(1): 55-64.

〔9〕W ei Gao,Satoshi Kiyono,Takam itu Sugawara. High-accuracy roundness measurement by a new error separation method[J].Precision Engineering,1997,21:123-133.

〔10〕Muralikrishnan B.,Venkatachalam S.,Rajaa J., et al.A note on the three-point method for roundness measurement[J].Precision Engineering,2005,29:257-260.

〔11〕Jay F.Tu,Bernd Bossmanns,Spring C.C. Hung.Modeling and error analysis for assessing spindle radial error motions[J].Precision Engineering,1997,21:90-101.

〔12〕R.R.Donaldson.A simple method for separating spindle error from test ball roundness error[J].Ann.CIRP.,1972,21(1):125–126.

〔13〕洪迈生,蔡萍.多步法误差分离技术的比较分析[J].上海交通大学学报,2004,38(6):877-881.

〔14〕陈永当,李少康.圆度测量误差分离方法[J].西安工业学院学报,2000,20(4):327-333.

〔15〕张玉金.实现主轴回转误差完全分离的理论和技术[J].现代计量测试,2002,10(3):25-27.

〔16〕JB/T5996－1992,圆度测量三测点法及其仪器的精度评定.中华人民共和国机械电子工业部. 1992.

〔17〕W ei Gao,Satoshi Kiyono,Tadatoshi Nomura. A new multiprobe method of roundness measurements[J].Precision Engineering,1996,19: 37-45.

〔18〕洪迈生,邓宗煌,陈健强,等.精确的时域三点法圆度误差分离技术 [J].上海交通大学学报, 2000,34(10):1317-1319.

〔19〕洪迈生,魏元雷，苏恒，等.三平行传感器式频域法误差分离技术——在线测量圆度误差的新方法[J].仪器仪表学报,2003,24(2):152-156.

〔20〕魏元雷,洪迈生,苏恒,等.平行三点法圆度误差分离技术的精度分析 [J].机械科学与技术, 2003,22(1):51-54.

〔21〕张宇华,王晓琳,张国雄,等.测头读数及定位误差对三点法圆度测量精度的影响[J].中国机械工程,l999,10(5):534～537.

〔22〕Estler W.Tyler,Evans Chris J.,Shao L.Z. Uncertainty estimation for multiposition form error metrology [J].Precision Engineering, 1997,21(21):72-82.

〔23〕张邦成,杨晓红,吴狄,等.两点法在曲轴圆度误差测量中的应用 [J].现代制造工程,2005（6）: 75-77.

〔24〕黄长征,李圣怡,朱昱.超精密车床主轴回转精度动态测试机构的研制[J].航空精密制造技术, 2002,38(2):8-10.

〔25〕张宇华,王晓琳,张国雄,等.多点法圆度及轴系误差分离方法的若干问题[J].北京理工大学学报,1996,19(3):309-313.

〔26〕Zhang G.X.,Wang R.K.Four-point method of roundness and spindle error measurements [J].M anufacturing Technology,1993,42(1): 593-596.

〔27〕Zhang G.X.,Zhang Y.H.,Yang S.M.,et al. A multipoint method for spindle error motion measurement[J].CIRP Annals-Manufacturing Technology,1997,46(1):441-445.

TB92

A

1673-260X（2014）01-0129-04

本文系贵州省教育厅高校人文社会科学研究项目：《贵州省高校少数民族大学新生适应问题及对策研究》的阶段性成果之一（12FDY0160）