复变函数积分在复习总结中的教学研究

袁五届，周建芳，张金锋，尹新国

（淮北师范大学 物理与电子信息学院，安徽 淮北 235000）

复变函数积分在复习总结中的教学研究

袁五届，周建芳，张金锋，尹新国

（淮北师范大学 物理与电子信息学院，安徽 淮北 235000）

复变函数积分一直是复变函数论课程教学的重点和难点.结合多年的教学经验，本文以积分路径的封闭性和函数的解析性为理论分析的突破口，系统地归纳、总结了各种积分类型所采用的计算理论和计算方法，并辅助以恰当的例题来加深理解.本文的研究，将对学生牢固地掌握复变函数积分计算具有一定的指导作用，对教师进行系统的复习教学也具有一定的参考价值.

复变函数积分；柯西定理；柯西公式；留数定理

1 引言

复变函数论目前已形成完美的理论体系，成为一门非常重要的数学分支[1,2]，是解决当今许多理论和实际问题的强有力的数学工具[3,4]，其中复变函数积分是复变函数论中重要的核心内容之一.复变函数积分因其丰富的理论体系和众多的计算方法，使其一直是复变函数论这门课程教学的重点和难点，学生在掌握积分的理论以及恰当地选择积分的计算方法上都存在一定的难度.在目前的一些教材中，复变函数积分的理论和计算方法都不集中于某一章，众多的计算方法都是对于某种特殊类型的复变函数积分进行运算的，这就使学生很难系统地掌握这种复变函数积分的计算.因此，在教学复习中，对复变函数不同积分类型的计算理论和计算方法进行系统的归纳和总结就尤为重要.结合自己多年的教学经验，本文以积分路径的封闭性和函数的解析性为理论分析的突破口，系统地总结了复变函数积分常用的计算方法，对每种类型的复变函数积分及其不同的积分方法都辅助以适当的例题来加深理解.

2 复变函数积分类型及其计算方法举例

复变函数积分可以分为三种类型：带有上下限的定积分、非闭合曲线积分、闭合曲线积分.下面对这三种积分类型分别介绍相应的方法，并给予具体的实例.

2.1 带有上下限的定积分

这里可以采用牛顿-莱布尼茨公式进行计算，被积函数为初等复变函数的，可以根据相应的初等实函数来找出被积函数的原函数.

解 由牛顿-莱布尼茨积分公式，得

2.2 非闭合曲线积分

该类型的解题思路是化复变函数积分为实函数积分，可以根据具体形况采用如下两种方法.

2.2.1 参数积分法

如果积分曲线l可表示为参数方程z=z(t),其中a≤t≤b,则

2.2.2 化为实函数曲线积分法

若z和f(z)可分别表示为z=x+iy和f(z)=u(x,y)+iv(x,y),则

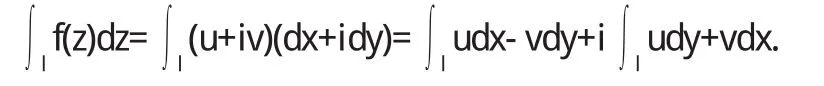
因此，可通过计算两个实函数曲线的积分来得到复变函数积分.

所以，两实函数的曲线积分均与积分路径无关[5]，可令两特殊积分路径线段：坐标原点到1点和1点到1+i点，有

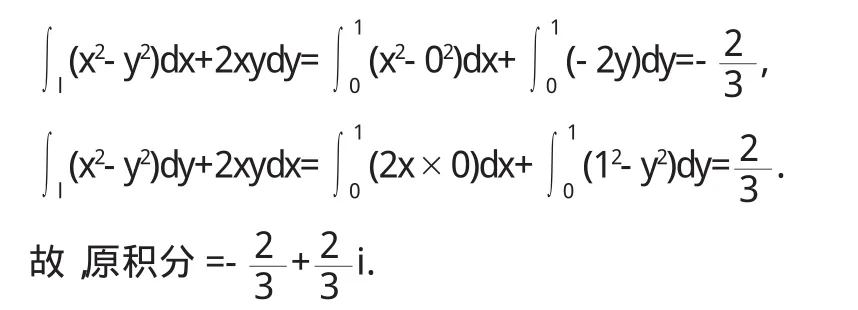
2.3 闭合曲线积分

此积分类型又称围线积分，该积分类型完全可以采用上述非闭合曲线积分的两种积分法：参数积分法和化为实函数曲线积分法.由于积分围线的闭合特性，这种积分类型又有其特殊的积分方法，以闭合曲线的积分方向为逆时针为例（若为顺时针积分方向，则积分值为逆时针方向积分的负值），解题程序的流程图如下：

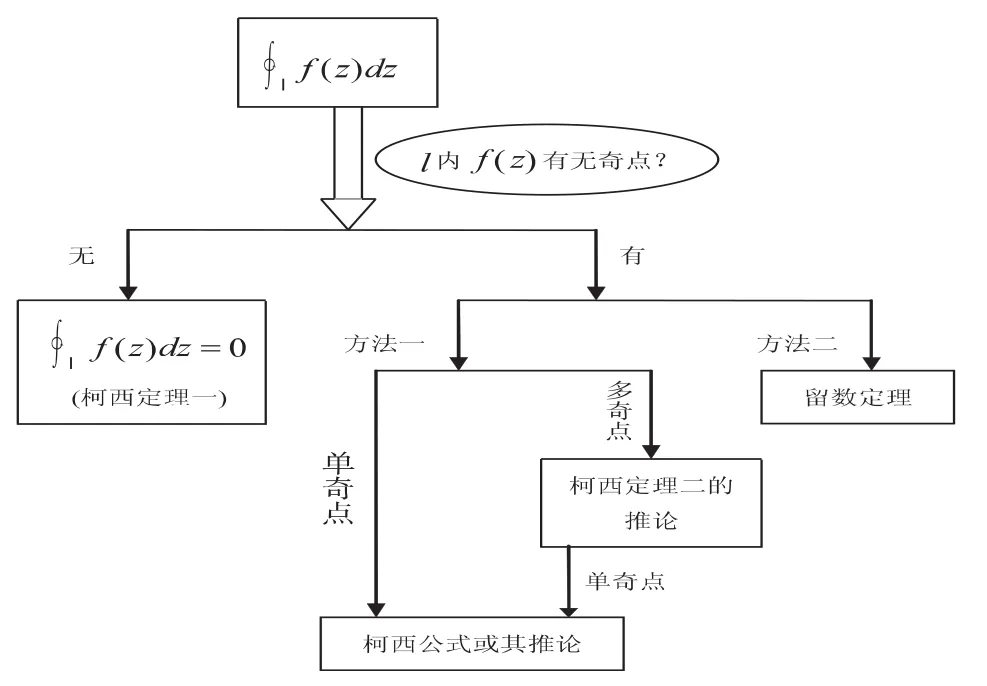
图1 求解闭合曲线逆时针方向积分的流程图

该流程图表明，对于闭合曲线的积分计算，要因题而异，下面分别对流程图中的各种情况加以举例.

所以，由柯西定理一得到：原积分=0.

例6

3 总结

复变函数积分计算，方法灵活多样，方法的选择要因题而异.对于不同的积分类型，一般的计算方法和思路可概括如下：对于含有上下限的定积分，先找出被积函数的原函数，然后利用牛顿-莱布尼茨公式计算（见例1）；对于非闭合曲线的积分，可化复变函数积分为实函数积分，一般采用两种方法，若积分曲线可表示为一元函数的参数方程，则利用参数积分法比较简便（见例2），否则，采用化为实函数曲线积分法来计算（见例3）；对于闭合曲线的积分，该积分类型完全可以采用上述非闭合曲线积分的两种方法，由于积分围线的闭合特性，这种积分类型有其特殊的积分方法（见图1），首先判断被积函数在积分围线内有无奇点，若无奇点，则由柯西定理一得到积分值为0（见例4），若有奇点，可以采用两种方法来计算，方法一为利用柯西公式或其推论（见例5、6的方法一），方法二为利用留数定理（见例5、6的方法二），其中，若只有一个奇点，可直接利用柯西公式或其推论计算（见例5的方法一），若有多个奇点，可先根据柯西定理二的推论化为积分围线内有一个奇点的积分类型，然后再根据柯西公式或其推论计算（见例6的方法一）.

为了学生能够系统地掌握复变函数积分的计算，在讲授完复变函数积分的各种理论和方法之后，教师要及时地对复变函数不同积分类型的计算理论和计算方法进行系统的归纳和总结，并辅助于典型例题，安排一到两个课时对学生集中复习.本文的研究，将对学生牢固地掌握复变函数积分计算具有一定的指导作用，对教师进行系统的复习教学也具有一定的参考价值.

〔1〕王文鹏，厥建华.复变函数积分的求解策略[J].重庆科技学院学报（自然科学版），2007，9（4）：145-147.

〔2〕胡嗣柱，倪光炯.数学物理方法（第二版）[M].高等教育出版社，2002.1-175.

〔3〕黄隽.复变函数积分计算方法的探讨[J].常州工学院学报，2008，21（4）：73-75.

〔4〕杨静宇.复变函数积分中值定理[J].赤峰学院学报（自然科学版），2010，26（5）：3-4.

〔5〕陈文灯，黄先开.数学复习指南（理工类）[M].世界图书出版公司，2001.293-294.

G642.0

A

1673-260X（2014）01-0-003-02

国家自然科学基金（11005047）；安徽省高校青年教师基金（2008jql071）；淮北师范大学青年基金（2013xqz17）；淮北师范大学教研项目（jy13234）；安徽省高等学校质量工程项目-物理学（师范）特色专业建设点(2011248)