线性方程组的迭代和最速下降法
2014-03-23刘盎然
刘盎然
(内蒙古大学 数学科学与技术学院,内蒙古 呼和浩特 010010)
线性方程组的迭代和最速下降法
刘盎然
(内蒙古大学 数学科学与技术学院,内蒙古 呼和浩特 010010)
本文在第一部分对迭代法进行了较为详细的描述.当遇到复杂问题时,特别是在未知量很多,方程为非线性时,我们无法找到直接解法,这时候或可以通过迭代法寻求方程的近似解.在可以用迭代算法解决的问题中,至少存在一个直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量.所谓迭代关系式,指如何从变量的前一个值推出其下一个值的公式(或关系).迭代关系式的建立是解决迭代问题的关键,可以用递推或倒推的方法来完成.在什么时候结束迭代过程,不能让迭代过程无休止地重复执行下去.迭代过程的控制可分为两种情况:一种是所需的迭代次数是个确定的值,可以构建一个固定次数的循环来实现对迭代过程的控制;另一种是所需的迭代次数无法确定,需要进一步分析出用来结束迭代过程的条件.第二部分是基于最速下降法在解决无约束非线性规划问题中的重要性,对其原理与算法予以讨论.
线性方程组;迭代法;最速下降法;最优解
1 基本定义与迭代法
1.1 向量序列与矩阵序列的收敛性
定义1.1.1设{x{k}}为Rn中的向量序列,x∈Rn,
其中||x(k)-x||为Rn中的向量范数,则称序列{x{k}}收敛于x,记为
其中x(k)=(x1(k),x2(k),…,xn(k)),x=(x1,x2,…xn)
定义1.1.3设{A{k}}为n阶方阵序列,A为n阶方阵,
其中||A(k)-A||为矩阵范数,则称序列{A{k}}收敛于A,记为
1.2 迭代法的一般形式
Ax=b⇔x=Mx+g其中A,M为n阶方阵,x,g∈Rn
迭代公式:xk+1=Mxk+g k=0,1,2,…,M为迭代矩阵,{x(k)}为迭代序列.
结论:若迭代公式x(k+1)=Mx(k)+g产生的迭代序收敛于x,则必有x=Mx+g,即为方租组Ax=b的解.
1.3 雅可比(Jacobi)迭代法
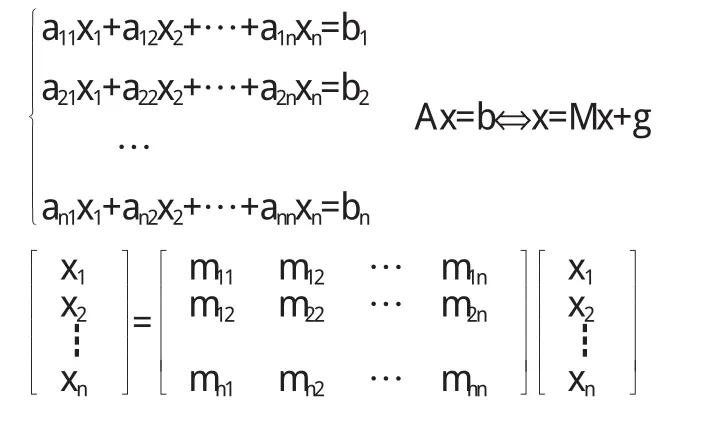

选取初始向量x(0),按以上公式产生的迭代序列成为Jacohi迭代(简单迭代法)Jacobi迭代法的矩阵形式:x(k+1)=Bx(k)+g
1.4 高斯-赛德尔(Gauss-Seidel)迭代法

2 迭代法基本收敛判别
2.1 迭代法收敛性理论
2.1.1 收敛性问题


2.1.2 收敛性基本定理
迭代法收敛性基本定理:设方程组为x=Bx+f对任意的初始向量x(0),解此方程组的迭代法x(k+1)=Bx(k)+f(k=0,1,2,…)收敛的充分必要条件是迭代矩阵B的谱半径ρ(B)<1
注意:此定理为判断迭代法的敛散性提供了一个强有力的手段(充分必要条件).然而,定理的条件往往不容易验证.因此,利用特征值上界性质ρ(B)≤||B||,可以给出另一个条件较弱的结果.
迭代法收敛性充分条件:如果迭代法x(k+1)=Bx(k)+f(k=0, 1,2,…)的迭代矩阵B的某一种算子范数||B||≤1,则
(1)对任意的初始向量x(0),迭代法收敛;
(2)迭代序列与方程组的解x*存在误差估计式

2.2 迭代法的收敛条件
2.2.1 矩阵的谱半径
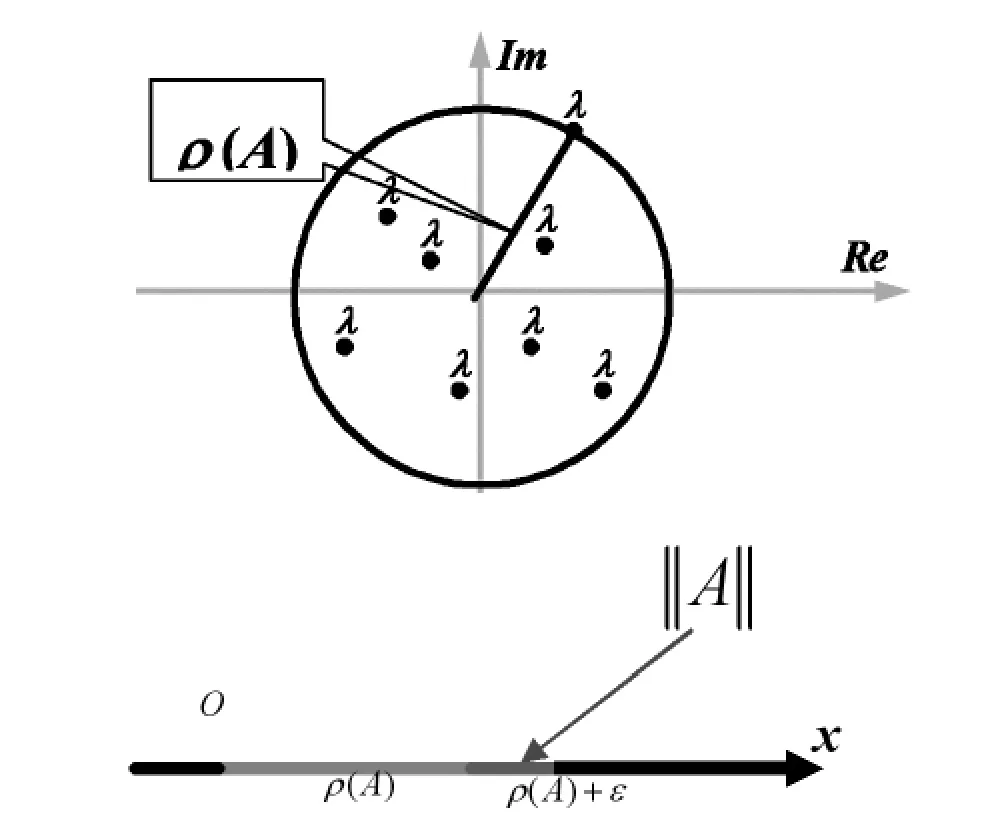
定义3.2.1设A为方阵,λi(i=1,2,…,n)为A的特征值,称特征值模的最大值为矩阵的谱半径,记为:

结论
1、ρ(Ak)=[ρ(A)]k
2、ρ(A)≤||A||,
其中||·||为任意由向量范数诱导出的矩阵范数;
3、∀ε>0,存在一种矩阵范数,使得||A||≤ρ(A)+ε,

2.2.2 迭代法的收敛条件定理与结论
定理 对任意初始向量x(0)
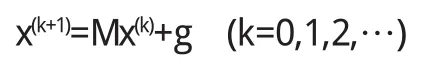
产生的向量序列{x(k)}收敛的充要条件是:ρ(M)<1
推论1在定理的条件下,若||M||<1,则对任意初始向量x(0),{x(k)}收敛.
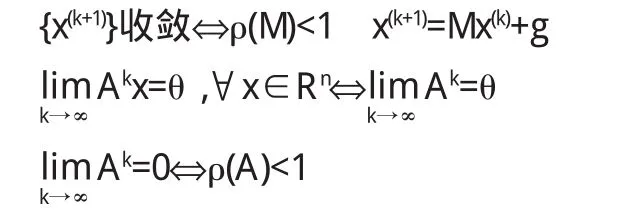
定义1若n阶方阵A=(aij)满足

且至少有一个i值,使上式不等号严格成立,则称A为纺对角占优阵.若对所有i,上式中不等号均严格成立,则称A为严格对角占优阵.不可约矩阵.

其中A11、A22为方阵,则称矩阵A不可约.
如下列矩阵

结论:设A=(aij)为n阶矩阵(n≥2),若存在非空集合I⊂{1,2,…,n},使得当i∈I,而i∉I时,有aij=0,则A是可约阵.
若A没有零元素,则A不可约.n=3时,A只有一个零元素,A不可约.
判别收敛的条件:
若A为严格对角占优阵或不可约弱对角占优阵,则Jacobi迭代法与G-S迭代法收敛.
注:常用条件直接对系数矩阵A判别.
1、先观察系数矩阵A是否对称正定或对角占优.
2、是否可以通过同解变形使系数矩阵具有上述特性(例如:交换方程的位置等)
3、给出迭代公式,讨论迭代矩阵的谱半径.
3 最速下降法
3.1 无约束问题的最优性条件
无约束问题的最优解所要满足的必要条件和充分条件是我们设计算法的依据,为此我们有以下几个定理.
定理4.1设f:Rn→R1在点∈Rn处可微.若存在p∈Rn,使
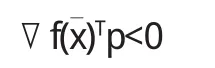
定理4.2设f:Rn→R1在点x*∈Rn处可微.若x*是无约束问题的局部最优解,

由数学分析中我们已经知道,使▽f(x)=0的点x为函数f的驻点或平稳点.函数f的一个驻点可以是极小点;也可以是极大点;甚至也可能既不是极小点也不是极大点,此时称它为函数f的鞍点.以上定理告诉我们,x*是无约束问题的的局部最优解的必要条件是:x*是其目标函数f的驻点.
定理4.3设f:Rn→R1在点x*∈Rn处的Hesse矩阵▽2f (x*)存在.若▽f(x*)=0,并且▽2f(x*)正定,则x*是无约束问题的严格局部最优解.
一般而言,无约束问题的目标函数的驻点不一定是无约束问题的最优解.但对于其目标函数是凸函数的无约束凸规划,下面定理证明了,它的目标函数的驻点就是它的整体最优解.
定理4.4设f:Rn→R1,x*∈Rn,f是Rn上的可微凸函数.若有
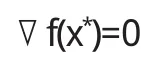
则x*是无约束问题的整体最优解.
3.2 最速下降法的基本思想和迭代步骤
最速下降法的基本思想是:从当前点xk出发,取函数f (x)在点xk处下降最快的方向作为我们的搜索方向pk.由f(x)的Taylor展式知
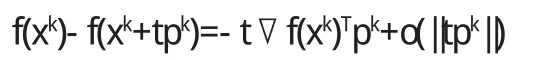
略去t的高阶无穷小项不计,可见取pk=-▽f(xk)时,函数值下降得最多.于是,我们可以构造出最速下降法的迭代步骤.
解无约束问题的的最速下降法计算步骤:

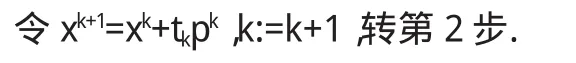
由以上计算步骤可知,最速下降法迭代终止时,求得目标函数驻点的一个近似点.
例1 minf(x)=x1-x2+2x12+2x1x2+x22给定初始点X(1)=(0,0)T

3.3 最速下降法的缺点
由于沿负梯度方向目标函数的最速下降性,很容易使人们误认为负梯度方向是最理想的搜索方向.必须指出的是,某点的负梯度方向,通常只是在该点附近才具有这种最速下降的性质.
在一般情况下,当用最速下降法寻找极小点时,其搜索路径呈直角锯齿状(图1-3),开始时目标函数下降较快;但在接近极小点时,收敛速度就不理想了.特别适当目标函数的等值线为比较扁平的椭圆时,收敛就更慢了.
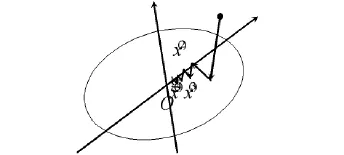
因此,在实用中常将最速下降法和其他方法联合应用.
在接近极小点时,可改用收敛较快的其他方法.
3.4 最速下降法程序流程图
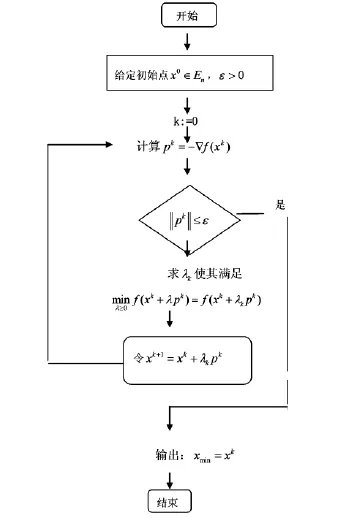
接触最速下降法1847年由著名数学家Cauchy给出的,它是解析法中最古老的一种,其他解析方法或是它的变形,或是受它的启发而得到的.
〔1〕黄明游.数值分析[M].高等教育出版社,2008.
〔2〕封建湖,车刚明,聂玉峰.数值分析原理[M].科学出版社,2005.
〔3〕关治,陆金甫.数值分析基础(第二版)[M].高等教育出版社,2010.
〔4〕Kendall Atkinson,韩谓敏.数值分析导论(第三版)[M].人民邮电出版社,2009.
〔5〕何汉林,梅家斌.数值分析[M].科学出版社,2009.
O241.6
A
1673-260X(2014)01-0010-04
