量子力学虚拟实验教学

2014-03-23谢勇

大理大学学报 2014年12期

谢勇

（大理学院工程学院，云南大理 671003）

量子力学研究的主要对象是波函数，而波函数的统计特性使得量子力学不能像经典物理学那样，体系的测量不会改变它的状态，它只有一种变化并按运动方程演进，运动方程对决定体系状态的力学量做出确定的预言〔1〕。量子力学的数学应用、符号运算和矩阵运算都十分抽象，所以量子力学的教学一直是我们不断总结和探讨的问题。为了能有效提高量子力学的教学效率，有的学校采用了一些现代化的辅助教学措施〔2-3〕，部分学校做了一些教学模式、教学方法改革的尝试〔4-6〕，均取得一定的效果。我们也采用过一些辅助措施来改进量子力学的教学〔7-8〕，但学生除了参与有限的课堂教学互动以外，就只能被动地去学习，不利于调动学生学习的积极性。近两年，我们利用Mathematica和Matlab两个平台，为我校物理本科专业的学生开设了量子力学的虚拟实验课，取得了一定的收效。本文将从量子力学的虚拟实验平台和量子力学虚拟实验设计方面介绍我们的教改思路和教改实践，以期能对同行的教学提供一个参考。

1 量子力学的虚拟实验平台

能够实现虚拟实验的平台比较多，如远程网络系统，局域网络系统和单机系统等等。由于我们的虚拟实验是在单机上完成的，所以我们重点对单机虚拟实验的设计平台进行了比较研究。针对我校物理专业本科学生的实际，我们选择了Matlab 和Mathematica两个平台。

1.1 Matlab 平台经过不断的系统更新，Matlab 已经从最初的实现程序库接口功能发展成为现在的将高性能的数值计算和可视化集成在一起的大型数学计算软件，已被广泛地应用于科学计算、控制系统、信息处理等领域的分析、仿真和设计工作〔9〕。Matlab的语法简单，编写容易，而且我校物理本科专业的学生在二年级就选修过Matlab，对软件有一定的了解，所以我们选择了部分量子力学的虚拟实验在Matlab上完成。

1.2 Mathematica 平台Mathematica 是一款科学计算软件，很好地结合了数值和符号计算引擎、图形系统、编程语言、文本系统，以及与其他应用程序的高级连接。很多功能在相应领域内处于世界领先地位，它也是迄今为止使用最广泛的数学软件之一。

Mathematica拥有大量的内置函数，编程也很简单，学生学习起来没有太大困难。在Wolfram Research 公司的网站上有专门的Wolfram Demonstrations Project 和 Wolfram Library Archive 栏目，其中有大量的量子力学（Quantum Mechanics）模拟实验或数学计算，以及相关的论文资料等，是很好的可利用资源。在教学中我们使用的是Mathematica 8.0的版本。

2 量子力学虚拟实验教学

我们的学生没有学过Mathematica，所以实验之前，教师先对程序中用到的主要函数、语句和语法规则进行讲解，然后让学生自己将教师预编好的程序录入计算机，并进行调试和运行。在程序能正确运行的情况下，按照实验要求修改部分参数，完成实验并记录试验结果。而对于Matlab 平台的实验，学生有一定的基础，我们会要求学生设计实验中的部分程序小段，然后调试和运行，修改实验参数，完成实验并记录实验结果。我校物理本科专业的《量子力学》开设64学时，其中我们安排了4个实验，每个实验2学时。下面我们挑选出2个实验进行介绍和讨论。

2.1 氢原子的电子云图（Matlab）根据量子力学的不确定性原理，电子在空间所处的位置和动量是不能同时被准确测定的，所以，在量子力学中，电子并无严格的轨道概念，而只能研究其位置的分布概率。因此，我们只能利用某个点附近电子分布的概率密度来描述电子的运动，并把这种概率分布形象地称为电子云。本实验的主旨就是用Matlab 来模拟不同电子数、不同电子能态的电子云图和氢原子核外电子的径向概率分布。

实验原理：氢原子最低的3 条能级的径向波函数为〔10〕:

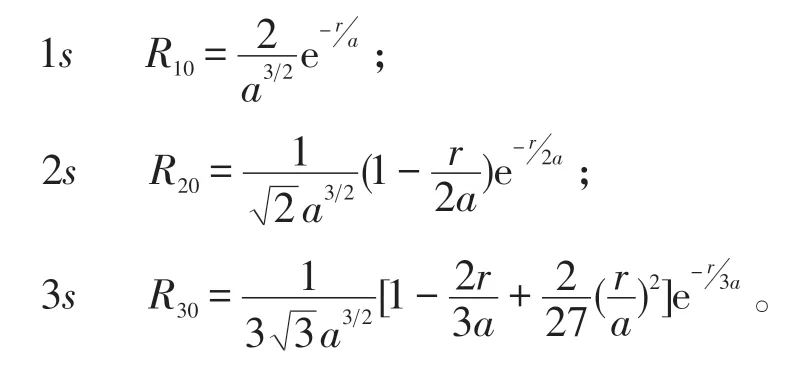
式中r为电子到原子核之间的距离，a为波尔半径。以上波函数都应满足归一化条件，而且概率密度是无量纲的，所以上面3 个波函数对应的概率密度可表示为〔11〕：

实验目的：①分别观察电子数为20 000和2 000情况下1s，2s，3s能态对应的电子云图和径向概率密度分布；②选择更少的电子数，观察3个能态电子云图的变化，直观感受波函数的统计特性。

实验步骤：①在Matlab 的编辑器中录入编制好的模拟实验程序，并在程序预留的“自行设计”区域，设计计算1s，2s，3s的径向概率密度的程序，并绘制概率分布曲线；②调试程序；③运行程序，并复制在电子数为20 000 和2 000 情况下3 个能态的电子云图和径向概率密度分布图；④自由选择电子数（少于2 000），观察实验结果；⑤完成实验报告。

实验结果：实验结果如图1～3 所示。由图1 和图3 可明显看出电子云图的差异，这充分显示了波函数的统计特性，对电子云图也有了更好的理解。

在实验的最后，我们要求同学选择更少的电子数（2 000 以下）来查看电子云图的分布，加深学生对波函数统计诠释的理解。

图1 电子数为20 000时的电子云图

图2 1s，2s，3s态的电子径向概率分布

图3 电子数为2 000时的电子云图

2.2 估测一维谐振子的能量本征值（Mathematica）粒子处在势场中的能量本征方程是量子力学的基本方程之一。求解能量本征方程的目的就是要找出能量本征值和能量本征函数。通常，一维谐振子的能量本征值是通过解Hermite 方程或者使用升降算符的代数解法得到的〔12-14〕。解Hermite 方程的过程很复杂，学生接受起来很吃力。代数解法虽然相对容易些，但我们教学中使用的是曾谨言编著的《量子力学教程》第二版，代数解法安排在第九章，而一维谐振子是第二章的内容〔15〕。为了帮助学生更好地理解能量本征方程的意义，我们在Mathematica 平台上为学生设计了一个用打靶法（shooting method）〔16〕解一维谐振子能量本征值的虚拟实验。

实验原理：一维谐振子的能量本征方程为

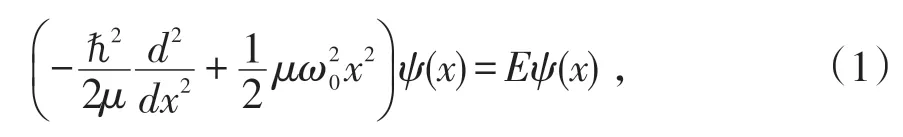
式中μ为经典谐振子的质量，w0是其自然频率。为了便于求数值解，我们将方程（1）标度化，可得

式中ε为标度方程（2）的本征值。

束缚态的波函数是有界的，所以解方程（2）的边界条件是ψ(±∞)→0 。按照shooting method 的思路，我们可以在ε=1，3等点的左右附近求出ψ～z的分布图，根据图形的变化情况以及曲线的交叉点数来确定ε=1，3是否是标度方程（2）的本征值。

实验目的：①熟悉利用NDSolve 函数求解标度方程的数值积分；②进一步熟悉Mathematica 的使用；③熟悉shooting method的解题方法。

实验步骤：①将教师编制好的程序录入计算机，并调试至正常运行；②估算基态的本征值：首先猜解ε=0.99，绘出ψ～z曲线，然后再猜解ε=1.01，绘出ψ～z曲线，观察曲线是否出现翻转。最后验证ε=1 是否就是标度方程的本征值；③求ε=3 的数值解并绘出ψ～z曲线，观察曲线是否有而且仅有一个交叉点（node）；④将ε=1、3的波函数归一化。

实验结果：如预期的一样，在ε=0.99和ε=1.01两个点的ψ～z曲线出现了翻转；ε=3 时，ψ～z曲线上有且仅有一个交叉点。结果如图4～9所示。

图4 ε=0.99

图5 ε=1.01

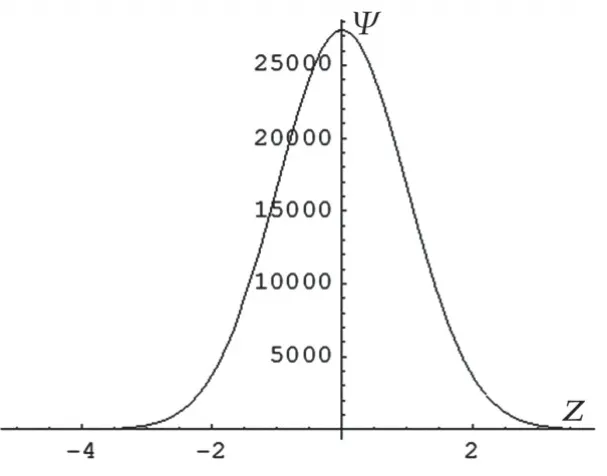
图6 ε=1.0

图7 ε=3.0

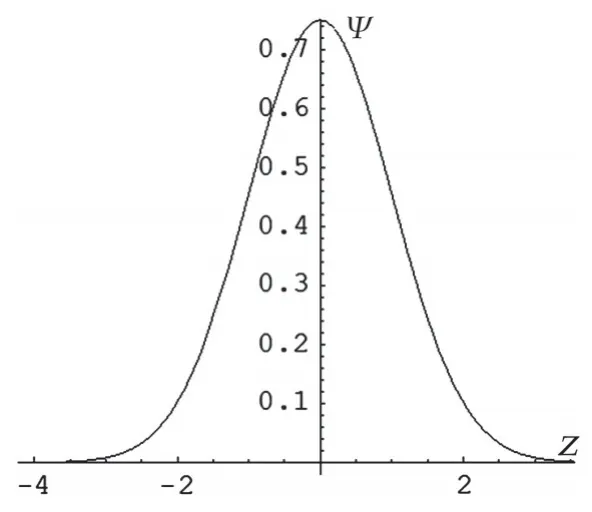
图8 ε=1.0归一化波函数

图9 ε=3.0归一化波函数

3 总结

在本校物理本科专业的量子力学教学中，我们进行了虚拟实验的教学尝试，共设计了电子双缝衍射、估测一维谐振子的能量本征值、隧道效应，以及氢原子的电子云图等4个实验。为了锻炼学生的动手能力，我们并没有使用Matlab 的GUI 模块对实验进行封装，而是采用完全开放的实验方式。教学中我们发现，学生对虚拟实验的热情很高。为了做好实验，不少学生还在网络上查阅相关的文献资料，在实验中也能提出一些平时不关心的专业问题。在期末考试我们发现，与虚拟实验相关的内容，学生的正答率很高。

量子力学是一门与经典物理学大相径庭、抽象、数学依赖性很强的课程，其教学一直是个难点。虚拟实验教学的引入，可以帮助调整学生学习的心理和学习态度，开阔学生的视野，对量子力学的教学起到了较好的促进作用。

〔1〕王祥高，秦松梅，顾运厅. 物理学专业量子力学教学探讨〔J〕. 广西大学学报:哲学社会科学版，2011，33（S）:253-254.

〔2〕单传家，陈入云，刘继兵，等.Mathematica 8.0.1中文版在量子力学教学中的应用〔J〕.湖北师范学院学报:自然科学版，2012，32（4）:92-96.

〔3〕王燕锋.多媒体课件在量子力学教学中的利与弊〔J〕.成宁学院学报，2010，30（12）:223-224.

〔4〕罗礼进，仲崇贵，方靖淮.量子力学WebQuest 教学模式的研究〔J〕.长春师范学院学报：自然科学版，2010，29（1）:99-103.

〔5〕陈高，孔梅，苟丽丹，等. 量子力学课程教学模式的探究〔J〕.吉林广播电视大学学报，2010（7）:54.

〔6〕杨希峰，刘玉申.激发学生学习的主观能动性:浅谈量子力学教学〔J〕. 常熟理工学院学报:教育科学，2010（6）:116-117.

〔7〕谢勇.物理类课程多媒体教学调查与分析〔J〕.红河学院学报，2012，10（3）:99-101.

〔8〕谢勇.西部普通高校量子力学双语教学研究〔J〕.保山学院学报，2012，31（2）:14-16.

〔9〕周建兴，岂兴明，矫津毅，等.MatLab 从入门到精通〔M〕.北京：人民邮电出版社，2008.

〔10〕曾谨言. 量子力学（卷I）〔M〕. 4 版.北京：科学出版社，2007.

〔11〕马涛.MatLab 版大学物理〔M〕.杭州：浙江工商大学出版社，2011.