用万能工具显微镜检测凸轮曲线的方法及测量不确定度评定

2014-03-22张日红胡玉明

计量技术 2014年1期

张日红　刘　芳　胡玉明　赵　楠　梁　静

(沈阳机床股份有限公司计量理化中心，沈阳 110142)

0　引言

凸轮是普通车床配套零件，作为主轴箱操纵机构的控制件，其曲线特征参数对于主轴变速起到重要作用。原有凸轮检查仪测量凸轮曲线时，在凸轮找正上花费了大量时间，工作效率低，为缩短检测时间，提高检测效率，本文介绍利用万能工具显微镜及其附件光学分度台实现凸轮曲线的快速检测，并进行了测量结果的测量不确定度评定，确保测量方法的可靠、有效。

图1　凸轮示意图

1　测量方法

图1为凸轮示意图，O点为凸轮基圆中心点。图2为检测用附具，附具的主要技术要求为圆度与同轴度，附具上部与凸轮基圆间隙配合，下部与光学分度台中心孔间隙配合，附具在测量过程中的作用是初始定位凸轮。附具的几何技术参数将凸轮基圆中心与光学分度台回转中心重合度控制在一定范围内，为找正凸轮提供测量条件。通过附具实现初始定位凸轮，简化测量定位过程，节约工作时间，提高工作效率。

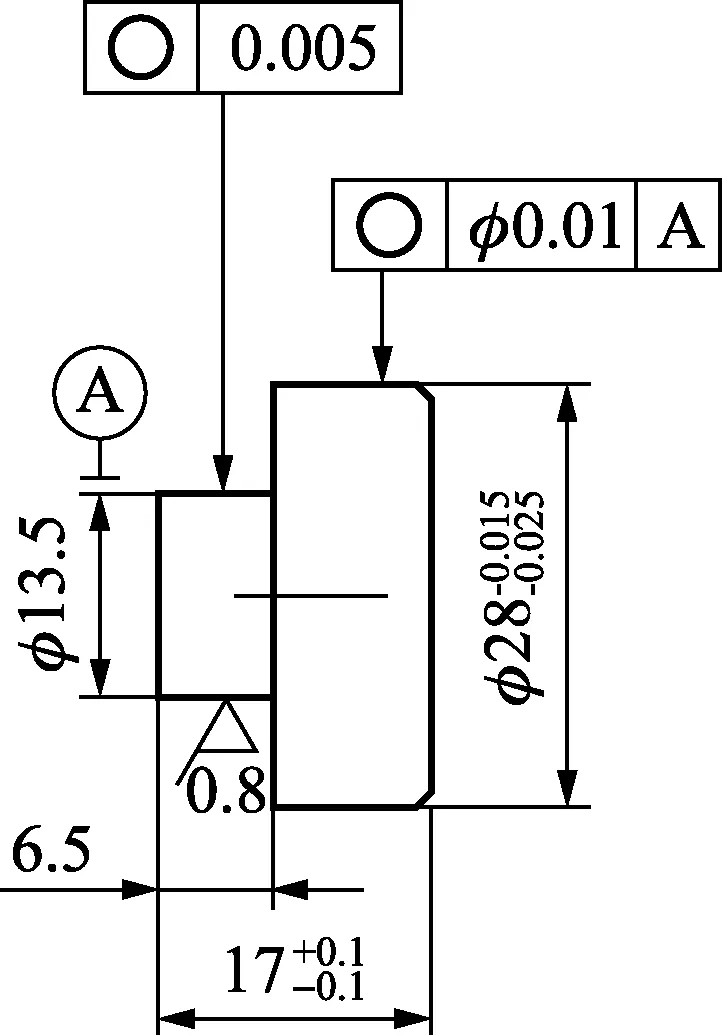
图2　测量用附具示意图

测量时，凸轮通过附具固定在光学分度台上，找正凸轮是使凸轮基圆中心与光学分度台回转中心相一致的过程。采用反光灯照射凸轮，万能工具显微镜米字线瞄准凸轮基圆边缘，转动光学分度台，使米字线与凸轮基圆边缘在360°内相切，即实现凸轮找正。找正凸轮基圆中心后，测量键槽轴线的基准角度值，再利用光学灵敏杠杆配备相应规格的测头与凸轮曲线特征点进行接触，配合光学分度台回转，实现凸轮曲线测量。

2　凸轮基圆中心横坐标定位误差分析

2.1　定位误差分析

定位误差由重复性引起，属于随机误差。在万能工具显微镜上，对凸轮基圆任意位置进行10次任意位置瞄准，横向坐标测得值为 35.977mm、35.972mm、35.967mm、35.967mm、35.973mm、35.979mm、35.974mm、35.975mm、35.973mm、35.977mm，计算其单次测量的实验标准差为

定位基圆中心横坐标时，其值由基圆上边缘坐标和下边缘坐标差的一半构成，则实验标准差为

式中：D为凸轮基圆横坐标。

ν=10-1=9

经过测量实验，估计D为正态分布，取p=99% 、νeff=9，查t分布表，得到t99(9)=3.25，则k99=3.25，计算其分布区间半宽为

a99=k99×s(D)=3.25×0.0032

=0.0104mm=10.4μm

则认为凸轮基圆中心横坐标定位误差范围为[-10.4μm,10.4μm]，其误差区间半宽度为10.4μm。

2.2　角度误差分析

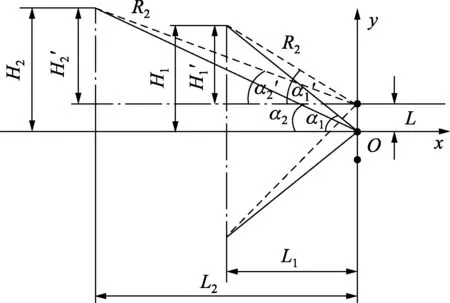
图3　凸轮键槽及特征点位置示意图

L变化范围[-10.4μm，+10.4μm]，得到几何关系如下：

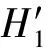
当L=0μm时，a1=arcsin(H1/R1)=12.3736°，H1=3mm，设键槽中心角度值为0°，则根据凸轮技术参数要求，得到a2= 10°，H2=8.1615mm，L1=13.6748mm，L2=46.2860mm。

同理，当L=-10.4μm时，中心角度示值变为0.0416°，测得凸轮特征中心点角度值为9.9709°，变化量为-105″。则凸轮基圆中心横坐标定位误差引起的角度误差范围为[-105″，105″]。

3　测量结果的不确定度分析与评定

利用万能工具微镜检测凸轮曲线的测量不确定度主要来源于光学分度台的示值误差、灵敏杠杆定位测量重复性、凸轮键槽中心角度定位误差和凸轮基圆中心横向坐标定位误差。由于不确定度与测量的凸轮曲线特征点位置有关，以 10° 为例进行分析与评定。

3.1　数学模型

a =(at-as)-Δa

(1)

式中：a 为凸轮曲线角度值，′；at为凸轮曲线特征点角度值，′；as为凸轮键槽中心角度值，′；Δa 为凸轮基圆中心点横坐标定位角度误差，′。

灵敏系数为

3.2　各影响量的标准不确定度来源分析与评定

3.2.1凸轮曲线特征点角度值at

凸轮曲线特征点角度值at引入的标准不确定度来源于光学分度台的示值误差和灵敏杠杆定位重复性，则

1)光学分度台的示值误差引入的标准不确定度分量u1(at)

根据 JJG 56—2000中对光学分度台示值误差的要求，最大允许误差为不大于30″，则其引入的标准不确定度为

2)灵敏杠杆定位重复性引入的标准不确定度u2(at)

利用灵敏杠杆瞄准凸轮曲线特征点进行10次重复定位，测得角度值为、89°19′、89°18′、89°19′、89°19′、89°19′、89°18′、89°19′、89°18′、89°19′、89°19′，计算其单次测量的实验标准差

标准不确定度为

u2(at)=29″

凸轮曲线特征点角度值at引入的标准不确定度u(at)为

u(at)=34″

3.2.2凸轮键槽中心角度值as

凸轮键槽中心角度值as引入的标准不确定度来源于光学分度台的示值误差和万工显目镜瞄准定位重复性，则

键槽中心角度值为两键槽边缘角度和的一半，进行不确定度评定时需进行合成。

1)光学分度台的示值误差引入的测量不确定度u1(as)

2)定位重复性引入的标准不确定度u2(as)

对凸轮一侧键槽任意位置进行10次重复瞄准，测得角度值为66°52′、66°51′、66°49′、66°49′、66°47′、66°48′、66°44′、66°45′、66°44′、66°43′，计算其单次测量的标准差为

标准不确定度为

凸轮键槽中心角度值as引入的标准不确定度u(as)为

u(as)=133″

3.2.3凸轮基圆中心点横坐标定位角度误差Δa

根据3.1及3.2分析，估计凸轮基圆中心横坐标定位角度误差在[-105″，105″]内等概率分布，标准不确定度为

3.3　合成标准不确定度的评定

凸轮曲线测量标准不确定度汇总表见表1。

表1不确定度汇总表

标准不确定分量u(ai)不确定度来源标准不确定度cici·u(xi)u(at)at引入的标准不确定度34″u1(at)光学分度台示值误差17″u2(at)灵敏杠杆定位重复性29″134″u(as)as引入的标准不确定度133″u1(as)光学分度台示值误差12″u2(as)瞄准定位重复性132″-1133″u(Δa)Δa引入的标准不确定度61″-161″

凸轮曲线测量合成标准不确定度为