螺纹单一中径的三针和量球法测量

2014-03-22刘远模

计量技术 2014年1期

关键词：中径跨线外螺纹

刘远模

(成都艾立特螺纹工具有限公司，成都 610512)

0　引言

本文从三针法测量外螺纹和量球法测量内螺纹时的空间笛卡尔坐标系，阿基米德螺旋面的参数方程出发，由测量接触点的单位法向量并用向量和关系求出该点曲线坐标和测量关系式导出检验计算和测试计算步骤，提供了用于数据验证的计算程序。

1　外螺纹的三针量法和内螺纹的量球测量法

外螺纹尤其是精密螺纹(如螺纹塞规)单一中径常用三针量法测量，如图1所示。测量时圆柱形状的量针轴线与螺纹轴线处于空间交叉位置，且量针与螺纹两牙侧曲面(轴向截型为直线的阿基米德螺旋面)分别接触于一点，求出其曲线坐标及相关的计算方法。

图1　用三针跨线测量外螺纹

图2　用量球测量内螺纹

内螺纹尤其是精密螺纹(如螺纹环规)单一中径可用量球法测量，如图2所示。测量时量球与螺纹两牙侧曲面分别接触于一点，求出其曲线坐标及相关的计算方法。

1.1　空间坐标系的建立

在螺纹的一侧槽中放置单根量针，在直径对面的两个对称槽中放置另两根相同直径的量针，用适当的测力测量这三根量针之间的跨线距离M，就可计算所述单根量针所在位置的螺纹单一中径。在图1中，建立笛卡尔空间坐标系Oxyz：沿螺纹轴线建立OZ轴，单个量针的轴线在OZ轴上的投影点O作为坐标系原点，两轴线为空间交叉直线，其距离为A，从点O沿垂直于量针轴线的方向建立OX轴，按右旋系统建立Y轴。显然，OX轴同时垂直于上述两轴线。OX轴与OZ轴的交点为O，与量针轴线的交点为O′，线段OO′=A(=m/2)。

沿OX轴并垂直于量针轴线的平面与量针的截形为直径ω的圆，在量针和螺纹都为刚体情况下，量针与螺纹的两螺旋面的接触点分别为点a和b，他们是量针的圆柱面与螺纹左右牙侧螺旋面的交点，每一个测量接触点都有一个公切面也就有一条公法线，根据静力学原理，这是交点的支承反力方向。显然，在XOZ平面中量针截形为椭圆，且不与螺纹截形接触，尽管螺纹截形为轴向截形。

在图2中，建立笛卡尔空间坐标系Oxyz：沿螺纹轴线建立OZ轴，量球球心为O＇，它在OZ轴上的投影点O作为坐标系原点，线段OO′=A(=m/2)，沿OO′方向建立OX轴，按右旋系统建立Y轴。

螺纹的左牙侧角为a1，右牙侧角为a2，导程为L，螺距为P，线数为n，显然L=nP。

在以后式中出现双号±或∓,上号用于外螺纹,下号用于内螺纹。

由△cde和△dgf分别得

(1)

(2)

1.2　曲线坐标的计算

右旋左右侧螺旋面表达式分别为

(3)

(4)

式中，l 为螺旋参数，l =L/(2p )，它是动点绕螺纹轴线转动单位弧度沿螺纹轴线所移动的距离。当l =0时，式(3)和(4)表示V型圆环槽的左右侧圆锥面表达式，这是螺纹曲面在l =0时的特例。

式(3)、(4)分别是左、右侧螺旋面上动点在高斯坐标系中的曲线坐标(r，θ)、(r1，θ1)与直角坐标之间关系式。对于坐标曲线r和θ，当r=常数时，坐标曲线θ为一条螺旋线；当θ=常数时，坐标曲线r为一条螺纹轴向截形直线。坐标曲线r1，θ1情况类似。

左右侧单位法向量N和N1[3]分别为

(5)

式中

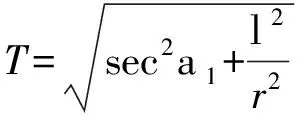
(5a)

(6)

式中

(6a)

上述两式中，i、j和k分别是笛卡尔坐标系X、Y和Z轴的单位向量。

1.2.1左侧曲线坐标的计算

由向量和Oa+aO′=OO′可得(xi+yj+zk)+0.5ωN=Ai，于是

(7)

(7a)

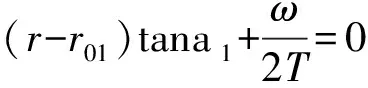
(7b)

由式(7a)得

(8)

显然，由式(8)可知θ为正，这对于外螺纹是毋庸置疑的，即使对于内螺纹也是对的，因为r>ω/2且T>tana1，所以分母也为正。由式(7b)可得

(9)

1.2.2右侧曲线坐标的计算

由向量和Ob+bO′=OO′可得(x1i+y1j+z1k)+0.5ωN1=Ai，于是

(9a)

(9b)

(9c)

由式(9b)可得

(10)

由式(10)可知，当分母为正时θ1为负，对于外螺纹分母当然为正，对于内螺纹因为r1>ω/2且T1>tana2，所以分母也为正。

式(9a)与(9b)联解，即sinθ1×(9a)-cosθ1×(9b)再代入式(9a)得

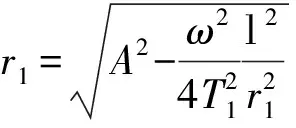
(11)

由式(9c)和式(1)分别得

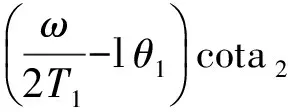
(11a)

r01=[r0(tana1+tana2)-

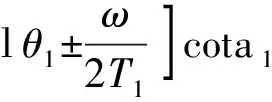
(11b)

1.3　运算

1.3.1迭代运算的初始化

令l =0，由式(8)和式(10)可知θ=0和θ1=0，这是V型圆环槽，于是由式(5a)、(6a)、(9)分别得

T=seca1，T1=seca2

r=r01±0.5ωcosa1cota1

(11c)

又由式(7)与(9a)联解得

r1=r±0.5ω(sina1-sina2)

(11d)

再由式(11a)、(11b)、(11d)和(7)可得

r02=r1∓0.5ωcosa2cota2

(11e)

(11f)

A=r±0.5ωsina1

(11g)

用量针对V型圆环槽的三针跨线测量见图3，用量球对V型圆环槽的测量见图4。用此两图不难证明上述式(11c)～(11g)是正确的。这也旁证了螺纹测量公式的正确性，因为V型圆环槽的三针跨线测量和量球测量分别是螺纹三针跨线测量和螺纹量球测量的特例。

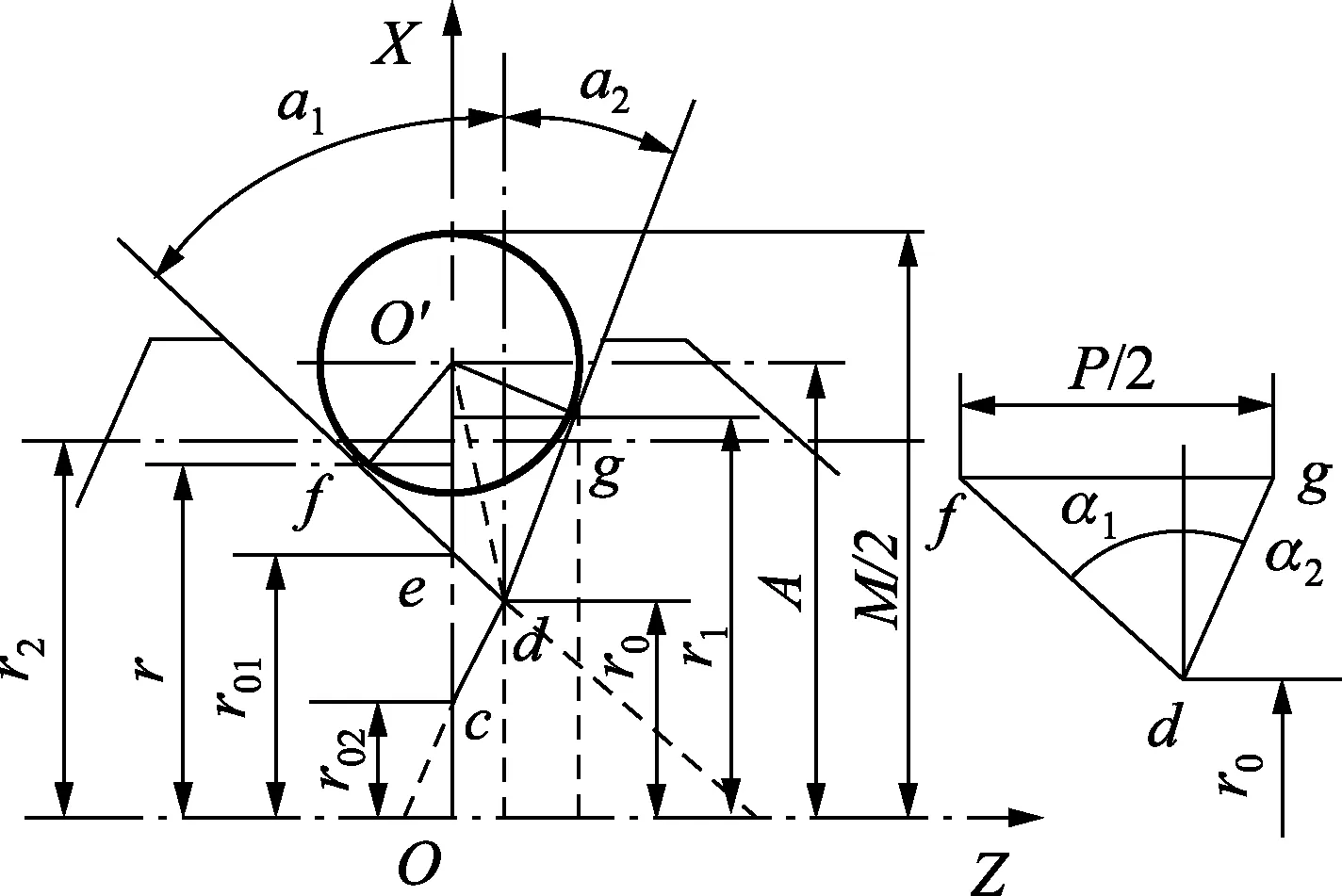
图3　V型圆环槽的三针跨线测量

图4　用量球测量V型圆环槽

三针跨线测量计算可分为两种：检验计算是根据中径d2求跨线测量值M或m；测试计算是根据跨线测量值M或m求实测中径d2。前者主要用于加工检验和成批验收检验，后者主要用于校准或标定检验。

1.3.2检验计算

已知螺纹类型、d2(D2)、a1、a2、n、P、ω按下述顺序计算：

1)初始值计算：式(2)计算r0→式(11f)、(11c)、(11d)和(11e)计算r01、r、r1和r02初始值。

2)迭代计算：以θ=0作为初始值代入式(9)然后与式(8)迭代→将达到某一准确度(例如1×10-7)的r和θ值代入式(7)计算A→代入式(11)迭代计算出r1，代入式(10)得θ1值→代入式(11b)计算r01→再按式(9)与(8)重复进行迭代计算直到r01达到某一准确度为止。

于是此时两测量接触点(图中a和b点)的曲线坐标分别为(r，θ)和(r1，θ1)。所获得的A值是满足两测量接触点的量针轴线与螺纹轴线之间距离或量球球心与螺纹轴线之间距离。

三针跨线测值或量球跨球测值M为

M=2A±ω

(12)

令l =0，将式(11c)、(11f)和式(2)代入式(11g)并令A0=A得

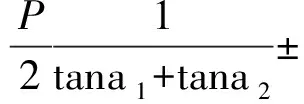
再代入式(12)得M0

(12a)

M0=d2±C

(12b)

式中：C为三针测量常数，按下式计算

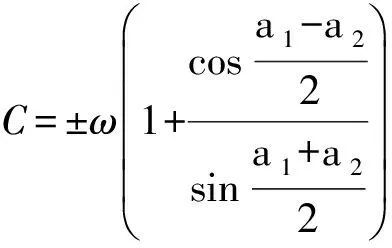
(12c)

显然

m=2A

(12d)

(12e)

斜置误差Δ为

Δ=M-M0=m-m0

(13)

M=M0+Δ=d2+C+Δ

(14)

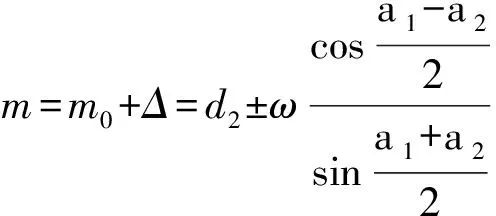
(14a)

d2=M-Δ-C

(15)

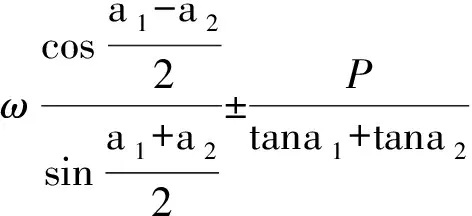
(15a)

检验计算由式(12a)和(12)分别求出跨线(球)测量值M0和M或(12e)和(12d)分别求出量球或跨线中心距m0和m，用式(13)获得斜置误差Δ，对于外螺纹Δ为正值，对于内螺纹Δ为负值，再由式(14)计算M或用式(14a)计算m，实际测量时对M或m的偏差就是中径d2的偏差。

1.3.3测试计算

测试计算由测得的M或m用下式计算A

A=(M∓ω)/2=m/2

(15b)

类似于式(11)的证明可得

(15c)

测试计算步骤：用式(11g)和(11d)分别求出初始值r和r1→用式(15c)迭代求解r，代入式(8)得θ→用式(7b)计算r01→用式(11)迭代求解r1，代入式(10)得θ1→由式(11a)计算r02→又用式(1)和(2)计算中径d2。斜置误差用式(12a)或(12e)和(13)计算。

1.4　讨论

1.4.1两种计算的关系

检验计算d2→M；测试计算M→ d2。正计算与反计算的已给值和所求值应该是可逆的，理论上应该相同，但由于四舍五入误差，在准确到小数后四位时，有0.0001mm的误差是可能的。

1.4.2Berndt公式结果差异原因

由图1或图2可知，量针或量球与两牙侧接触各有一个接触点，于是他们的曲线坐标分别为(r，θ)和(r1，θ1)，求出这些曲线坐标值就能为正确获得所需答案提供有效途径。但是Berndt公式[2]在计算锯齿螺纹时只有一个辅助角θ，因此这是其计算结果出现差异的原因。

1.4.3对称螺纹表达式

如果a1=a2=a /2，即对于对称螺纹代入上述各式就可得所求。对于V型圆环槽即l =0，由式(12c)、(12a)分别得

M0=d2±ω[1+1/sin(a /2)]∓0.5Pcot(a /2)

由式(11f)、(1)和(2)可得

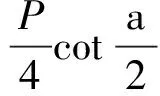
由式(11d)和(11c)得

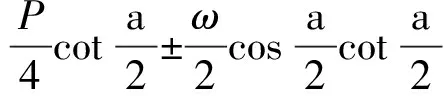
迭代时初始值用上述r1、r、θ=0和θ1=0，于是迭代后的结果r1=r，θ和θ1绝对值相等但符号相反。因此可一侧迭代计算获得结果。

跨线测量时，量针的跨线距离M与量针轴线距离m之间关系为

m=M-ω=2A；M=m+ω= 2A+ω

Berndt公式是用测值m计算实测中径d2。

2　程序简介

为了进一步理解前面的论述，有必要举出有代表性的计算实例说明。应用作者所编图5所示程序可以方便的得出数据，其中作者所述方法在此称为“准确” 方法，另外两种方法用人名称谓，Berndt和苏宗康公式将另文讨论。

图5

程序“螺纹单一中径的计算”

程序见图5。斜置误差Δ1按下述公式计算

Δ1=m-m0

(16)

=M-M0

(17)

=d20-d2

(18)

式(17)一般用于外螺纹跨线测量，也可用于内螺纹，式(16)内外螺纹测量都适用。对于外螺纹Δ1为正值，对于内螺纹为负值。测试计算可用式(18)计算，也可用式(16)计算。

测力所引起的压陷误差Δ2[1]，斜置测力综合误差Δ12按下式计算

Δ12=Δ1﹢Δ2

修正量k是误差Δ的反号值。修正量用于测试计算，误差用于检验计算。

程序中有4个框架：螺纹类型用于选择内或外螺纹；螺纹种类用于选择公制或英制螺纹，公制螺纹要求输入螺距，英制螺纹要求输入牙数/25.4，但其它长度尺寸单位仍为mm；计算类型选择测试计算或检验计算；计算方法三种方法之一，即“准确”、“Berndt”或“苏宗康”。下面的用于输入数字的文本框，当某一文本框输入后，按“Enter”键光标跳到下一个文本框中准备继续输入，当然也可用鼠标点击获得焦点。当光标跳到测力文本框后，如果只了解斜置误差情况，不必输入测力，对于外螺纹如果计算方法是“Berndt”或“苏宗康”之一，输入测力值也没用，输入值会变为0，对于内螺纹一般测力较小且是比较测量所以测力为0，焦点在测力文本框中(即光标在该框中闪耀)，按Enter键焦点进入“输入确认”命令按钮，按Enter键焦点进入“计算”按钮，再按Enter键于是在计算结果文本框中显示所需内容。