一种最速下降的贪婪迭代算法

叶坤涛，杨国珂，贺文熙

（江西理工大学理学院，江西赣州341000）

一种最速下降的贪婪迭代算法

叶坤涛，杨国珂，贺文熙

（江西理工大学理学院，江西赣州341000）

压缩传感应用于图像压缩重构的算法通常有凸优化算法和贪婪迭代算法两大类.一般而言，凸优化算法重构概率高、速度较慢，贪婪迭代算法具有较快的重构速度，但损失了重构质量.结合凸优化算法中的最速下降法及贪婪迭代算法中的正交匹配算法（OMP），提出了一种新的算法，并应用于一维信号和二维图像信号的压缩重构实验，且深入对比分析了不同降采样矩阵对新算法的影响.结果发现，对同一降采样矩阵，即使图像的纹理不同，新算法在重构质量及重构时间上都优于原始的OMP算法.

压缩传感；凸优化算法；贪婪迭代算法；最速下降法；正交匹配算法

0 引言

在图像压缩重构方面，人们都希望找到更好的压缩重构方法，使得图像的重构效果提高，即相同压缩比的情况下，重构图像的信噪比提高、重构速度加快.近年来，压缩传感理论在图像领域的应用研究逐渐深入，取得了较好的进展[1].

压缩传感理论应用于图像压缩重构的研究，是围绕三个方面来开展的，分别是信号稀疏基和稀疏方法的改进、降采样矩阵的改进、以及重构算法的改进.

对图像使用不同的稀疏基和稀疏方法，可以得到不同的重构效果.例如，2010年，岑翼刚等[2]提出

了基于单层小波变换的图像稀疏方法，对图像进行一层小波稀疏后，分别对三个高频进行压缩重构，再和低频部分结合重构图像，得到了更好的重构信噪比.2010年，练秋生等[3]按照图像可分成卡通部分和纹理部分，卡通部分又分为平滑成分和边缘结构的理论，对这三个部分，分别运用不同的稀疏基重构，得到更好的重构信噪比.2012年，尹晓慧等[4]对DCT层式压缩重构进行改进，即保留层式DCT变换的最高层系数，只对其余层高频子带系数进行压缩重构，提高了重构信噪比.

传统的降采样矩阵有随机高斯矩阵、局部傅里叶矩阵等，而选取不同的降采样矩阵，也将获得不同的重构速度和重构质量[5].例如：2013年，汪博峰等[6]根据图像进行小波变换后低频成分集中在左上角的特点，提出了一种优化降采样矩阵的方法，可以提高重构质量和重构速度.2013年，杨海蓉[7]提出了稀疏带状测量矩阵的概念，并按列对图像重构，解决了图像转换成一列时生成降采样矩阵较大的问题，在保证重构质量的情况下，计算速度大大提升.

压缩传感的重构算法，同样也对图像的重构效果有深刻影响.最速下降法、牛顿迭代法等凸优化算法，以及正交匹配追踪算法（OMP）、正则化正交匹配追踪算法（ROMP）等贪婪算法的应用，都对图像等信号的重构效果产生了不同影响.一般来说，凸优化算法的重构值更精确，耗时更长，而贪婪算法在损失一定的精确度的前提下使得重构速度相对较快，易于实现[8].

研究工作是围绕重构算法的改进来开展的.结合凸优化算法中的最速下降法和贪婪算法中的OMP算法的优点而得到了一种新的算法.对改进算法和原始OMP算法，在不同降采样矩阵的情况下，进行了深入的对比分析.仿真实验结果表明，在重构质量提高的同时，新算法还可以提高重构速度，且保留了贪婪算法易于实现的优点.

研究首先对算法的重构流程和思想给出详细论述，然后将其应用于一维信号及二维图像的压缩重构，且对重构效果进行分析，得到新算法具有更快的执行速度及得到更好的信噪比的结论.

1 最速下降的贪婪迭代算法

由压缩传感理论，已知测量值y，测量矩阵（降采样矩阵）为R，稀疏基为φ，可以通过求解式（1）来近似的重构出原信号的稀疏表示x，将φ乘以x就能得到重构的信号[9]:

实际中存在误差问题时，式（1）被转换为式（2）：

式（2）同样又可以转换为无约束的最优化问题式（3）：

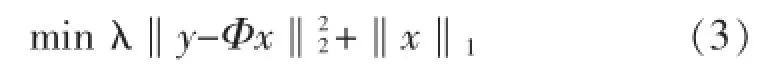
式（3）中，λ是一个正则化的参数，控制模型的收敛速度.

1.1 OMP算法

采用OMP的算法求解式（2）的流程如下[10].

输入：传感矩阵Φ，观测向量y，稀疏度K

输出：稀疏解x，残差r，迭代次数iter

初始化：r＝y，重构稀疏解x0，索引集合I＝Φ，迭代次数iter=0.

2）计算相关系数u=ΦTr，求出u中所得值的最大值，并将其对应的索引值存入索引集J中；

3）对J中索引值对应的原子存入集合I中，同时将Φ中该索引值对应的原子置0；

4）I=J∪I，得到支撑集ΦI；

5）利用最小二乘得到近似解x=（ΦTIΦI）-1ΦTIy；

6）更新迭代残差r=y-ΦIx，转步骤1.

1.2 最速下降法

若式（3）看成是一个多元函数f（x）的无约束优化问题，其寻优表达式可以用式（4）表示[11]：

其中，

每次的最优迭代步长tk通过求解式（6）获得.

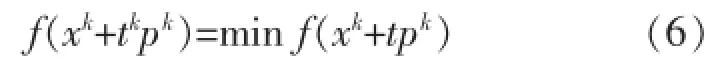
1.3 算法的改进

文献[12]指出，用以上最速下降法求解问题（3）时，本质上和OMP 算法一样，都是致力于使得每次迭代的重建误差‖y－Φx‖22最小. 且可证明迭代误差函数最小，可以等价为正定二次型函数的优化问题，即式（7）[12]:

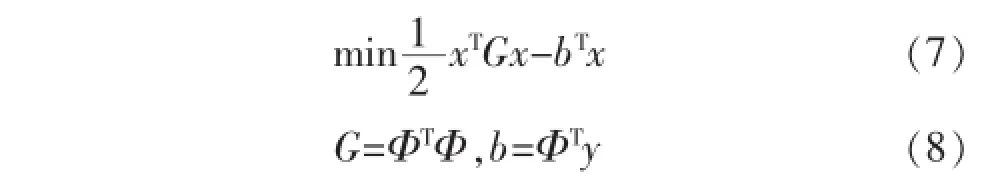
对式（7）求导得式（9）:

针对如上正定二次型函数，同样能够得到最速迭代步长tk的表达形式：

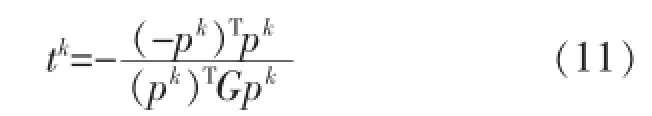
因为tk和pk都能用传感矩阵及残差表示，所以结合2.1节的OMP算法和2.2节的最速下降法，可以得到一新算法.新算法中使用式（4）对x进行更新，残差的更新公式为：

这样，新算法的流程为.

输入：传感矩阵Φ，观测向量y，稀疏度K

输出：稀疏解x，残差r，迭代次数iter

初始化：r=y，重构稀疏解x0，索引集合I=Ø，迭代次数iter=0；

2）计算相关系数u=ΦTr，求出u中所得值得最大值，并将其对应的索引值存入索引集J中；

3）对J中索引值对应的原子存入集合I中，同时将Φ中该索引值对应的原子置0；

4）I=J∪I，得到支撑集ΦI；

5）利用式（4）更新x，xk+1=xk+tkpk；

6）更新迭代残差rk+1=rk-ΦItkpk，转步骤1.

2 仿真结果

2.1 一维信号

对改进的算法进行了仿真测试.实验平台搭建在内存为2G的台式机上，使用的软件工具为Matlab2012.首先构造一个N=512，K=50的一维信号，降采样矩阵采用随机高斯矩阵.每个实验结果都是采用100次实验的平均值.实验结果如图1、图2、图3所示.

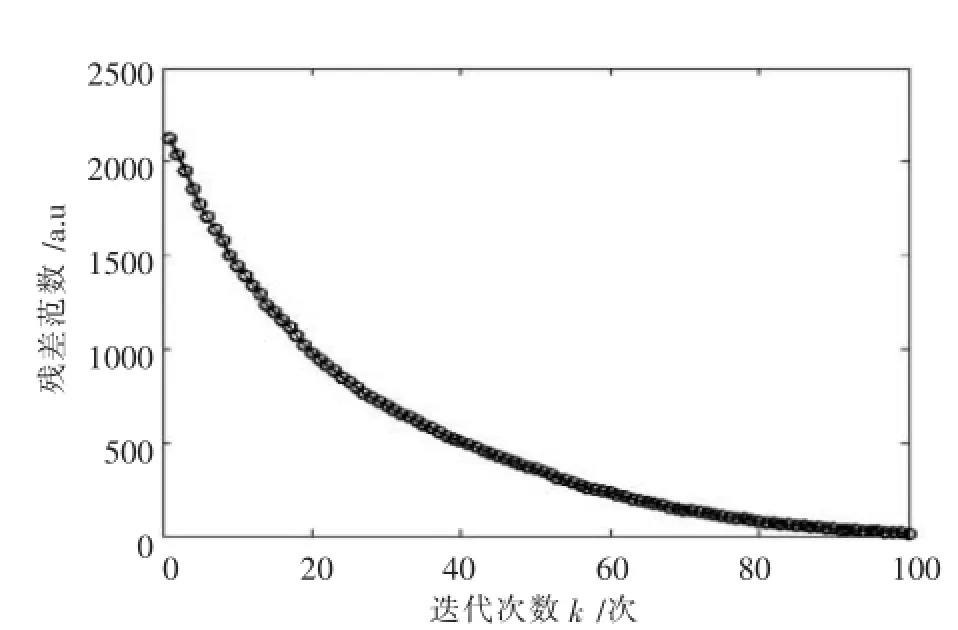
图1 残差随迭代次数变化

图1 反映的是残差范数‖rk‖2随迭代次数变化的关系图，残差范数随迭代次数增加，呈指数减小的趋势，即算法的收敛速度较快.随残差范数的减小，信号的重构质量提高，当残差范数减小到设定的阈值时，跳出算法的迭代，最后得到的结果即为重构信号.

图2为重构概率随采样个数的变化关系图.由图2可知，图像的重构概率随着采样个数的增加而增加，采样个数增加到120，重构概率达到100%，即原始信号可视为被精确重构.

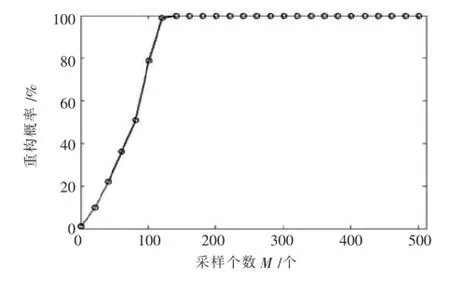
图2 信号重构概率随采样个数变化

图3 给出的是取采样个数为120时的重构信号与原始信号的对比图.可以看出，此时重构信号的包络与原始信号的包络完全重合，表示信号被精确重构.

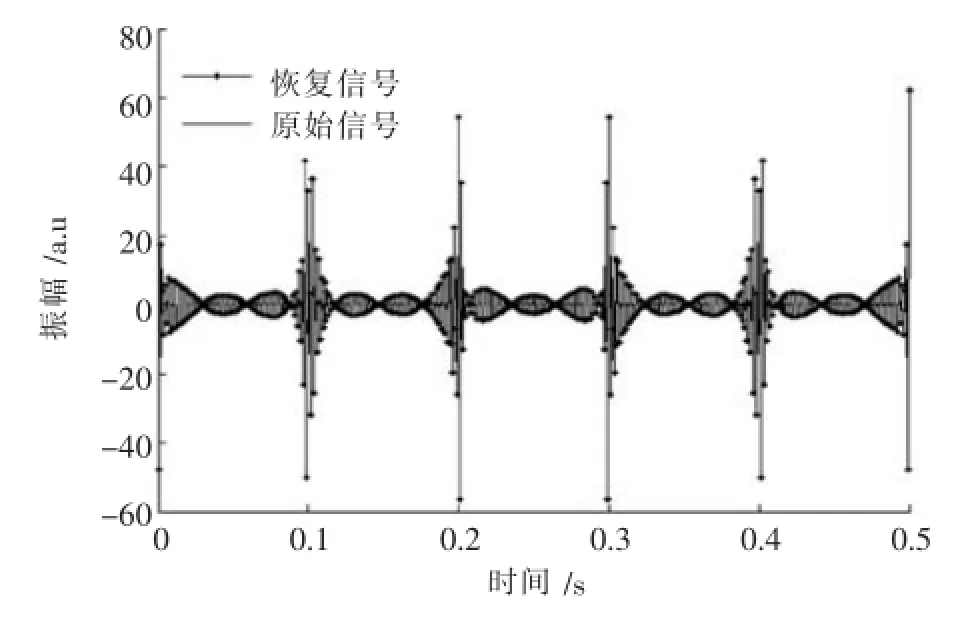
图3 原始信号与恢复信号对比

2.2 图像实验

同样的改进算法被应用于图像的压缩重构.图像实验中的稀疏基采用离散小波基，原始图像采用256×256的Lena图像，降采样矩阵分别采用高斯随机矩阵，置乱哈达玛矩阵及局部傅里叶矩阵，并进行对比分析.

将新算法与原始OMP算法从运行时间及信噪比两方面进行对比分析.重构图像的方法采用文献[7]按列重构思想.利用常用的峰值信噪比作为重构质量的评断标准，若x为原始图像，xˆ为重构图像，峰值信噪比的定义公式为：

在压缩比为0.5的情况下，实验结果如表1所示.表1中的实验结果均为算法运行100次的平均值.

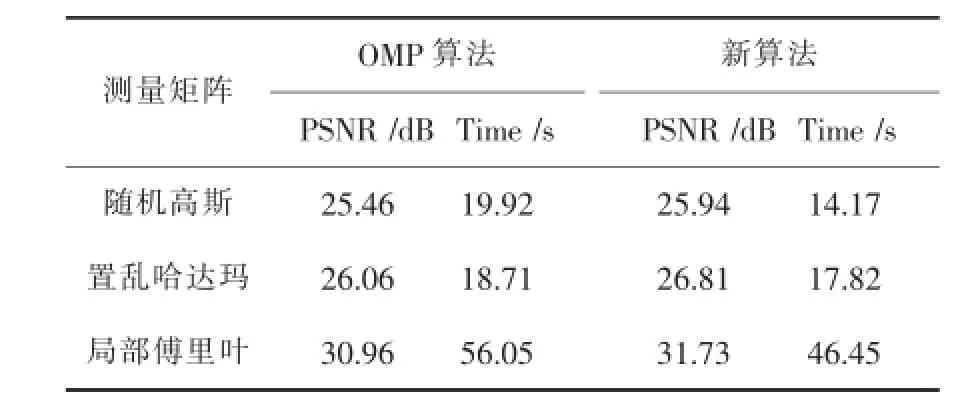
表1 各测量矩阵时的新算法与OMP的对比

由表1可知，在压缩比为0.5的情况下，降采样矩阵无论采用高斯随机矩阵、置乱哈达玛矩阵还是局部傅里叶矩阵，新算法不仅在信噪比上都优于OMP算法，而且重构时间也缩减.另外，表1还反映出采用不同的降采样矩阵，同一算法有不同的重构效果.

为了全面比较不同情况的重构效果，图4、图5、图6给出了在不同的压缩比时，降采样矩阵分别为随机高斯矩阵、置乱哈达玛矩阵和局部傅里叶矩阵时，新算法的重构质量、重构时间，与原OMP算法的比较.

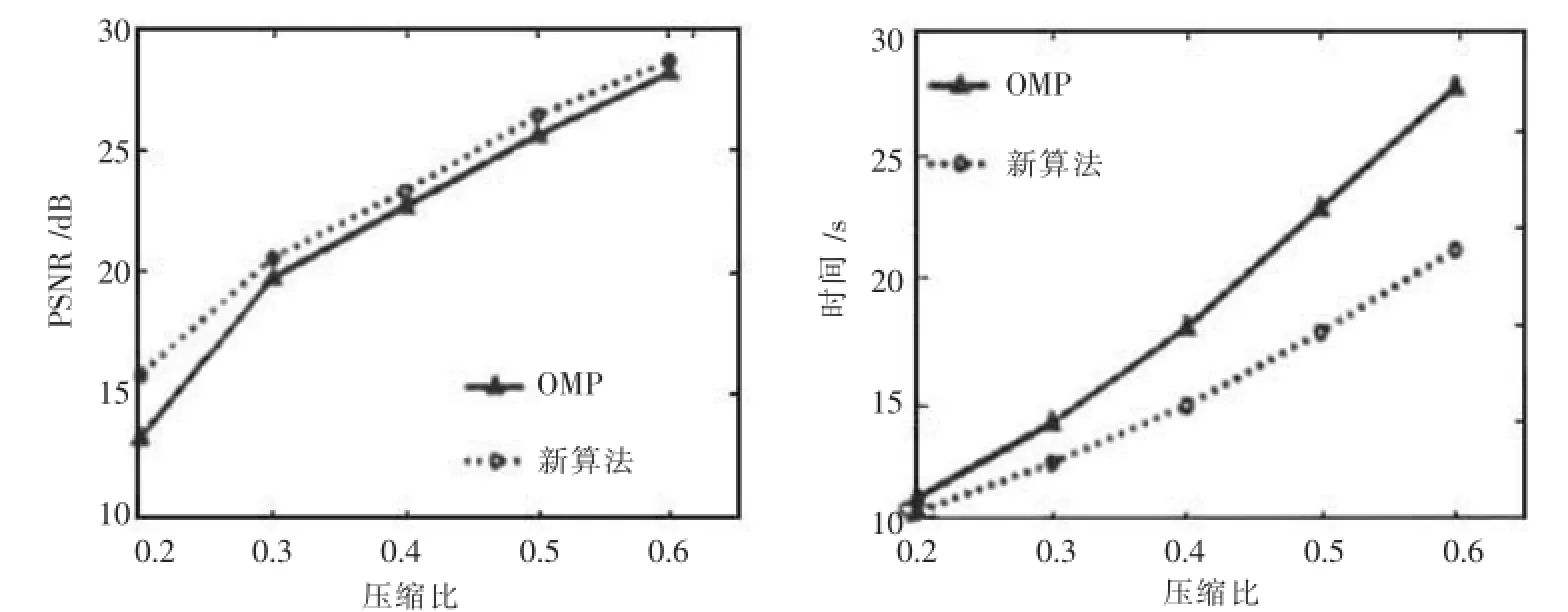
图4 随机高斯矩阵时重构信噪比和时间随压缩比变化

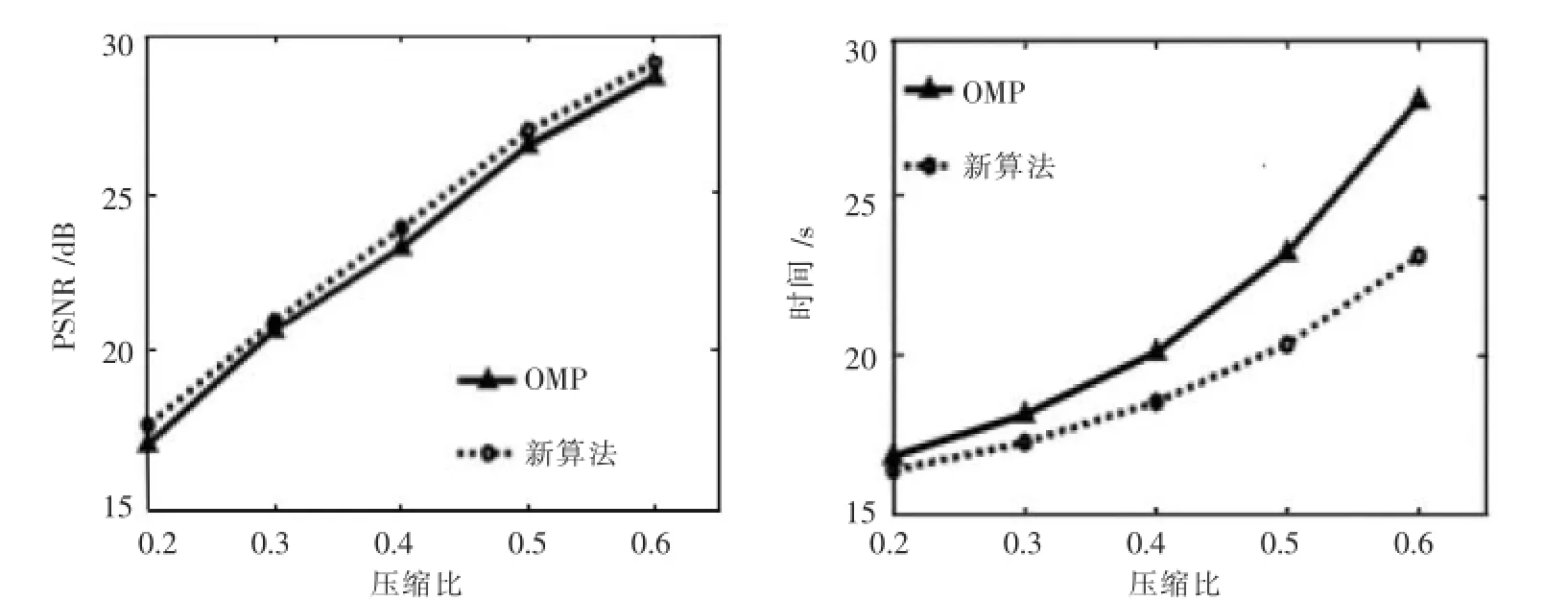
图5 置乱哈达玛矩阵时重构信噪比和时间随压缩比变化

图6 局部傅里叶矩阵时重构信噪比和时间随压缩比变化

从图4、图5、图6看出随压缩比增加，不同降采样矩阵下，新算法与OMP算法的重构时间都变

大，信噪比也都提高.特别是，对同一降采样矩阵，新提出的算法无论在重构信号的信噪比和重构时间上，都优于OMP算法.其中采用随机高斯矩阵与置乱哈达玛矩阵时，相比于局部傅里叶矩阵，具有较快的重构速度，但采用局部傅里叶矩阵可得到更好的重构质量.

为了验证新算法对不同纹理图像的重构效果都优于OMP算法，分别对Cameraman、Peppers、Boat这三幅纹理细节越来越复杂的256×256的图像进行压缩重构实验，重构效果如图7所示.

图7 三幅图像的重构效果对比（压缩比=0.5）

图7 中的重构实验，采用的压缩比为0.5，使用的降采样矩阵为局部傅里叶矩阵，图像所得重构时间T及信噪比P都是重构该图像所得的值.

显然，对于Cameraman图像，新算法重构的图像得到了更小的人眼可分辨的噪声区域.对于Boat图像，新算法重构的图像比OMP算法重构的

图像具有更少的模糊纹理.对于Peppers图像，虽然人眼很难区分出不同的重构效果，但PNSR与重构时间的数据仍表明新算法更优越.

3 总结

结合凸优化算法中的最速下降法及贪婪迭代算法中的OMP算法得出一种新的算法，通过实验分析得出针对不同的降采样矩阵和不同图像，新算法在重构效果及重构时间上都优于OMP算法.新算法的不足之处在于，虽然相比于OMP算法，信噪比有提高，但提高的幅度较小.类似的，结合正则化正交匹配算法（ROMP）与凸优化算法，还可以进一步的提高重构速度及质量.

[1]李树涛,魏丹.压缩传感综述[J].自动化学报,2009,35（11）: 1369-1376.

[2]岑翼刚,陈晓方,岑丽辉，等.基于单层小波变换的压缩感知图像处理[J].通信学报,2010,31（8）:51-55.

[3]练秋生,陈书贞.基于混合基稀疏图像表示的压缩传感图像重构[J].自动化学报,2010,36（3）:385-391.

[4]尹晓慧,张宝菊,王为，等.基于改进层式DCT的压缩感知图像处理[J].计算机工程,2012,38（9）:226-227.

[5]张成,杨海蓉,韦穗，等.基于随机间距稀疏Toeplitz测量矩阵的压缩传感[J].自动化学报,2012,38（8）:1362-1369.

[6]汪博峰,曹汉强.一种基于离散小波基的压缩传感测量矩阵优化方法[J].小型微型计算机系统,2013,34（9）:2193-2196.

[7]杨海蓉,方红,张成，等.基于稀疏带状矩阵的二维图像重构[J].计算机工程与应用,2013,49（10）:184-187.

[8]李珅,马彩文,李艳，等.压缩感知重构算法综述[J].红外激光工程,2013,42（1）:225-232.

[9]Donoho D L．Compressedsensing[J].IEEETransactionson Information Theory，2006,52（4）:1289-1306.

[10]Tropp J A，Gilbert A C.Signal recovery from random measurementsviaorthogonalmatchingpursuit[J].IEEE Transactions on Information Theory，2007,53（12）:4655-4666.

[11]龙建辉,胡锡炎,张磊.最速下降法解二次矩阵方程[J].湖南大学学报（自然科学版）,2008,38（4）:85-88.

[12]周灿梅．基于压缩感知的信号重构算法研究[D]．北京:北京交通大学,2010.

Greedy iterative algorithm of the steepest descent

YE Kuntao,YANG Guoke,HE Wenxi
(School of Science,Jiangxi University of Science and Technology,Ganzhou 341000,China)

When Compressed Sensing(CS)model is applied to the compression-reconstruction of the image, the solving algorithm usually can be categorized as convex optimization algorithm and greedy iterative algorithm.In general,the convex optimization algorithm has a higher reconstruction rate but a slower speed, while the greedy iterative algorithm has a faster speed with a loss of the reconstruction quality.Based on one of convex optimization algorithm,the Orthogonal Matching Algorithm(OMP),and one of greedy iterative algorithm,the steepest descent method,a new algorithm is proposed in this paper.And the new algorithm is applied to one dimensional signal and two-dimensional image signal for compression-reconstruction experiments.The different downsampling matrix effect of this algorithm is also analyzed.Results show that for the same downsampling matrix,the new algorithm is better than the original OMP algorithm both in terms of the reconstruction quality and the reconstruction time when applied for images with different textures.

compressed sensing;convex optimization algorithm;greedy iterative algorithm;the steepest descent method;orthogonal matching algorithm

TP391

A

2014-07-07

国家人社部2011年高层次留学人才回国资助项目（2011481）；江西省教育厅科技资助项目（GJJ11468）

叶坤涛（1972-），男，博士，副教授，主要从事MEMS、光谱测量与仪器等方面的研究，E-mail:kuntaoye@126.com.

2095-3046（2014）05-0073-06

10.13265/j.cnki.jxlgdxxb.2014.05.014