多级正向变异的遗传算法提高求解VRP问题效率
2014-03-22胡中栋谢金伟
胡中栋,谢金伟
(江西理工大学信息工程学院,江西赣州341000)
多级正向变异的遗传算法提高求解VRP问题效率
胡中栋,谢金伟
(江西理工大学信息工程学院,江西赣州341000)
应用遗传算法对车辆路径问题(VRP)求解时,由于遗传算法在解决VRP问题时,交叉操作难以保留优秀基因片段,可能导致算法收敛较慢等问题.在一定程度上影响了遗传算法解决VRP问题的实用性.在前人的基础上,通过一种多级正向变异方法,使变异最大程度向好的方向进行,拆除基因片段中较差的基因连接并建立新基因连接,从而得到较优的新基因片段,重复一定的变异次数,让变异达到最优效果.通过实验表明多级正向变异明显提高了遗传算法解决此类问题的效率.
车辆调度;遗传算法;多级正向变异;基因片段;算法设计
0 引言
车辆路径问题(VRP)是1959年由Dantzig和Ramser首次提出,它是指一定数量的客户,各自有不同数量的货物需求,配送中心向客户提供货物,由一个车队负责分送货物,组织适当的行车路线,目标是使得客户的需求得到满足,并能在一定的约束下,达到如路程最短、成本最小、耗费时间最少等目的[1].旅行商问题是VRP的特例,Gaery[2]已证明TSP问题是NP难题,所以VRP也属于NP难题,已经有多种方法来求解VRP问题[3-9],但启发式算法成为车辆运输问题求解的主要方法.遗传算法是其中一种方法,遗传算法是一类借鉴生物界的进化规律演化而来的随机化搜索方法.
应用遗传算法解决车辆路线问题(VRP)时,发现遗传算法进行交叉操作时易破坏原来较好的基因片段[10],从而导致算法效率降低.基于以上事实
提出多级正向变异的方法来提高效率.
1 车辆路径问题描述
设车辆的数量为M(m=1,2,…,M),单个车的容量为w.客户的个数为N,需求量为pi(i=1,2,…,N),且pi≤w.顶点集合为V={1,2,…,N}.用cij表示i点到j(j=1,2,…,N)的运输距离.xijm=1表示车辆m由客户i行驶到客户j,xijm=0表示车辆m没有经过这条路径.yim=1表示客户i的任务由车辆m来完成,yim=0则表示客户i的任务不由车辆m完成.
车辆调度的路径优化问题可建立数学模型[11]如下:
1)所有车辆以相同的起点同时向客户运输货物互不干扰.
2)车辆路径问题(VRP)的目标函数可定义为:
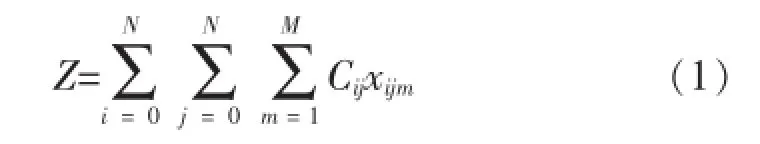
3)每一条路径上各个客户所需要的货物总重量不超过单辆车的载重量.
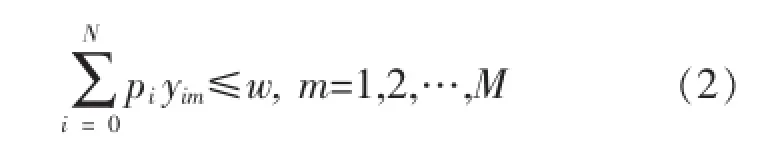
4)每个客户的需求只能让一辆车来完成,并且所有任务由K辆车完成.

5)每一个客户只能被一辆车服务一次.
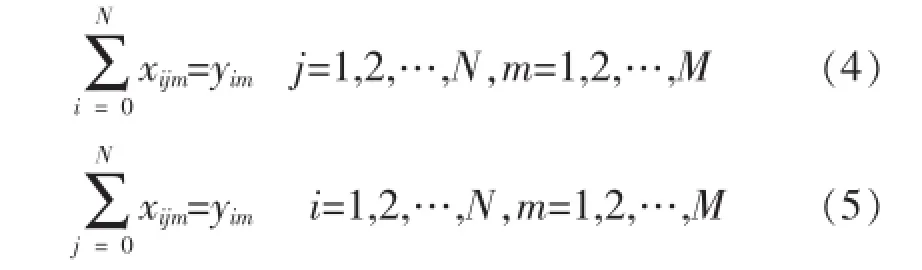
2 多级正向变异遗传算法基本思想与设计
2.1 基本思想
由于遗传算法解决VRP问题时存在编码问题,使得交叉操作可能无法保留优秀基因片段[10].针对因此而导致的算法效率较低的问题,经过算法分析与大量实验,提出利用多级正向变异的算法来提高解决VRP问题的效率.分析了传统遗传算法的变异过程,提出了改进为多级正向变异的方法.
1)自然界中的交叉操作是基因片段的重组,在解决VRP问题时的染色体交叉基因片段后,还需删除染色体中重复的基因.因此交叉操作有时可能会破坏原来相对较优的局部基因.从而造成遗传算法解决本问题时表现出不稳定并且收敛较慢的特点.
自然界中的变异是随机的,如果变异向坏的方向进行,就会产生更差的个体.差的个体将被淘汰,使问题达到最优解就要增加进化代数.在解决实际问题时,如果能通过某种简单的方法让变异尽可能向好的方向发展,那么进化的速度将加快,能够更快的收敛到全局最优解.
2)多级正向变异思想用以解决上述问题,具体问题是交叉操作导致优秀基因片段难以保留,而用多级正向变异的思想可以让变异尽可能多的向好的方向发展,减少进化代数,更快收敛到全局最优解.
多级正向变异的方法是在变异之前检查染色体中基因片段,如果该基因片段较差,则进行变异,随机生成新的基因片段;如果该基因片段较好,则不变异;对染色体重复合适的变异次数,使得变异的效果最好.变异产生更优染色体的概率大,且染色体的质量更高.这样,变异就最大可能性向好的方向发展了.
2.2 算法设计
应用遗传算法解决VRP问题时要进行编码、选择、交叉和变异等操作.
1)编码采用客户序号(序号是自然数1~L,L为客户数)的十进制编码方法.这种表示方法是直接产生L个1~L间的互不重复的自然数的排列,该客户排列就构成一个解,并对应一种配送路径方案.设客户排列(染色体)为41287635,设两辆车可以完成配送,每辆车为4个客户配送货物,则配送路线为第一辆车:0→4→1→2→8→0,第二辆车:0→7→6→3→5→0(其中0表示起始点)[12].
2)适应度计算方法采用某条染色体的配送方案中要经过的客户点(或起始点)之间的路径长度之和的倒数为其个体的适应值,设个体的适应值为f1=1/z(z为车辆所需行走路程的总和)[12].
3)选择操作采用轮盘赌的方式,首先计算种群中每个个体在该种群中的相对适应值随机生成一个[0,1]之间的数a,如果p1+…+pi-1 4)交叉采用顺序交叉法,开始选择一个匹配区域,设两父代个体及其匹配区域(设第3到第5基 因位,如A中的‘128’)为:A=34|128|765、B=52|847| 613;将两父代的匹配区域移动到对方的末尾得到A′=34|128|765847、B′=52|847|613128;去除原染色体中与A′和B′相同的数字得到新一代的染色体A′′=31265847、B′′=54763128. 5)传统变异方法与多级正向变异方法对比.传统变异为在同一个染色体内随机选取两个不同客户(基因)或多个客户进行交换或者插入到其他地方.例如将A=47856321的第二个客户“7”和最后一个客户“1”交换得到新的染色体B=41856327. 当Ci>Li时,则将i基因位处的客户移动到染色体末端,将i基因位标记为0,然后到i+2基因位处继续比较.当Ci≤Li时不进行任何操作,直接到i+1基因位处进行比较.重复以上操作直到染色体的最后一个客户,最后将标记为0的地方去掉,将客户(基因)顺序向前平移,得到新的染色体. 对每一条染色体重复上述过程一定的次数(通过实验确定次数),使得变异达到最优效果. 假设任一客户到其他客户之间的距离符合标准正态分布,单辆车来完成所有任务,f[i]表示i基因位的客户与i-1基因位处客户的连接.由标准正态分布的特点可知,Pm为标准正态分布的路径长度的期望,则随机两个客户间的距离有50%的概率大于Pm,有50%的概率小于Pm.若以Pm来作为标准,则如果连接长度比Pm大就认定为较差连接,比Pm小则认定为较优连接.可假设新形成的连接有50%是较优的,50%是较差的.本算法虽然会少量增加单代进化需要的时间,却能较大幅度减少收敛的代数和收敛时间. 以10客户点为例,图1~图4中圆圈表示客户点,带箭头的线表示线的起始点客户到终点客户之间的连接,五角星表示染色体连接中的较优连接,下方的数字表示染色体中的连接序号(即有向线段),假设原始染色体如图1所示. 图1 原始染色体 一级正向变异后如图2所示. 图2 一级正向变异后染色体 二级正向变异后如图3所示. 图3 二级级正向变异后染色体 三级正向变异后如图4所示. 图4 三级正向变异后染色体 综上所示,可以看到经过多级正向变异,10客户点的染色体已经很可能接近最优解.上述过程是单染色体特例,对一个群体来说这个过程会更长,一定级数正向变异后将不能继续优化染色体. 表1 各客户对货物的需求量/t 实验的环境:i5cpu笔记本电脑,8GB内存.在虚拟机(VMware)中安装2GB内存、单核cpu的ubuntu12.04系统.用C语言编写程序,数据分析与作图在R语言软件平台进行. 设Vi代表客户i,Qi表示Vi对货物的需求量,V0为起始点,则各客户对货物的需求量如表1所示. 各个客户间的距离如表2所示. 实验取客户数为10,初始随机产生数目为1000的种群,交叉长度为5,交叉概率为0.8,变异概率选择1(经实验确定),每辆车的最大载重量设为10 t,且车的数量不限.采用传统遗传算法与改进的多级正向变异遗传算法求解,在成功求解的概率都为98%以上的情况下,比较成功求解所用计 算的平均代数和平均所用时间(通过预先设定合理固定进化代数,传统变异设为1000,多级正向变异设为100,算法自动记录每一次成功求解所需代数和时间来实现).实验的数据均为运行程序1000次的平均结果.从图5与图6可知改进的多级正向变异遗传算法优势较明显. 表2 各个客户间的距离/km 图5 变异级数成功求解所需代数关系图 图6 变异级数成功求解所需时间关系图 设变异级数为K(K为0代表传统变异),传统变异平均成功求解代数为OG,平均成功求解时间为OT.多级正向变异平均成功求解代数为NG.平均成功求解时间为NT.表3为不同变异级数和平均得到最优结果所用计算代数的关系,表4为变异级数与平均得到最优结果所用时间关系.由于表格宽度的限制,在表1与表2中省略了P=2、4、6、8、10时的计算结果.图5、图6中的小圆圈连接的曲线表示传统变异的遗传算法运算结果,三角形连接的曲线表示本文设计的正向变异遗传算法的运算结果. 可以看到当变异级数为0时,即采用传统的变异方法求解时,收敛速度非常慢,成功求解所需的代数和时间都比较大.而采用本文设计的多级正向变异算法时,算法效率有较大幅度的提高,原因就在于设计的算法充分的利用了数据内部的联系,使得遗传算法向较合理的方向进行进化.通过实验表明,当采用多级正向变异算法时,仅在1级的情况下,提高的幅度已经非常明显,在8级变异时,算法的效率最高,找到最优解仅需要0.022 s,而传统变异方法则需要0.21 s左右. 表3 变异级数成功求解所需代数关系 表4 变异级数成功求解所需时间关系 经过10客户数不同正向变异级数情况下问题求解效率的分析,可以确定多级正向变异的方法对VRP问题的改进效果是非常明显的.多级正向变异方法可以最大程度的减少随机变异产生的较差结果所多耗费的时间和资源,从而提高遗传算法求解VRP问题的效率. [1]Paolo Toth,Daniele Vigo.The vehicle routing problem[M].Beijing: Tsinghua university Press,2011.[2]祝崇俊,刘民,吴澄.供应链中车辆路径问题的研究进展及前景[J].计算机集成制造系统,2001,7(11):1-6. [3]Christofides N,Mingozzi A,Toth P.Exact algorithms for the vehicle routing problem,based on spanning tree and shortest path relaxations[J].Mathematical Programming,1981,20(1):255-282. [4]Achuthan N,Caccetta L,Hill S.An improved branch-and-cut algorithmforthecapacitatedvehicleroutingproblem[J]. Transportation Science,2003,37(2):153-169. [5]张丽萍,柴跃廷,曹瑞.有时间窗车辆路径问题的改进遗传算法[J].计算机集成制造系统,2002,8(6):451-454. [6]宋厚冰,蔡远利.带时间窗的车辆路径混合遗传算法[J].交通运输工程学报,2003,3(4):112-115. [7]Ball M O,Golden B L,Assad A A,et a1.Planning for truck fleet size in the presence of a common carrier operation[J].Decision Sciences,1983,14(1):103-120. [8]赵燕伟,吴斌,蒋丽,等.车辆路径问题的双种群遗传算法求解方法[J].计算机集成制造系统,2004,10(3):303-306. [9]肖健梅,李军军,王锡淮.求解车辆路径问题的改进微粒群优化算法[J].计算机集成制造系统,2005,11(4):577-581. [10]邬开俊,王铁君.基于改进差分进化的车辆路径优化算法[J].计算机工程与应用,2013,49(13):17-20. [11]张瑞锋,汪同三.新型遗传算法求解车辆路径问题研究[J].湖北大学学报(自然科学版),2012,34(2):239-242. [12]郎茂祥.物流配送车辆调度问题的模型和算法研究[D].北京:北方交通大学,2002. [13]王晓博,李一军.多车型单配送中心混合装卸车辆路径问题研究[J].系统工程学报,2010,25(5):629-636. Multi-level forward mutation genetic algorithm to improve the efficiency for VRP HU Zhongdong,XIE Jinwei When using genetic algorithm to solve VRP problem,a slower convergence problem may be generated because the crossover operation could not keep good genes,which affects the usefulness of genetic algorithms to solve the VRP problem to a certain extent.On the basis of our predecessors,we have created a multi-level forward mutation method which dismantles poor gene fragment connection and creates a new connection to get a better gene.A large number of experiments show that forward mutation can greatly improve the genetic algorithm to solve such problems efficiently. vehicle scheduling;genetic algorithm;multi-level forward mutation;gene fragment;algorithm design TP301.6 A 2014-07-15 胡中栋(1958-),男,教授,主要从事智能计算和无线传感器网络等方面的研究,E-mail:jxhzd@163.com. 2095-3046(2014)05-0069-04 10.13265/j.cnki.jxlgdxxb.2014.05.013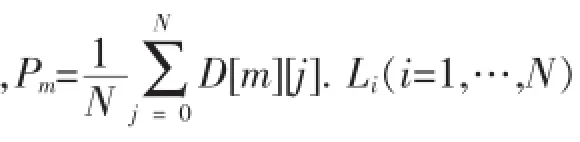





3 仿真实验


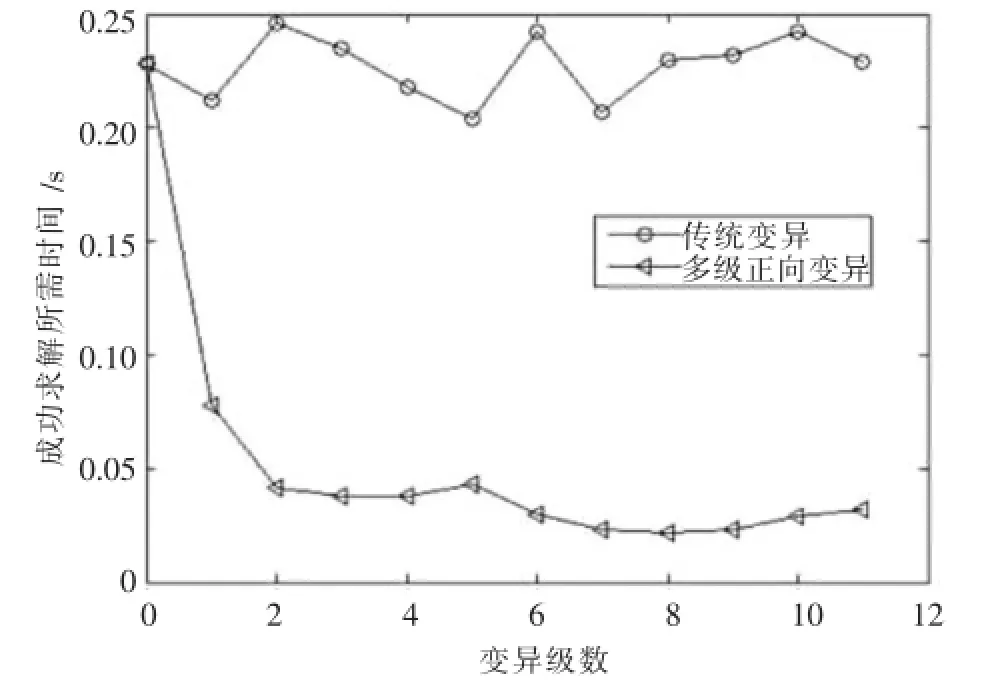
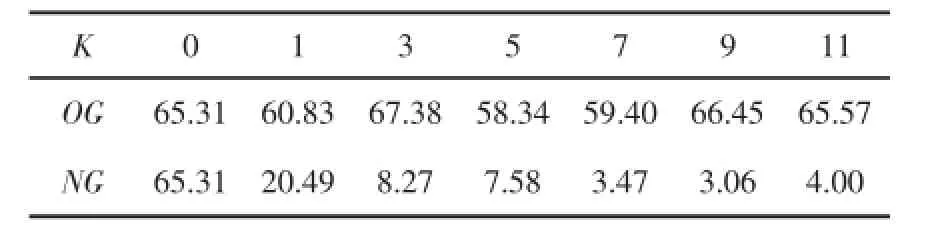
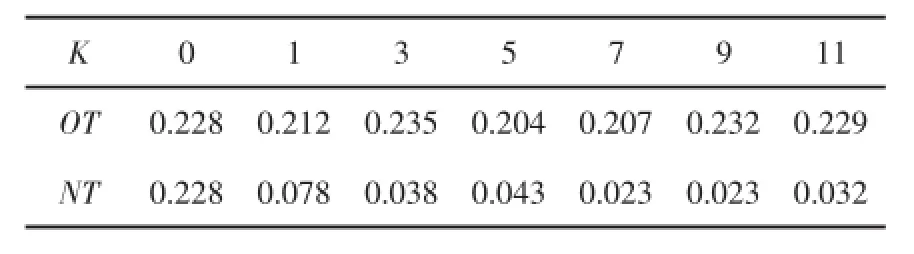
4 总结
(School of Information Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China)
