噪声声谱控制算法的研究

王萌 王晓晖 贺智国 张静

噪声声谱控制算法的研究

王萌 王晓晖 贺智国 张静

（北京强度环境研究所，北京 100076）

噪声声谱控制是噪声环境试验的重要环节，其控制是指控制倍频程或1/3倍频程频带的声压级。针对当前声压级谱控制中低频部分控制精度不够，实时性较差等问题，提出了一种新型的声谱控制方法。按照GB/T 3241-2010中的要求设计1/3倍频程滤波器，并根据声压级谱频段划分的特点和抽样率变换理论，提出了适合实时系统实现的滤波器复用方法和控制算法架构。

声谱控制；信号处理；1/3倍频程滤波器；抽样率变换

0 引言

噪声环境试验是为了确定飞行器所产生的噪声场对设备的影响而进行的试验。良好的噪声试验应当造成这样一个声场：它能使飞行器结构在地面上复现飞行中的振动场和内部声场，其结构在一定程度上就如同进行了飞行试验一样。因此，进行噪声环境试验，主要目的是为了验证飞行器设备能承受规定的噪声环境，而不出现不可接受的功能特性、结构完整性的衰退。目前，噪声环境试验已经成为飞行器研制过程中或投入使用前的一项重要的常规试验类型[1]。

目前噪声环境试验的声谱控制算法主要是通过控制驱动信号的功率谱密度（PSD方法）而实现的，与一般的随机振动谱控制在原理上基本相同[2][3]。声谱分析时首先需要得到信号的功率谱密度函数，由于其频率间隔为常量，在低频段控制的谱线数少，高频段控制谱线数多，造成低频控制精度低。为了实时有效地控制每个1/3倍频程，本文对噪声试验的声压级谱频段特点进行了研究，在此基础上提出了专门针对1/3倍频程频带控制的方法。利用滤波器采集得到包含每个1/3倍频程频带成分的信号，并进行实时处理分析，最终得到驱动信号。本文使用Matlab软件对6个倍频程（中心频率从31.5Hz到1000Hz）进行了算法设计仿真，实现了对噪声声谱的控制。

1 噪声声谱控制方法

1.1 声谱控制的PSD方法

该方法是目前控制器使用的常规控制方法，利用逆Welch方法生成驱动信号。将采集得到的信号通过计算功率谱密度来得到声压级，通过比较声压级的差值修正功率谱密度，从而修正驱动信号，完成对声谱的控制[4]，如图1所示，其中C为修正系数。在进行声谱分析时，如图2所示，将采集得到的时间历程信号，通过计算得到其功率谱密度，然后加窗得到不同1/3倍频程信号的均方根值，进而计算出不同频带的声压级；在进行驱动信号修正时，一般直接对驱动的功率谱进行比例修正。

图1 PSD方法的控制流程

图2 PSD方法的声谱分析过程

1.2 声谱控制的滤波器方法

为了实时有效地控制每个1/3倍频程频带，本文对噪声试验的声压级谱频带特点进行了研究，在此基础上提出了针对1/3倍频程频带控制的方法,即利用滤波器采集得到包含每个1/3倍频程频带成分的信号，并进行实时处理分析，最终得到驱动信号。贺旭东等人[13]提出了使用滤波器生成随机振动试验驱动信号的方法，验证了该方法在驱动信号生成中的可行性。数字滤波器一个重要性质是其频带可归一化（范围从0-1），在不同的采样率设置下，其截止频率也随之变化[14]。利用此性质和声谱的倍频程描述方式，只需要设计3个1/3倍频程滤波器（增益可变），通过下采样改变采样率的方式，便可以完成所有倍频程（中心频率从31.5Hz到8000Hz）共27个1/3倍频程的频带分析和幅值调整。当然，此处除了3个1/3倍频程滤波器外，还有用于上采样和下采样的低通滤波器，所以在理想情况下，使用4个数字滤波器可实现所有频带的声谱分析与控制。综上所示，本文以控制6个倍频程为例（中心频率为31.5Hz～1000Hz）设计了分频段控制的数字滤波器，利用滤波器增益来调整驱动信号的新型算法。

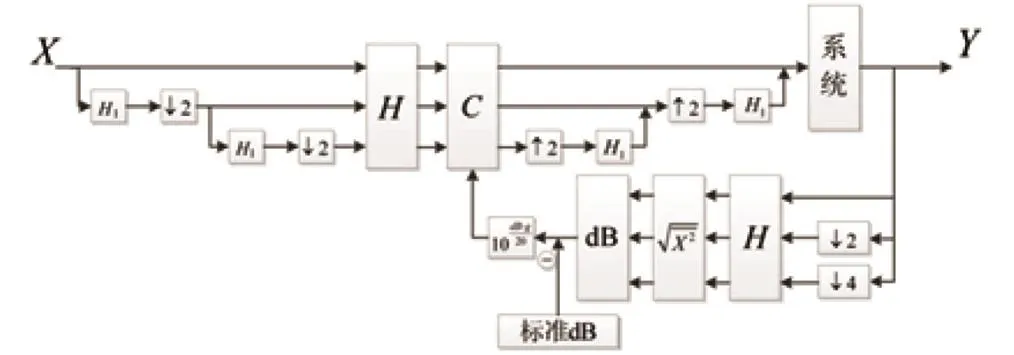
图4 滤波器方法控制流程

如图4所示，X为白噪声序列；Y为驱动；H为带通数字滤波器（由3个1/3倍频程滤波器组成），可对一个倍频程内的3个1/3倍频程分别进行增益可调的带通滤波；

设计中使用了8个滤波器，升采样和降采样过程各使用一个低通滤波器（滤波器参数相同），采集和驱动生成过程各使用3个1/3倍频程带通滤波器。

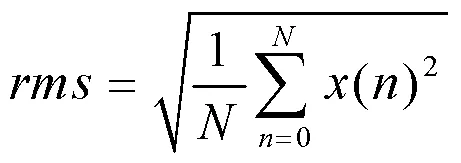
图5 信号采集分析

如图5所示，时间历程信号序列每个点通过滤波器后都会进行平方和计算，直到积累到一定数据量后再进行最后一步的平均求根计算得到均方根值，从而计算出声谱，该过程运算的实时性较强。

2）驱动信号生成：若对每个1/3倍频程设计一个滤波器，6个倍频程需要18个滤波器，并且在同一个采样频率下设计所有滤波器，无法设计低频段的滤波器。如图6所示，解决方法是针对最高中心频率为1000Hz的倍频程带宽设计3个1/3倍频程滤波器（一组），信号通过滤波器后得到该中心频率的倍频程带宽的信号；对原始信号进行降2倍采样率处理后，再通过上述同一滤波器组（滤波器增益不同），就得到中心频率为500Hz的倍频程带宽的信号；经过多次上述降采样处理就可以分别精确地得到中心频率为250Hz、125Hz、63Hz和31.5Hz倍频程带宽信号。最后对所有降采样的信号进行升采样处理，在同一个采样频率下将所有倍频程信号叠加就得到了全频段的信号，即驱动信号。在降采样和升采样过程中，不同倍频程的信号延迟不同，需要保证相位一致才能得到重构信号。

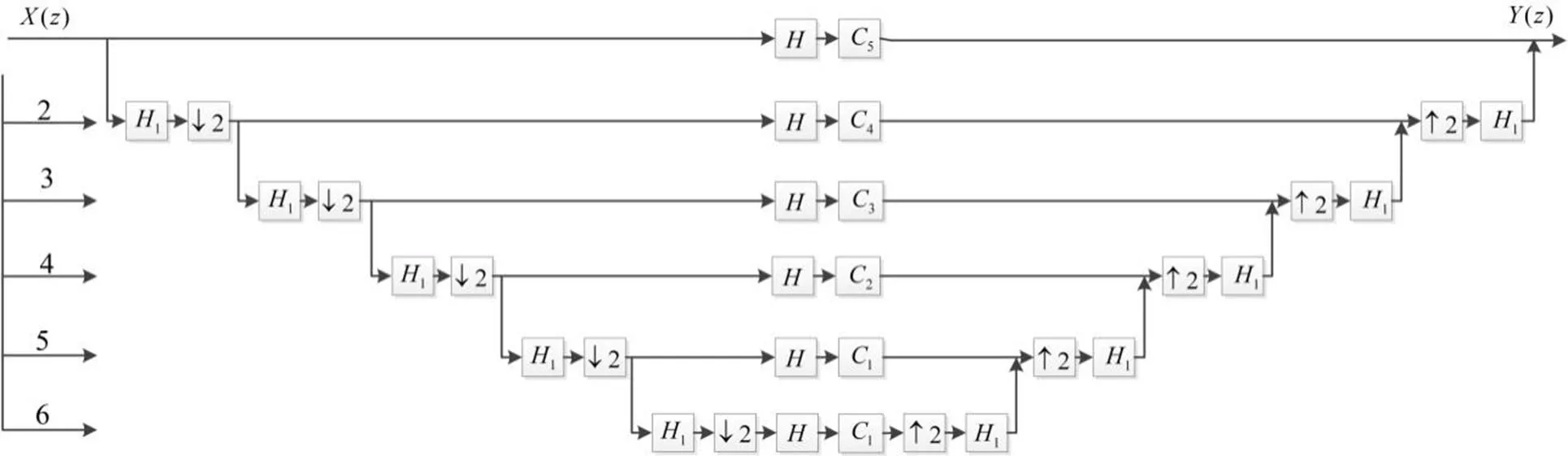
图6 信号生成过程

3）闭环控制：如图7所示，根据响应声压级与参考声压级的差异，通过修正滤波器增益来修改驱动信号。修正的原理是将采集得到的信号，经过不断地低通滤波和降采样，然后通过1/3倍频程滤波器组，得到每个1/3倍频程带宽的分信号。这些分信号互不影响，根据这些信号求得其声压级，然后在每个1/3倍频程带宽上比较响应声压级谱和参考声压级谱的差异，求得每个1/3倍频程上的声压级差值，根据差值修正滤波器增益，然后为下一次闭环控制产生新的驱动信号。首先选择随机信号作为初始驱动，然后以它为修正对象进行循环迭代，直到得到的响应声压级谱近似参考声压级谱。因为每个倍频程的信号采样频率不同，低频和高频部分都能够精确的进行控制修正。

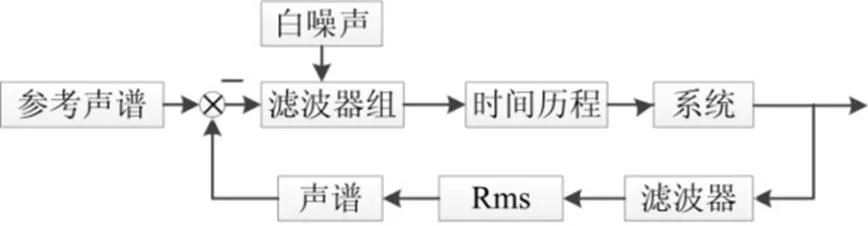
图7 信号闭环控制

2 滤波器设计

在驱动信号生成和数据采集过程中，信号需不断的通过滤波器处理，为了得到有效地控制信号，对滤波器的设计提出了要求：1）相邻两个1/3倍频程滤波器过渡带不能有很大的影响；2）不同路数据通过滤波器后相位延迟不同，叠加后需保持线性相位；3）滤波器阶次不宜过高，避免增大计算难度。

2.1 1/3倍频程滤波器设计

2.2 滤波器的选择

根据数字滤波器的冲激响应特性，可以将数字滤波器分为有限冲激响应滤波器（FIR）和无限冲激响应滤波器（IIR）[14]。

无限冲激响应IIR可用下面差分方程来描述

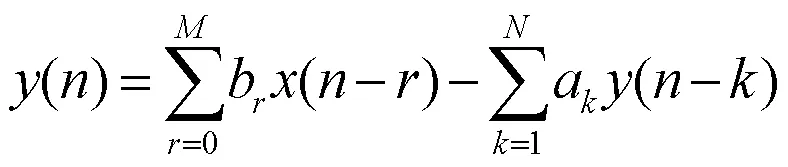
对应的系统函数为

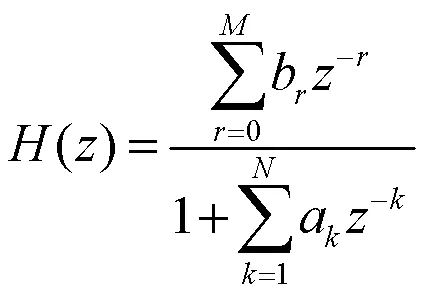
有限冲激响应FIR的差分方程描述为

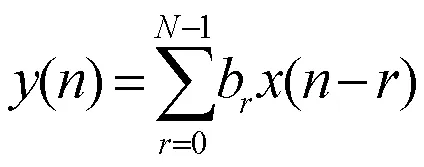
对应的系统函数为

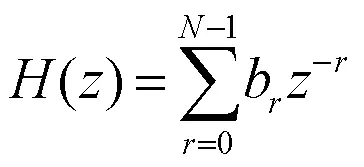
噪声控制器对数字信号处理的实时性要求很高，因此设计滤波器时考虑滤波器计算量的大小。IIR滤波器实现简单，其通带平坦，但不具备线性相位的功能；相对而言，FIR滤波器在同等滤波性能下，阶次虽远远高于IIR滤波器，但最大优点是线性相位，对于波形的分解和合成均有极大的好处。在控制算法中，时间历程在经过滤波器和上下采样后，还需要进行算术叠加，这要求各分信号的相位特性要完全一致。若滤波器均为FIR滤波器，经过适当设计和调整，FIR的线性相位特性可使得各个时间历程的延迟一致，最终叠加后的时间历程拥有很好的谱形，如图8所示。

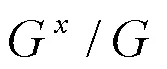
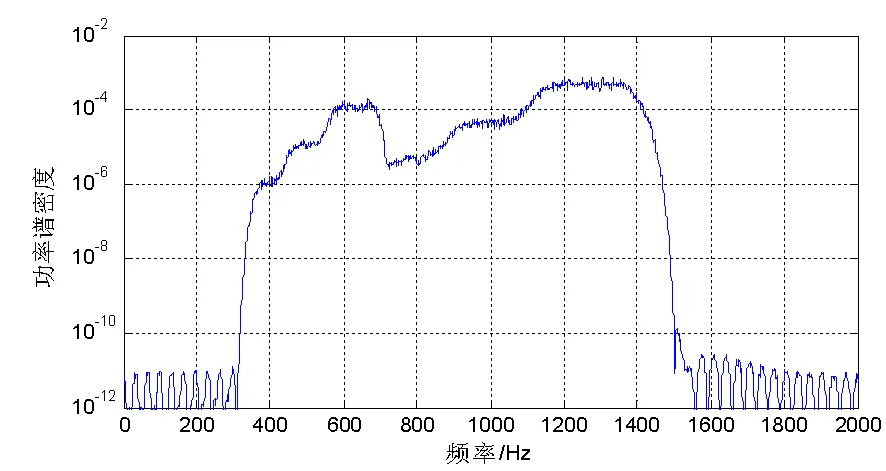
图8 两路信号延迟一致前后叠加效果

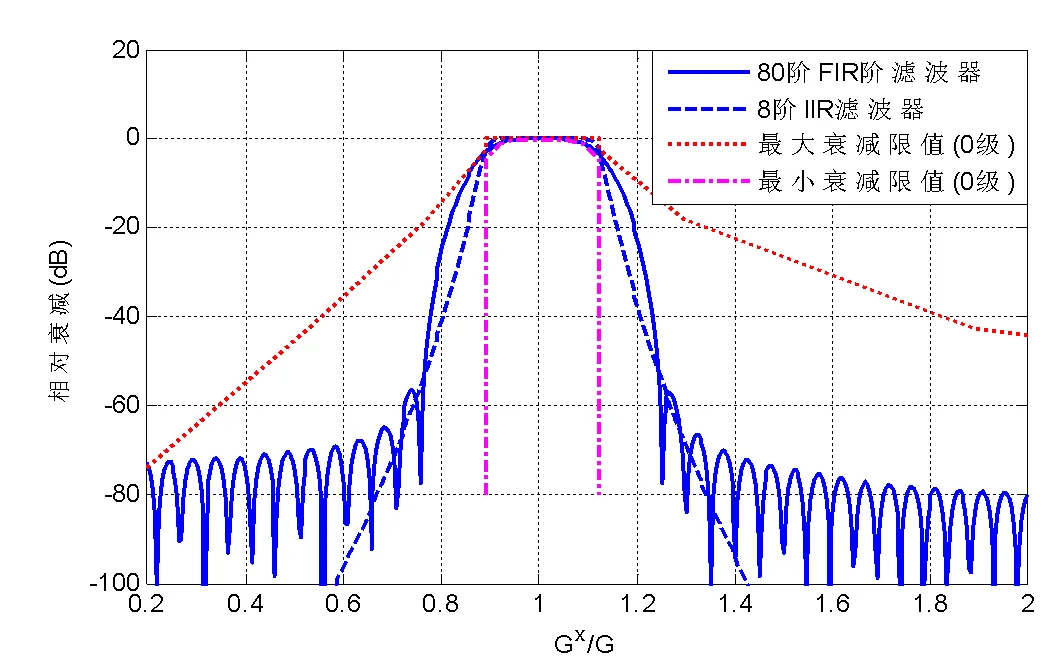
图9 IIR与FIR滤波器比较

在算法成本上有两点进行对比。其一，若使用卷积进行计算，8阶的IIR滤波器需要进行4×8+1次乘法，80阶的FIR滤波器需要进行80+1次乘法，FIR滤波器占用的乘法器资源多；其二，IIR滤波器的系数往往在数值上非常小，运算时需要更长的位数表达，意味着占用比FIR滤波器更多的存储器资源。综上两点，FIR滤波器的算法“成本”比IIR滤波器的算法“成本”略高。但FIR滤波器具有优越的相位性能，为消除叠加后的误差选择使用FIR滤波器。

3 抽样率变换误差分析

初始信号经过低通滤波器后进行抽取和内插，然后再经过低通滤波器，最后通过求和运算得到重组信号。这个过程中产生的信号与理想中的信号存在着误差，主要包括：混叠失真（由抽取和内插产生的混叠和镜像带来的误差所造成）；幅度失真（由滤波器幅频特性波纹产生的误差所造成）；相位失真（由滤波器相频特性非线性产生的误差所造成）[16]。

1）幅度失真：采样序列的频谱成分为0～s/2，当对频率进行1/2抽取时，采样频率减为s/2时可能造成混叠现象，所以在频率抽取之前应先对采样序列进行低通滤波，去掉s/4s/2的频率成分。考虑到低通滤波器同样为FIR滤波器，滤波器要能够很好的表现出低通的效果，通过比较不同窗函数的频响特性，选用了hamming窗。如图10所示，hamming窗同Kaiser窗比较，阻带内有很好的衰减，通带处比较平滑，能够减小序列的幅度失真。

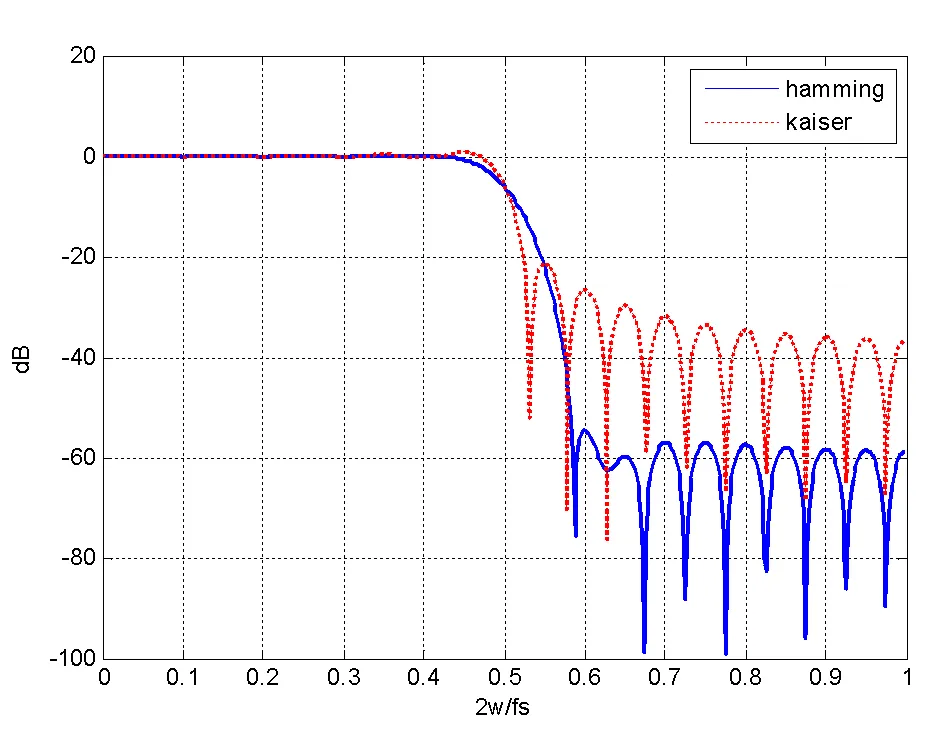
图10 窗函数比较

2）混叠失真：对于两路信号的叠加系统，如图11所示。

图11 两路信号叠加流程

其中

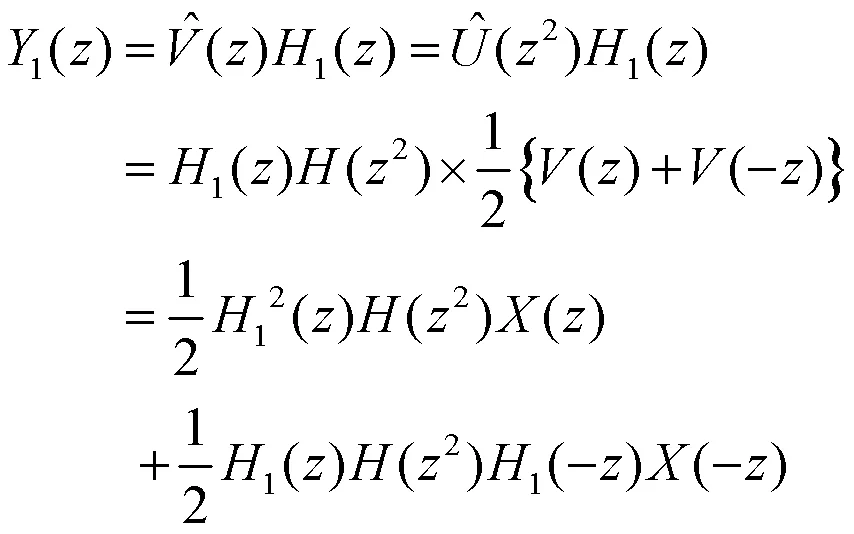
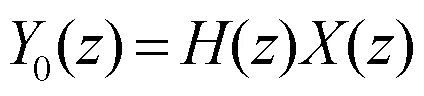
3）相位失真：FIR滤波器的一个突出优点是具有严格地线性相位特性。但并不是所有的FIR滤波器具有这种严格地特性，只有当FIR滤波器单位取样响应满足对称条件时，FIR滤波器才具有线性相位特性。此时系统的群延迟为

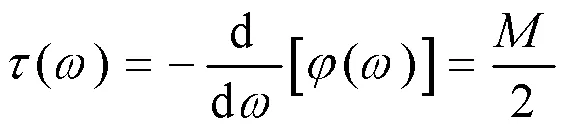
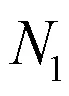
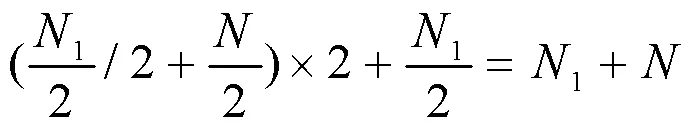
两路信号的差值为

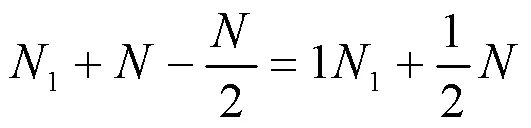
在驱动信号生成过程中，将延迟的点数全部舍弃掉，从延迟后的点开始叠加，能够有效地减小相位失真。

4 试验仿真

为了验证本文算法的可行性，试验仿真采用自闭环控制系统，仿真输入参数如表1所示，全频段参考谱如图12所示。

表1 试验仿真参数

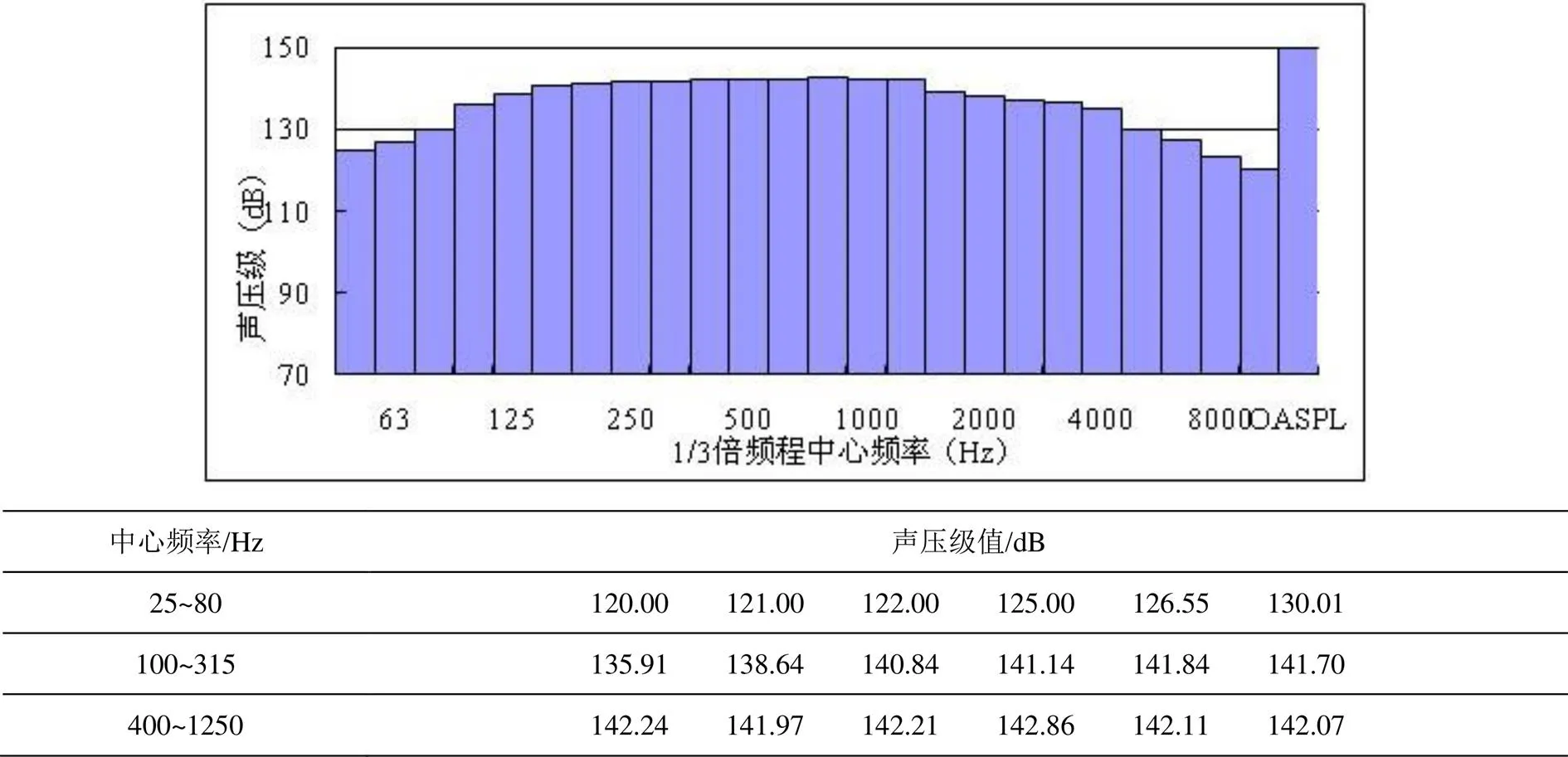
图12 全频段参考谱

仿真结果如图13和图14所示，控制后各频段声压级值如表2所示。通过闭环控制修正各个1/3倍频程的驱动信号，最终输出信号的声压级谱与标准谱比较，其误差范围控制在±0.3dB以内。试验结果表明，误差修正后的滤波器法控制的驱动信号能够满足试验的需求，其控制算法是可行且有效的。

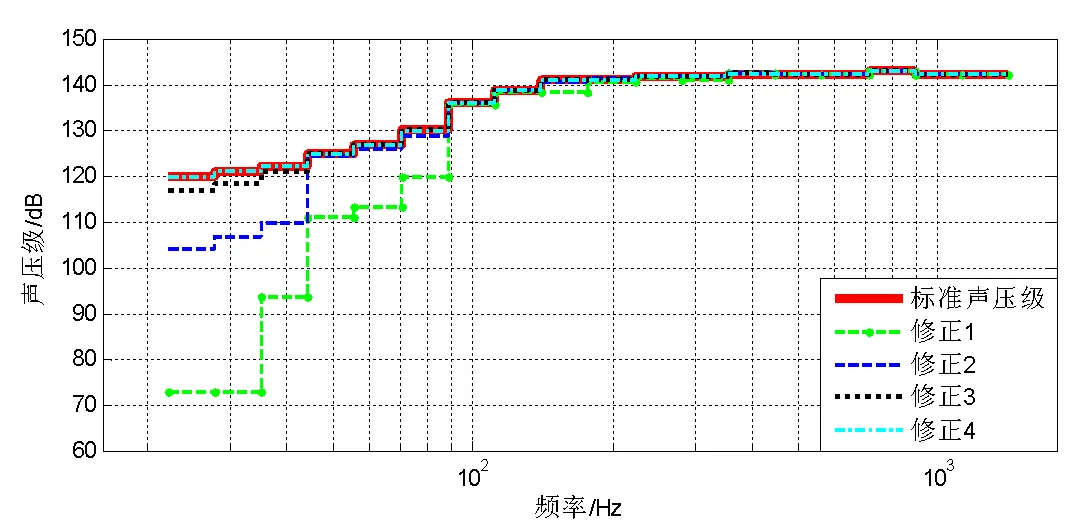
图13 逐渐修正结果

表2 各频段声压级值

图14 修正后的声压级谱

5 结论

本文对噪声试验的声谱控制算法进行了研究，通过对常用控制算法的分析，提出并设计了能够提高实时性和增强低频段控制精度的滤波器方法。该方法通过对不同滤波器的性能比较，选择设计了3个满足国标要求的1/3倍频程FIR滤波器，通过滤波器实现了对一个倍频程频带的实时精确控制，并通过抽样率的变换精确控制了6个倍频程的频率范围。通过误差分析，将信号合成时出现的相位失真和幅度失真等情况进行了优化设计，提高了算法的性能。通过自闭环仿真试验验证了算法的性能和可行性。该控制算法能够利用到噪声试验的声谱控制中，并为控制器的开发提供了算法支撑。

[1] 黄怀德. 振动工程（上）[M]. 宇航出版社, 1993.

[2] 胡志强, 等. 随机振动试验应用技术[M]. 北京: 中国计量出版社, 1996.

[3] 王述成. 振动试验实时控制系统的研究[D]. 浙江大学工学博士学位论文, 2006.

[4] 沈壕. 强噪声环境试验的频谱模拟[J]. 强度与环境, 1997, 24(2): 46-52. [Shen Hao. Simulation of frequency spectrum in high-intencity noise environmental test [J]. Structure & Environment Engineering, 1997, 24(2): 46-52.]

[5] 张利, 高英, 洪利. 高声强混响室噪声试验典型声谱控制方案[J].航天器环境工程, 2011,28(3): 233-237. [Zhang Li, Gao Ying, Hong Li. Typical sound spectrum control of high intensity acoustic reverberation chamber[J]. Spacecraft Environment Engineering, 2011, 28(3): 233-237.]

[6] 杨新峰, 向树红. 噪声试验计算机控制系统研制及调试[J]. 环模技术, 1996(1): 41-46. [Yang Xinfeng, Xiang Shuhong. Development and investigation of computer control system for noise test [J]. Spacecraft Environment Engineering, 1996(1):41-46.]

[7] 杨新峰, 向树红. 噪声试验计算机控制系统[J]. 中国空间科学技术,1997(1): 46-55. [Yang Xinfeng, Xiang Shuhong. Computer-based control system of acoustic testing [J]. Chinese Space Science and Technology, 1997 (1):46-55.]

[8] 张利. 140dB高声强混响室声谱特性分析与试验研究[D]. 上海交通大学工程硕士学位论文, 2012.

[9] 晏廷飞, 方贵前. 声学试验三分之一倍频程控制技术研究[J].航天器环境工程, 2008, 25(5): 463-466. [Yan Tingfei, Fang Guiqian. Research on 1/3 octave acoustic test control technique [J]. Spacecraft Environment Engineering, 2008, 25(5): 463-466.]

[10] Wyle Laboratories Automatic Control System, The control system for acoustic test facilities [G], 1999.

[11] John P Lee, Jerry H. Bosco, A digital control system for high level acoustic noise generation[C], Proceedings of the IESC, 1986.

[12] Stephen D. O’Regan, Bart Burkewitz, Christopher Fuller, Payload noise suppression using distributed active vibration absorbers[C], SPIE Proceedings, 2002(4698): 150-159.

[13] 贺旭东, 陈怀海. 利用FIR滤波器生成随机振动试验驱动信号的新方法[J]. 航空学报, 2003, 24(3): 220-222. [He Xudong, Chen Huaihai. Generating the Driving Signals for Random Vibration Test by FIR Filter [J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(3): 220-222.]

[14] 胡广书. 数字信号处理理论算法与实现（第三版）[M]. 清华大学出版社, 2012.

[15] GB/T 3241-2010, 电声学倍频程和分数倍频程滤波器[S]. 2010.

[16] 陶然, 张慧云, 王越. 多抽样率数字信号处理理论及其应用[M].清华大学出版社, 2007.

Study on Control Arithmetic for Sound Pressure Level Spectrum

WANG Meng WANG Xiao-hui HE Zhi-guo ZHANG Jing

（Beijing Institute of Structure and Environment Engineering, Beijing 100076, China）

Sound pressure level spectrum control is an important part of noise environmental test, and its control refers to the control of octave or 1/3 octave frequency band of sound pressure level. In the control of the current, aiming at the problem of the control precision is not enough at low frequency part and poor real-time performance, a new technique is presented for sound pressure level spectrum control. According to the requirements of GB/T 3241-2010, 1/3 octave filters is designed, and through the characteristics of sound pressure level spectrum division and basic multi-rate operations to propose a filter multiplexing method for real-time system and control arithmetic architecture.

Sound pressure level spectrum control; Signal processing; 1/3 octave filters; Sampling rate conversion

V417+.4

A

1006-3919(2022)03-0058-07

10.19447/j.cnki.11-1773/v.2022.03.009

2021-07-15；

2021-10-22

科技部国家重点研发计划（2021YFB3801700）;重点实验室基金（6142911180512）

王萌（1988—），男，研究生，研究方向：测控系统和产品的开发；（100076）北京9200信箱72分箱.