一种改进的时间最优控制算法∗

刘亚云,金亮亮

(中航工业雷华电子技术研究所，江苏无锡214063)

0 引言

时间最优控制是最优控制理论中的一种，对于非奇异且控制输入变量为线性的一类系统时间最优化问题，采用Bang-Bang控制满足庞特里亚金极小值原理[1]条件。Bang-Bang控制中各分量u∗i(t)为时间t的分段常值函数，并在切换时间上完成两个常值(极大值和极小值)之间的跳变。

在Bang-Bang控制中，如果速度估计的不准确，在开关线附件就会引发控制量的频繁切换，从而引起“颤振”[2]并对实际系统造成很大的损害。本文在开关线两侧设置“缓冲区”，避免了“颤振”，保证系统以最快速度向目标点收敛，并在目标邻域内切换为滑模变结构控制，使系统具有很强的鲁棒性能。

1 系统最优控制设计

雷达伺服系统采取机电控制方式，系统的传递函数[3]简化为

式中，K表示开环增益，T表示惯性时间常数。

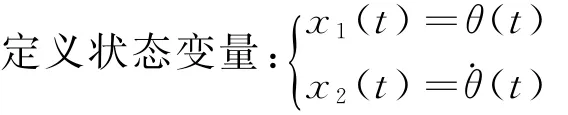
则系统的状态方程为

寻找一个容许控制向量u(t)∈R r，满足

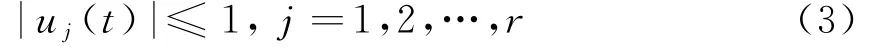
使系统从x(t0)=x0出发，在末态时刻t f到达目标x(t f)=x tf，并使性能指标:

最小。

由极小值原理，构造哈密顿函数:

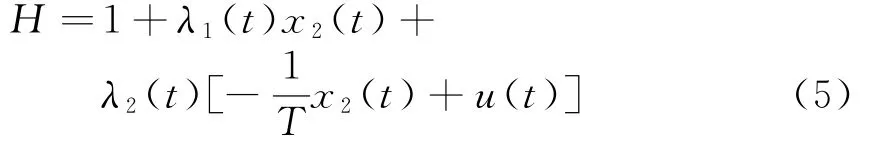
则控制量

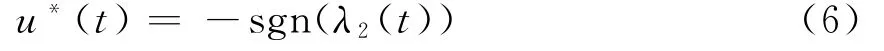
即

在控制量u∗(t)=U作用下，始于(x10，x20)的状态轨线方程为

它在相平面上绘制状态轨迹图如图1所示。

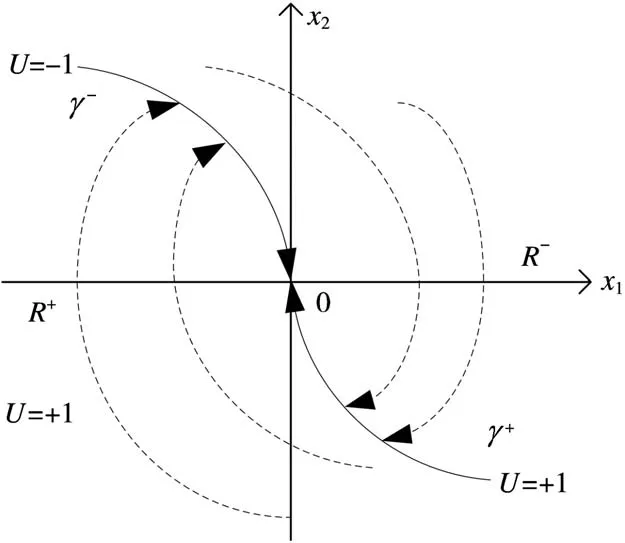
图1 时间最优算法相轨迹图

图1中γ+和γ-组成最优开关线，它们将整个相平面分成R+和R-两部分，设p(x1，x2)为状态空间上任意一点，则最优控制满足如下控制律:

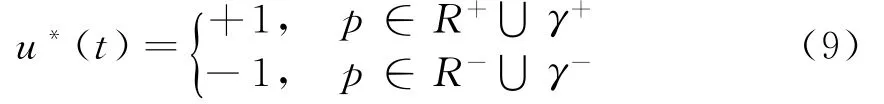
在雷达伺服系统中考虑到减重的需要，一般没有测速电机等可以实时测量电机的角速度，需要采用状态观测器进行估计。由于速度估计不准确，在开关线附近将引发控制量在极大极小值之间频繁切换，产生“颤振”现象。

2 Bang-Bang控制改进算法

为抑制控制量u∗(t)在开关线附近切换形成“颤振”，将开关线在x1轴方向上分别向左、右平移Δx，这样将形成一个宽度为Δx的缓冲区(Δx≤Δx1)，如图2所示。

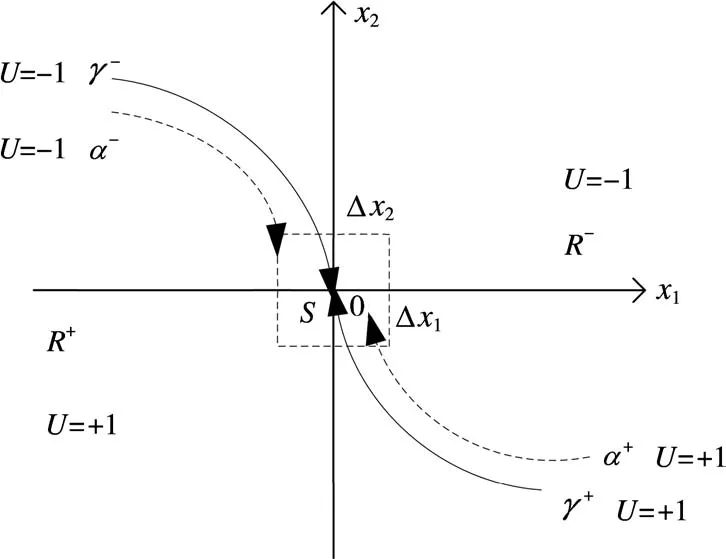
图2 改进后的最优算法相轨迹图

在图2的相平面上，原点附近方框中的区域用S={(x1，x2)||x1|≤Δx1，|x2|≤Δx2}表示，α+和α-为缓冲带，则缓冲带α(即α+和α-)和S将相平面分成R+和R-两部分。设p(x1，x2)为状态空间上任意一点，其控制律为

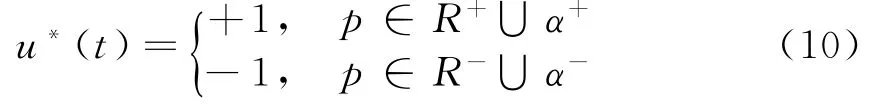
在该算法中，当状态点p(x1，x2)进入开关线后，在开关线附近上下变动时，由于缓冲区的存在，将大大降低控制量来回切换的次数，抑制“颤动”现象。缓冲区的宽度Δx，要根据速度估计误差进行调试。

当状态点p进入区域S时，将切换为滑模变结构控制，这样将避免最优控制算法在原点附近产生“颤振”[4]，同时降低稳态误差，提高定位精度和鲁棒性能。

3 滑模变结构控制算法

滑模变结构控制具有快速响应、对参数变化及扰动不敏感等特点，对最小相位系统和非最小相位系统都具有较好的控制效果[5]。因此，当系统进入滑动模态以后，对外部干扰和参数摄动具有很好的自适应性，基本不受系统参数变化和外界扰动的影响。但是滑模变结构控制在滑动模态下会产生高频抖振，为了减弱抖振，本文使用组合趋近律控制算法，即指数趋近律和变速趋近律的组合。

指数趋近律在稳态时，滑模函数在切换带之间来回切换，产生较大的稳态抖振;变速趋近律稳态时，可稳定于原点，有效地降低了抖振，具有良好的稳态性能。如果把二者结合起来，在滑模运动的前期采用指数趋近律，在滑模运动的后期和稳定段采用变速趋近律[6]，这样系统既能快速趋近，又能降低抖振。

对该系统进行离散化，可得

式中，x(k)=[x1(k)，x2(k)]。 设 指 令 信 号R=[r(k)，dr(k)]，R1=[r(k+1)，dr(k+1)]，切换函数

式中，C e=[c，1]。则

由式(11)、(12)和(13)可得

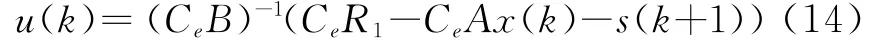
其中离散趋近律为

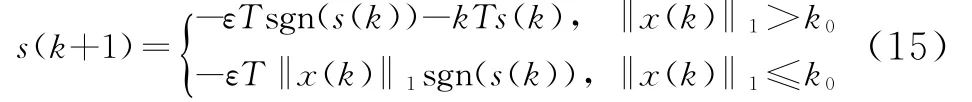
在实际应用中，为了削弱抖振，采用准滑动模态控制原理，即使一定范围内的状态点均被吸引到切换面的某一邻域内，或称为切换面的边界层[7]。因此用饱和函数sat(s)代替滑动模态中的符号函数sgn(s)。

4 试验验证

使用常规的最优控制算法，即不加缓冲区，在1.5 s时指令角度从-90°转换到0°，其角度响应曲线和控制量变化曲线如图3所示。

由图3可知，在2s左右最优控制到达开关线，控制量发生跳转，但在随后的最优运动过程中，控制量在极大极小值之间频繁跳转，产生“颤振”现象，这种“颤振”将对电机造成损害，并影响电机的使用寿命。

使用改进后的最优控制算法，指令在1.6 s左右从0°跳转到-90°，当状态点进入区域S时，分别使用PID控制算法和滑模变结构控制算法，其控制效果如图4和图5所示。

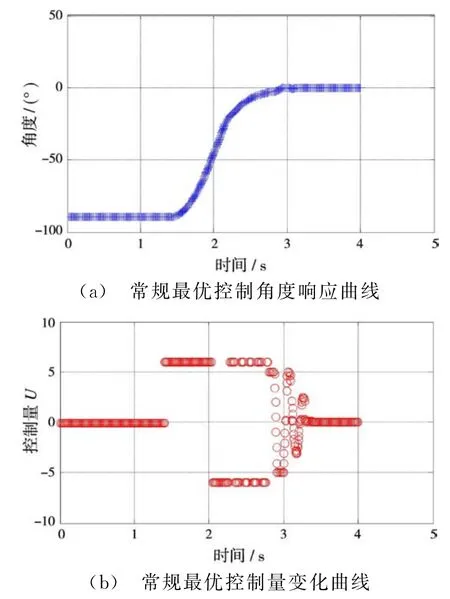
图3 常规最优控制效果图

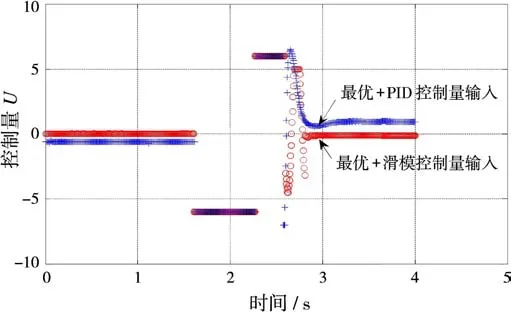
图4 控制量输出比较图

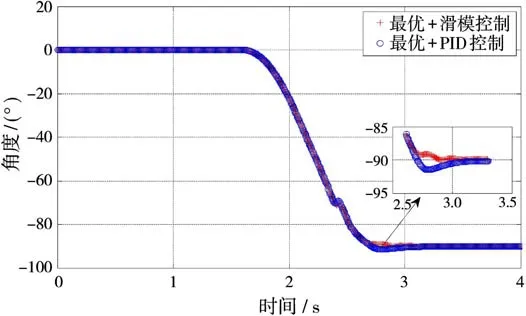
图5 角度响应曲线比较图

由图4可知，在2.3s左右控制量发生跳转，并且在整个运动过程中只跳转了一次，有效避免了控制量在开关线附近频繁的切换，大大降低了“颤振”对系统造成的危害。

由图5可知，常规PID控制超调量为1.48°，3.2 s时进入稳态，稳态误差为0.2°。而滑模控制为欠阻尼，3 s时进入稳态，稳态误差为0.07°。

由比较结果可知，滑模控制的稳态性能优于常规PID控制，并且滑模控制算法鲁棒性能强，对于电机参数变化等具有一定的抗干扰能力。

5 结束语

仿真和实践表明，在缺乏测速传感器以及速度有较大的干扰情况下，改进最优算法结合滑模控制算法有效地解决了控制律“颤振”及稳态误差的问题。从图3～图5可以看出，使用改进后的最优控制算法后，控制律从进入开关线开始到接近目标点过程中，没有发生切换，避免了“颤振”现象的发生。进入目标点邻域后使用滑模变结构控制算法，降低了系统的稳态误差，提高了定位精度和鲁棒性能。

改进后的时间最优和滑模变结构组合控制算法，能使系统以最短的时间运动到目标点并能保持很好的稳定性和控制精度。

[1]胡寿松，王执铨，胡维礼.最优控制理论与系统[M].北京:科学出版社，2010:68-74.

[2]丁青青，王赞基.时间最优控制算法及其在SVC中的应用[J].清华大学学报，2004，44(4):442-445.

[3]李凤俐.时间最优控制理论在雷达伺服系统中的应用[J].测控技术，2008，27(6):47-49.

[4]徐凯.一种时间最优参数自调整模糊矢量控制方法的研究[J].控制与决策，2010，25(1):153-156.

[5]唐茂华，吴鹏.基于自抗扰的非最小相位伺服系统控制[J].雷达科学与技术，2013，11(3):335-340.TANG Mao-hua，WU Peng.Control of Non-Minimum Phase Servo System Based on Auto Disturbance Rejection[J].Radar Science and Technology，2013，11(3):335-340.(in Chinese)

[6]刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社，2005:93-95.

[7]李义强，周惠兴，王先逵，等.直线电机伺服定位系统时间最优鲁棒控制[J].电机与控制学报，2011，15(3):13-18.