极化阵列雷达单脉冲测角方法研究∗

黄艳刚,徐振海,戴 崇,熊子源

(国防科技大学电子信息系统复杂电磁环境效应国家重点实验室，湖南长沙410073)

0 引言

极化阵列雷达能够准确获取目标的极化信息，并通过阵列信号处理提高雷达抗干扰、分辨多目标、遂行多任务的能力，是当前雷达发展的主流之一。美国于2006年立项研制多功能全极化有源相控阵雷达(MPAR，Multiple Function Phased Array Radar)[1]，通过变换极化方式更好地监测天气和服务国防安全。其现役弹道导弹防御系统的核心——X波段地基防御雷达系统(GBR)也是具有全极化测量能力的相控阵雷达[2]，据悉利用极化信息可完全识别真假弹道目标[3]。国内外研究表明，极化阵列雷达在抗干扰[4-5]、目标识别[6-7]、成像[8]等方面明显优于传统单极化阵列雷达。国防科大徐振海研究证明极化敏感阵列在滤波、检测、参数估计三个方面具有巨大应用潜力[9-10]。

测角是雷达最基本的任务之一，其在极化阵列雷达上的实现方法及性能评估鲜有文献报道。就最常用的单脉冲方法而言，其技术应用随雷达体制的发展不断进步。机械扫描雷达中，最早单脉冲技术通过比较在抛物面天线焦点处放置4喇叭馈源形成的对称4个波瓣的接收信号来实现[11]。经典的单脉冲可分成“幅度比较”和“相位比较”两种基本类型，通过比较两个或多个波束接收信号的幅度或相位差异来获得目标角度信息[12]。相控阵雷达中，由于采用阵列天线，单脉冲技术不用明确地区分为“比幅”还是“比相”。其主要通过计算阵列信号处理形成的和差输出比值获得目标角度信息。文献[13]详细论述了对阵元的和差加权准则以及对应的测角公式，并证明了测角性能因采用多阵元的阵列天线而得到显著提高[14]。极化阵列雷达中增加了极化信息，其对单脉冲实现方法的影响及由此得到的测角性能得益值得深入研究。

为此本文基于极化阵列雷达提出了采用极化并联的单脉冲测角方法并分析了其测角性能。

1 极化阵列雷达接收信号模型

本文以双正交偶极子对构成的一维线阵为例介绍方法原理，极化阵列可推广到实际工程中复杂多变的结构。

极化阵列结构如图1所示。N个正交偶极子对沿Y轴均匀排列，阵元间距为d。阵元的两个正交偶极子分别沿X轴和Y轴排列。定义X为水平极化，Y为垂直极化。阵元为理想阵元且满足短阵子假设，即偶极子的长度远小于最大工作频率对应的半波长，接收电压与偶极子所在方向电场成正比。

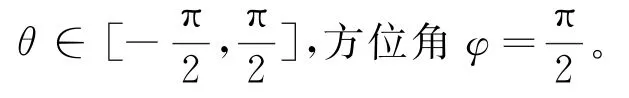
图1 阵列结构示意图

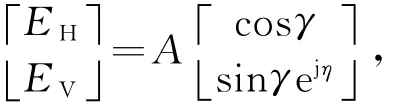
得到的水平和垂直极化阵列接收信号为

式中，nH，nV∈C N×1表示接收机复噪声，通常认为各接收通道内的噪声为独立的高斯白噪声，即信噪比定义为s(θ)为阵列导向矢量:

以第一个阵元为参考阵元，则第n个阵元接收信号相对参考阵元的空间相位滞后为ϕn=-2π(n-1)dsinθ/λ。

2 基于极化并联的单脉冲测角方法

本节详细介绍基于极化并联的单脉冲测角方法，并分析其测角性能，给出了测角性能与SNR及回波极化角的关系。

2.1 处理流程

基于极化并联的单脉冲测角方法处理流程如图2所示。根据接收信号模型，极化阵列雷达可以简单地看成两个不同单极化阵列雷达的组合。根据单脉冲原理和最大似然估计，分别获得不同极化部分角度测量和幅度估计，再对来波信息进行加权融合得到最终角度测量。

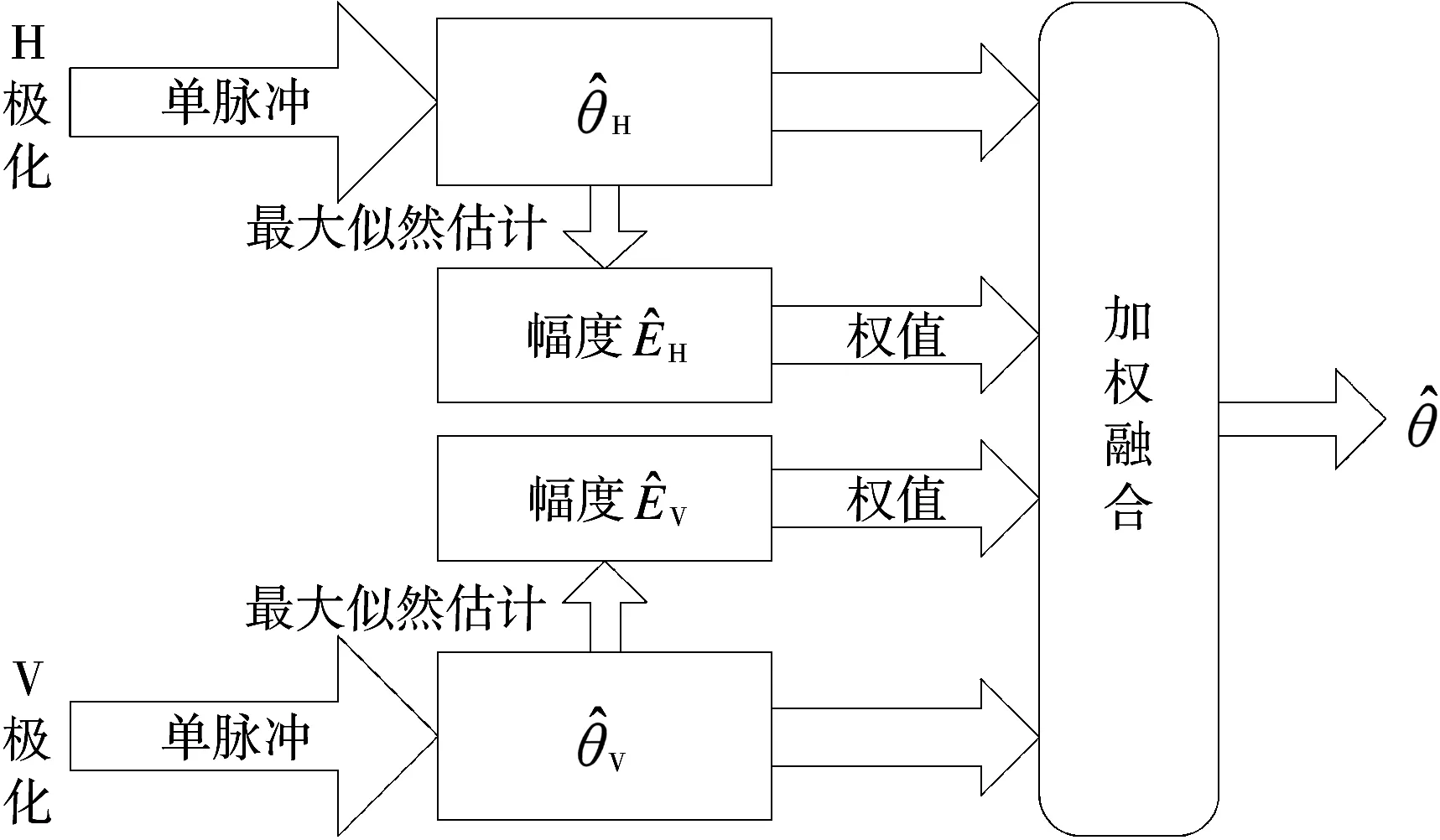
图2 基于极化并联的单脉冲方法处理流程

2.2 单脉冲测量与幅度估计

对H和V极化阵列部分分别独立使用单脉冲测角技术，得到角度测量值本文采用相位和差单脉冲方法，将一维线阵平分为两个子天线阵。这两个天线阵波束指向一致，得到两个一样的接收波束，只是相位中心间距则两波束接收信号幅度相等，相位相差两波束输出信号记为E1，E2，则E2=E1eiΔφ。通过计算差和比即可提取目标角度信息。

经推导，其测角公式为

式中，θ0为波束指向，Δ=dH(θ0)x为差波束输出，Σ=sH(θ0)x为和波束输出。

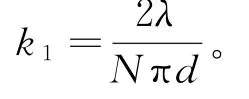
图3给出了16元阵的和、差波束幅度权分布图。图4给出了对应的鉴角曲线，可以看出在波束宽度内，该鉴角曲线具有较好的线性。

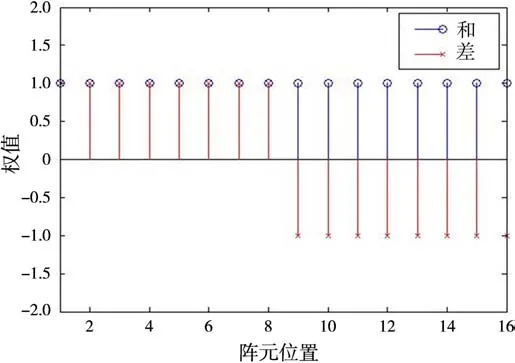
图3 和、差波束幅度权分布图(N=16)

图4 鉴角曲线

在得出角度测量值^θH，^θV的基础上，由最大似然估计方法得到H和V极化方向复幅度。以水平极化为例，接收信号模型改写为

其概率密度函数(PDF)为

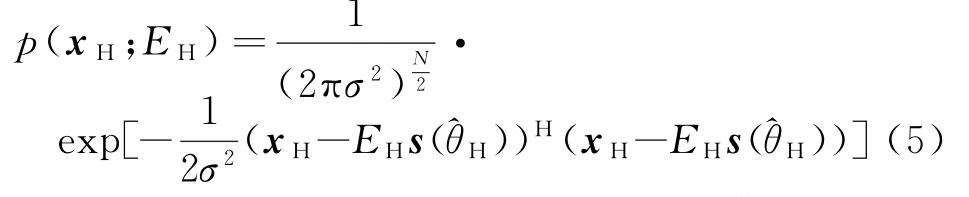
最大似然函数方法求解得到接收信号在水平和垂直极化方向复幅度的估计值:

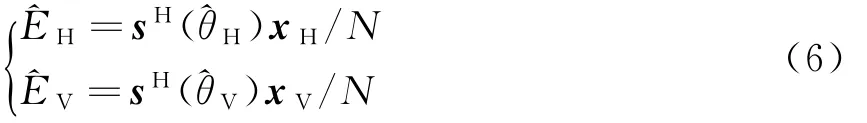
2.3 加权融合

最后，将 H和 V极化的角度测量值^θH，^θV进行融合，得到目标最终角度估计^θ。采用加权融合[15]，即

优化加权系数α1，α2使^θ的方差σ2最小化，通过Lagrange乘子法求解得

式中，k2为常数，θ3dB为3 d B波束宽度。得最终角度估计值:

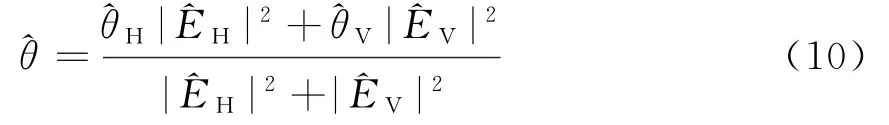
3 理论性能分析

该加权融合方式物理意义明确:功率越大的极化部分角度测量值可靠性越高，权重应该越大。

由式(7)、(8)得

由式(11)可知，σ2分别小于σ2H和σ2V，说明了基于极化并联方法的测角性能优于单极化。联立式(9)、(11)，得

式(12)说明了基于极化并联的单脉冲方法测角性能与SNR、波束宽度和回波极化状态的关系。结果表明:角度估计精度与SNR成反比，与波束宽度成正比，但与回波极化状态无关。

4 仿真验证

本节仿真验证极化并联方法的测角性能，并与单极化阵列的测角性能进行对比。仿真给出了估计精度与SNR及回波极化状态关系。

仿真设置:阵元数N=16，阵元间距半波长。波束指向θ0=0°，蒙特卡洛次数M=1 000。

4.1 估计精度与SNR的关系

图5给出了三种回波极化状态下，不同方法的RMSE与信噪比的关系曲线，其中仰角θ=0°。从图5可以看出，测角性能随着信噪比增高而提升，而且对于任意给定的回波极化状态，本文方法测角性能都优于单极化阵列单脉冲方法。

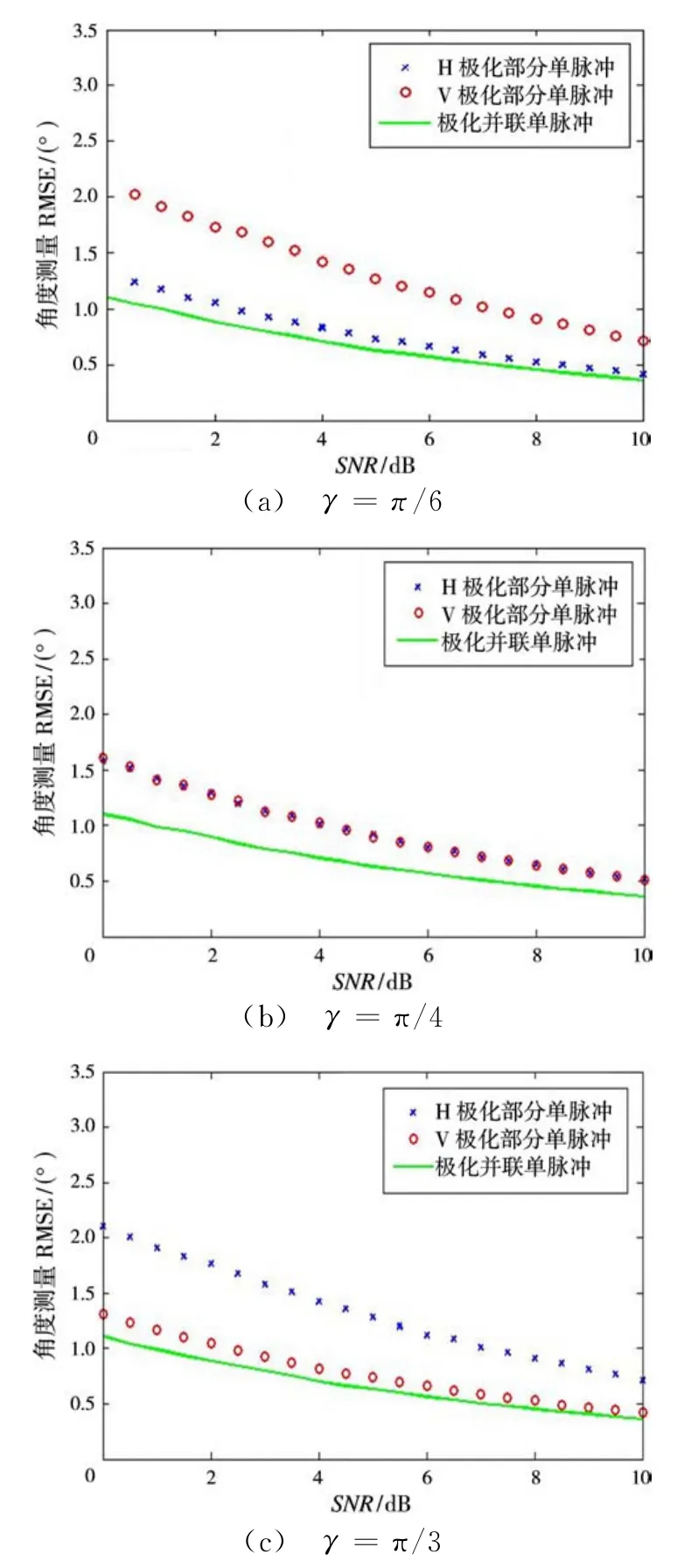
图5 RMSE与SNR的关系

4.2 测角精度与回波极化角的关系

图6 给出了RMSE与极化角γ的关系，其中相关参数为:SNR=10 d B，仰角θ=0°。从图6看出:单极化阵列测角方法敏感于极化状态的变化，且不同极化状态下测角性能相差较大;而基于极化并联的单脉冲方法测角性能不随极化状态改变而改变。说明了本方法较单极化阵列测角具有更好的适应性。

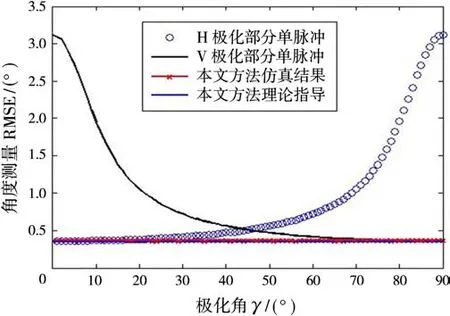
图6 RMSE与极化角γ的关系

5 结束语

本文对极化阵列雷达的单脉冲测角方法进行了研究，并对测角性能进行了分析。理论分析和仿真验证表明:极化阵列单脉冲测角性能优于单极化阵列，且测角性能与回波的极化状态无关，较单极化阵列测角具有更好的适应性。本文提出的基于极化并联的测角方法在极化阵列雷达中具有应用潜力，本文的研究工作可以为极化阵列雷达测角工程实践提供参考。

[1]HERD J，CARLSON D，DUFFY S，et al.Multifunction Phased Array Radar(MPAR)for Aircraft and Weather Surveillance[C]∥2010 IEEE Radar Conference，Washington，DC:[s.n.]，2010:945-948.

[2]FETTER S，ANDREW M S，JOHN M C，et al.Countermeasures:A Technical Evaluation of the Operational Effectiveness of the Planned US National Missile Defense System[C]∥Union of Concerned Scienst，Cambridge，MA:[s.n.]，2000.

[3]863先进防御技术通讯(A类).美国国防部声称NMD能够识别真假目标[J].863先进防御技术通讯简讯，2000(14):1-2.

[4]BRANDES E A，ZHANG Guifu，VIVEKANANDAN J.Experiments in Rainfail Estimation with a Polarimetric Radar in a Subtropical Environment[J].Jour-nal of Applied Meteorology，2002，41(6):674-685.

[5]PASTINA D，LOMBARDO P，PEDICINI V，et al.Adaptive Polarimetric Target Detection with Coherent Radar[C]∥IEEE International Radar Conference，Alexandria，VA:[s.n.]，2000:93-97.

[6]COMPTON R T.On the Performance of a Polarization Sensitive Adaptive Array[J].IEEE Trans on Antennas and Propagation，1981，29(5):718-725.

[7]王福友，罗钉，刘宏伟.基于极化不变量特征的雷达目标识别技术[J].雷达科学与技术，2013，11(2):165-172.

[8]CLOUDE S R，CORR D G，WILLIAMS M L.Target Detection Beneath Foliage Using Polarimetric Synthetic Aperture Radar Interferometry[J].Waves in Random Media，2004，14(2):393-414.

[9]徐振海.极化敏感阵列信号处理研究[D].长沙:国防科技大学电子科学与工程学院，2004.

[10]徐振海，王雪松，肖顺平，等.极化敏感阵列滤波性能分析:完全极化情形[J].电子学报，2004，32(8):1310-1313.

[11]王德纯，丁家会，程望东.精密跟踪测量雷达技术[M].北京:电子工业出版社，2006.

[12]SHERMAN S M，BARTON D K.Monopulse Principles and Techniques[M].Norwood:Artech House，1986.

[13]NICKEL U.Overview of Generalized Monopulse Estimation[J].IEEE Aerospace and Electronic Systems Magazine，2006，21(6):27-56.

[14]Nickel U.Generalised Monopulse Estimation and Its Performance[C]∥Proceedings of the 3rd IEEE International Symposium on Signal Processing and Information Technology，Darmstadt，Germany:[s.n.]，2003:174-177.

[15]夏佩伦.目标跟踪与信息融合[M].北京:国防工业出版社，2010.

[16]张光义.相控阵雷达原理[M].北京:国防工业出版社，2009.