一种基于多相滤波的高速信号处理算法∗
2014-03-21吕影影崔志超
吕影影,徐 强,崔志超
(1.电子科技大学通信与信息工程学院,四川成都611731;2.电子科技大学通信抗干扰技术国家级重点实验室,四川成都611731)
0 引言
多速率信号处理在数字信号处理系统中有着广泛应用,因为它便于信息编码、传输和存储,可以节省系统资源以及实现不同速率要求系统的兼容[1]。内插即增大信号的采样率以增加数据冗余,抽取即降低信号的采样率以减少数据冗余,它们都是在保证信号不失真的前提下改变信号的采样率。内插或抽取的倍数越大,对滤波器阶数的要求越高[2],信号处理的运算量越大,实现越困难。对于高速率信号,经过多级内插后,采样率将远远大于系统时钟频率,在工程中,受硬件条件如滤波器、FPGA时钟频率、资源等的约束,使实现更加困难[3-4]。
针对采样率变换系统,在单级内插多相滤波结构的基础上,以多级内插处理为例进行公式推导及仿真验证,在不改变系统时钟频率的条件下,通过多路低采样率信号等效实现高采样率信号,并在接收端分析了信号合成的过程。提出了一种基于多相滤波的多速率处理算法,提供了一种实现高速率信号发送及接收的解决方案。
1 信号经过多相滤波器的多相分解
在多速率信号处理中,多相滤波的核心思想就是滤波和整数倍的采样速率转换在一个级联结构中分段实现。基于多相滤波器结构将信号进行多相分解,即将一路高采样率信号分为几路低采样率的信号[5-6]。
内插系统有单级实现和多级实现两种等效的方式,内插系统结构如图1所示。
若I=4,I1=2,I2=2,则图1的结构可用图2所示的级联内插等效表示。
1.1 单级内插时信号的多相分解
图2 中,设内插前的信号为x(n),内插倍数为2,若x(n)序列为
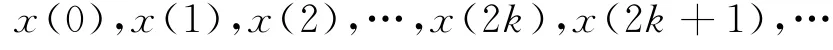
则第一级内插后的信号x1(n)为

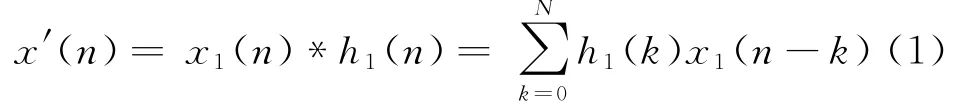
N为使h1(k)x1(n-k)有意义的项,以下含义相同。
设x′0(n)为x′(n)的偶数项,x′1(n)为x′(n)的奇数项。则
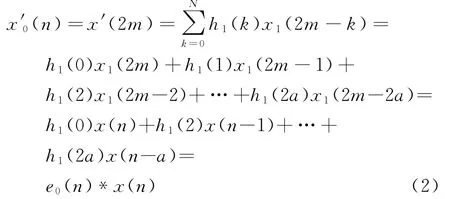
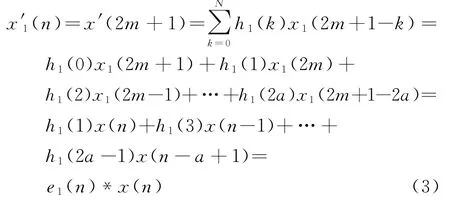
由上述公式推导,可以看出不通过直接内插滤波的方式,而是通过多相滤波可以将采样率为2fs的信号x′(n)分解为两路采样率为fs的x′0(n),x′1(n)信号,如图3所示。

图3 信号通过多相滤波的两相分解
同理,可将h1(n)分为I相,经过多相滤波可以将采样率为Ifs的高速信号x′(n)分解为I路采样率为fs的信号,如图4所示。

图4 信号通过多相滤波的I相分解
这种分解方式可以用于由多个谱宽相同、中心频率间隔均匀的窄带信号组成的宽带多通道信号的分离。例如,用于信号压缩和语音传输的分频带编码信号。
1.2 级联内插时信号的多相分解
图2中,x′(n)为第一级内插并滤波后得到的信号,设经过内插2倍后的信号为x2(n),则
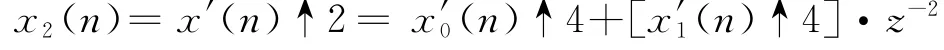
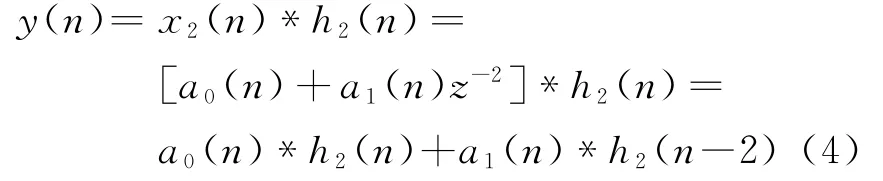
设h2(n)分为四相:

由图4得a0(n)∗h2(n)可以分解为四相信号

同理,a1(n)∗h2(n-2)可以分解为以下四相信号:x′1(n)∗g2(n)z-1,x′1(n)∗g3(n)z-1,x′1(n)∗g0(n),x′1(n)∗g1(n);延时是为了与第一项a0(n)∗h2(n)的值相对应。则y(n)可分解为四相:y0(n),y1(n),y2(n),y3(n)。
第一相
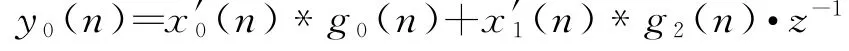
第二相

第三相
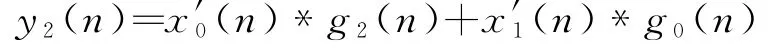
第四相
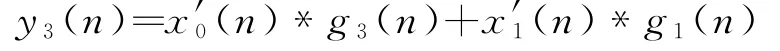
级联内插时信号的多相分解如图5所示,通过级联多相滤波结构将采样率为4fs高速信号y(n)分解为四路采样率为fs的信号。
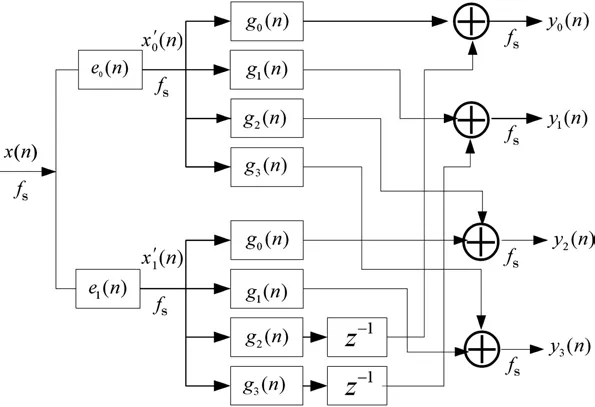
图5 级联内插时信号的多相分解
可以通过上述原理分析其他内插倍数的级联结构时信号的多相分解。需要注意的是信号及滤波器分解的相数与可以采用的通道数目和输入采样率有关。
2 基于多相滤波器的信号合成
将信号进行多相分解并经多通道发送后,在接收端需要将多路信号合成为一路。以图2中级联内插结构的逆过程为例分析信号合成过程,如图6所示。

图6 内插系统的级联结构
由1.2节知,y(n)可分解为四相:y0(n),y1(n),y2(n),y3(n),它们分别经过两倍内插后的信号依次为y′0(n),y′1(n),y′2(n),y′3(n),分 别 经 过四倍内插后的信号依次为y″0(n),y″1(n),y″2(n),y″3(n),则
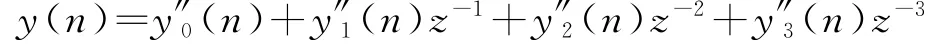
若y(n)分解为两相信号,设其分别为b0(n),b1(n);h2(n)分解为两相信号e0(n),e1(n),则

由上述推导,得[y(n)∗h2(n)]↓2的信号值可以由y(n)两相分解后的两路信号与h2(n)两相分解后的两个滤波器对应作卷积运算得到。
另外,
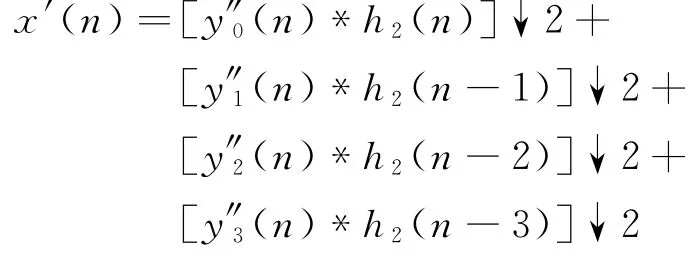
对于第一项,y″0(n)可以分解为y′0(n)与一个全0序列,即y″0(n)分解后的第二相信号与h2(n)分解后的第二相波波器e1(n)卷积和为0。所以,[y″0(n)∗h2(n)]↓2的信号值即为的值;同理,第二项、第三项、第四项的值分别为[y′1(n)∗e1(n)]z-1,[y′2(n)∗e0(n)]z-1和[y′3(n)∗e1(n)]z-2。延时是为了使各项的值对应相加,即

e0(n)两相分解后分别为g0(n),g2(n);e1(n)两相分解为g1(n),g3(n),按照式 (2)、(3),y′0(n)e0(n)即为[y0(n)↑2]∗e0(n),可以分解为y0(n)∗g0(n)和y0(n)∗g2(n),以此类推对每项两相分解后,得
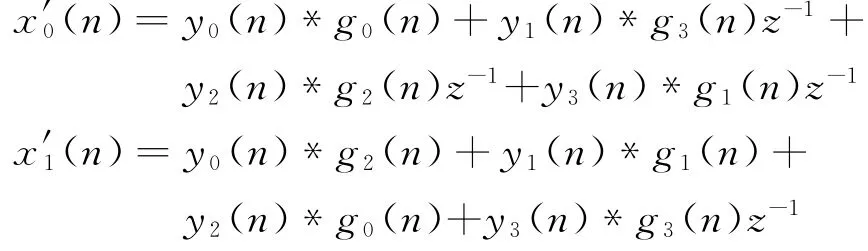
上述推导如图7所示。
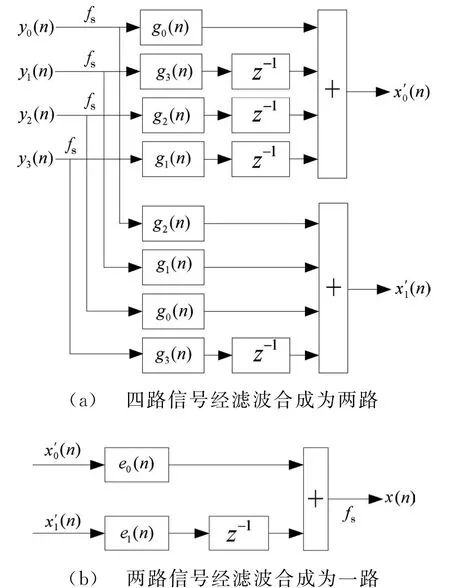
图7 基于多相滤波的信号合成
可以按照上述算法得到其他抽取倍数的级联结构时信号的合成。
3 仿真结果
为验证上述推导的正确性,以802.11ac协议为依据,产生中心频率为零、带宽为160 M Hz、速率为160 MS/s的信号,如图8所示(增益模块是为了功率归一化)。
以原始信号(图8)作为第一路波形,将信号通过图2与图6所示结构级联起来得到的波形作为第二路,如图9(a)所示,h1(n)为半带滤波器,阶数为800,通带截止频率为78.6 MHz,h2(n)为半带滤波器,阶数为60,通带截止频率为100 MHz。
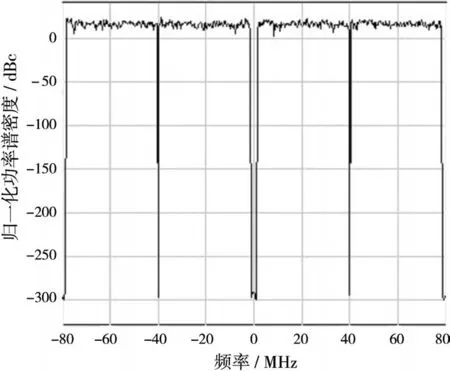
图8 信号源产生及其频谱图
将信号通过图5与图7所示结构级联起来得到的波形作为第三路,如图9(b)所示,e0(n),e1(n)滤波器系数分别为h1(n)的奇数项与偶数项,阶数分别为200和399;g0(n),g1(n),g2(n),g3(n)分别为h2(n)的第一相、第二相、第三相和第四相,阶数分别为0,14,7,14(半带滤波器有一半系数为0,分多相后存在系数全为0的滤波器)。
考虑到信号经过滤波器的时延,将输入原始信号作相应延时后三路数据波形对比如图10所示。
如图10所示,同一时刻三路波形相同,说明图9(a)与图9(b)所示原始信号经过不同处理后的信号是等效的;即通过基于多相滤波结构将信号进行多相分解与合成,可以等效实现通过内插与抽取改变信号采样率的过程。且基于多相滤波结构的信号处理过程中,信号的采样率一直不变,高阶数的滤波器可以通过分多相后的低阶滤波器等效实现,工程实现时大大降低了系统时钟大小的限制,及对滤波器的要求,易于实现[7]。
4 结束语
采样率变换系统中,采用多级多相滤波处理,实现了在低采样率的条件下,得到高采样率的输出信号,而且降低了实现中高速率信号对系统时钟频率的要求。并用仿真结果证明了这种基于多相滤波结构的信号多相分解与合成的可行性和高效性,可广泛用于宽带信号数字上变频、下变频等多速率信号处理系统。
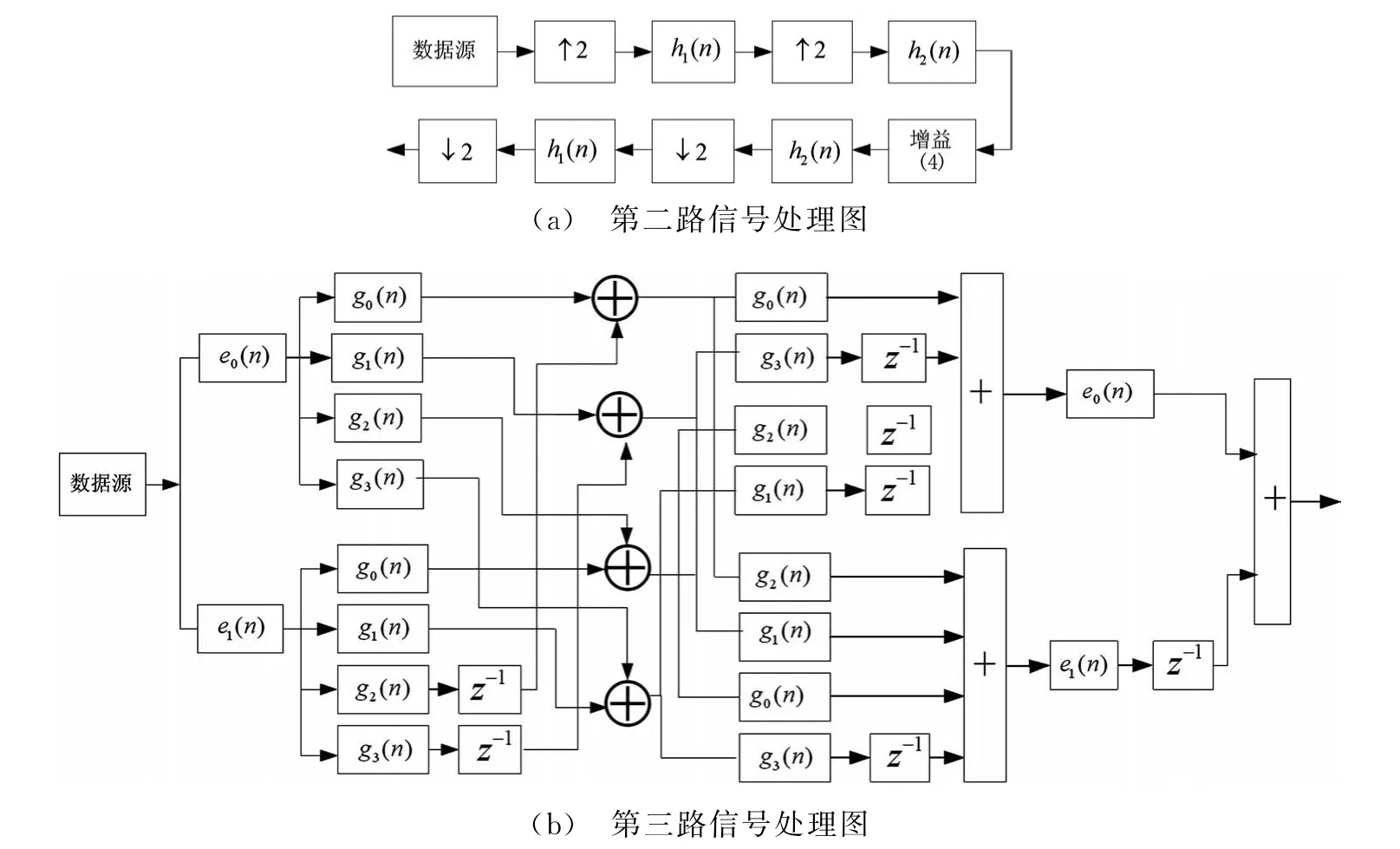
图9 原始信号经不同形式处理的框图
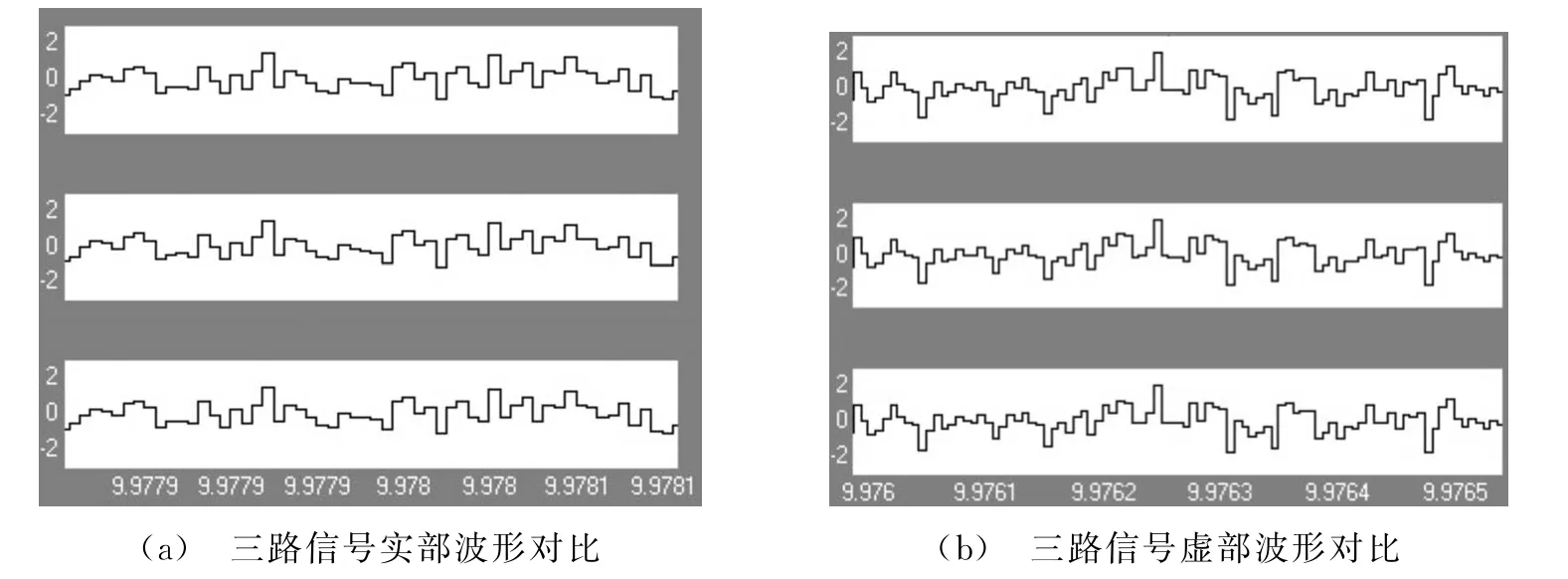
图10 三路信号波形对比
[1]陈祝明.软件无线电技术基础[M].北京:高等教育出版社,2007:81-89.
[2]杨小牛,楼才义,徐建良.软件无线电原理与应用[M].北京:电子工业出版社,2001:21-87.
[3]黄磊.基于多相滤波结构的整数倍内插技术[J].无线电工程,2011,41(5):62-64.
[4]董晖,姜秋喜,毕大平.多相滤波宽带信道化数字接收机[J].雷达科学与技术,2007,5(1):73-77.DONG Hui,JIANG Qiu-xi,BI Da-ping.Polyphase Filtering Wide-Band Channelized Digital Receiver[J].Radar Science and Technology,2007,5(1):73-77.(in Chinese)
[5]VAUGHAN R G,SCOTT N L,WHITE D R.The Theory of Bandpass Sampling[J].IEEE Trans on Signal Processing,1991,39(9):1973-1984.
[6]MITOLA J.The Software Radio Architecture[J].IEEE Communications Magzine,1995,33(5):50-55.
[7]侯聪.多相滤波数字信道化的FPGA实现[J].电讯技术,2012,52(8):1345-1348.
