复杂阵地米波雷达低仰角测高算法研究∗

宋秀芬,朱 伟,谢腾飞,马晓静

(1.中国电子科技集团公司第三十八研究所，安徽合肥230088;2.解放军电子工程学院，安徽合肥230037)

0 引言

在现代战争中随着飞行技术的不断发展，敌方飞机和导弹越来越多地利用地形作为掩护，采取低空突防的方式对阵地进行攻击，其主要特点是飞行高度低，飞行速度快，雷达反射面积小，机动性强，利用地、海杂波和多径效应以及地形、地物的遮挡来躲避雷达和防空武器，这就对雷达提出准确的测量、跟踪低空飞行目标的要求。米波阵列雷达由于波束较宽，地/海面反射波是不可避免的。在测量低空目标高度时，地形起伏对测量结果的影响很大，崎岖的地表、建筑物以及山脉等反射面或强海情海面等这些非平坦、不规则的反射面对测高的影响非常大。

针对米波雷达低仰角测高的问题已进行了大量的研究。早期的方法主要有多频平滑法、空域滤波法、复指示角技术、相关高度法和距离高分辨等测高方法。近年来阵列超分辨技术已应用于低仰角雷达测高，主要集中在两个方面:一是特征子空间类算法;二是最大似然(ML)类参数估计方法。但是这些超分辨算法在直达角和反射角的夹角小于波束宽度的1/4时，无法进行分辨[1]。文献[2]建立精确多径反射信号模型，提出基于精确多径反射信号模型的最大似然算法。文献[3]基于特征矢量的测高算法，并给出了某雷达的实验结果;文献[4]研究基于地形参数-角度二维搜索的合成导向矢量MUSIC和ML算法;文献[5]提出与阵列几何模型匹配的最大似然阵列超分辨测高方法。以上方法适用的前提是，多径反射面较为平坦或者起伏不大，对任意仰角，所有阵元接收的反射波为点目标，而且各阵元接收的地面反射分量的入射角近似认为相等。

但是在较复杂的阵地，比如崎岖的地面、强海情的海面等起伏较大的反射面(反射面的起伏达到波长的数倍)，此时地面粗糙度增加到不能满足瑞利准则[6]，多径信号不是完全镜面反射，而应该是镜面反射分量与漫反射分量之和，反射面越粗糙，雷达仰角越低，漫散射功率越占主导地位。即多径信号的能量在空间形成一定的分布，此时多径信号应该为分布源，在这种情况下现有方法均难以得到较好的测高效果。针对以上问题，本文首先建立多径服从分布源的阵列信号模型，然后利用多维交替投影算法来估计模型中的参数，最后给出仿真和实测数据结果。

1 信号模型

考虑一个远场窄带信号入射到垂直放置的M个各向同性阵元组成的均匀线阵，图1是在复杂阵地下低仰角区测高环境中的几何框图(不考虑地球曲率)。其中hr为雷达天线中心架高，ht为目标高度，Rd为目标相对雷达的直达距离，Ri为目标由地(海)面反射的多径距离，直达波为点目标，θd为直达波入射角，多径信号为分布源，θi为多径信号中心反射角，Δ为分布源参数。

图1 复杂阵地下米波雷达低仰角测高模型

阵列的输出信号矢量为

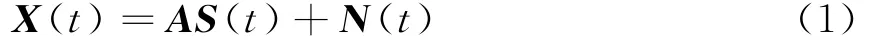
式中，X(t)为各阵元的接收数据;N(t)为零均值，方差为σ2的复高斯白噪声，各阵元输出 噪声统 计 独 立;S(t)=[s(t)，ρs(t)]为信号矢量，其中ρ为地面反射系数;A=[a(θd)，b(θi，Δ)]为导向矢量，其中a(θd)=[1，a(θd)，…，a m(θd)，…，a M-1(θd)]T(m=0，1，…，M-1)为直达波的导向矢量，上标T表示转置，a(θd)=exp(jκdsin(θd))，κ=2π/λ为波数;b(θi，Δ)为多径信号的导向矢量。

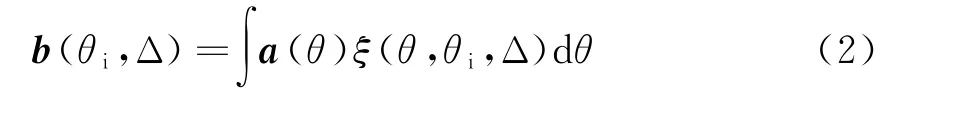
式中，ξ(θ，θi，Δ)为角分布函数。

在此假设地面多径反射服从高斯分布源模型，即角分布函数为高斯函数。

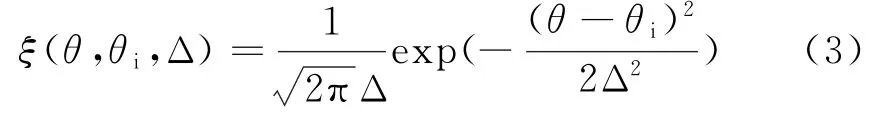
图2给出不同参数下的服从高斯分布的角信号分布函数。

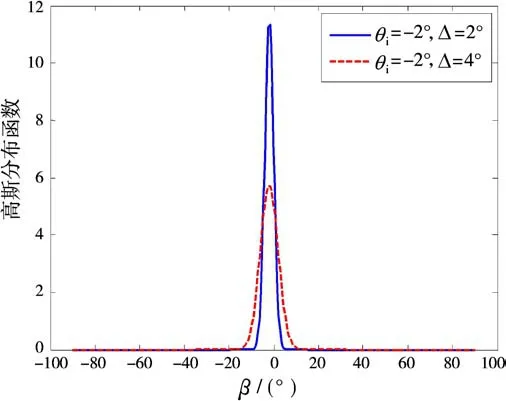
图2 角分布函数

将式(3)代入式(2)得到

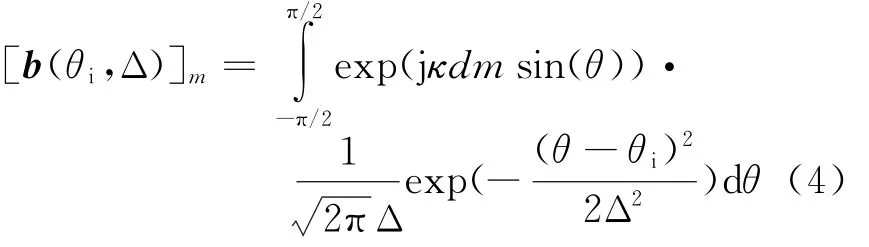
对式(4)进行近似[7]

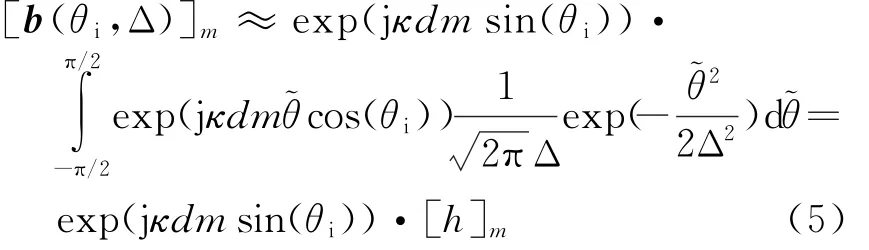
式中，

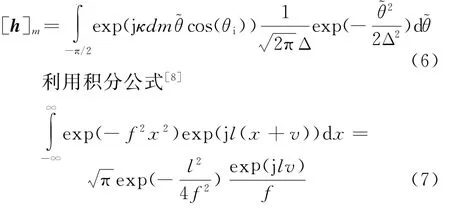
式(5)可以得到闭式表达式:

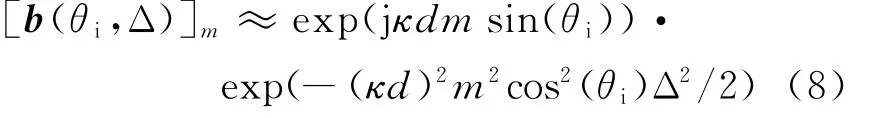
因此式(2)可以写作

式中，7表示Schur-Hadamard积，[h]m=exp(-(κd)2m2cos2(θi)Δ2/2)。

对于有限长接收数据，数据协方差矩阵的最大似然估计为

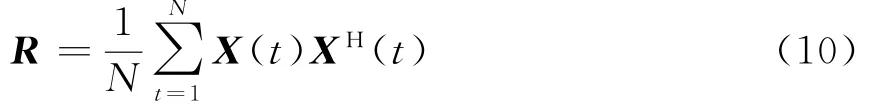
式中，N为快拍数，上标H表示共轭转置。

2 多维交替投影合成导向矢量最大似然算法

阵列接收的信号矢量中包括直达导向矢量和多径导向矢量，因此考虑将基于谱搜索的超分辨算法的导向矢量写为直达波和反射波两条路径的合成导向矢量形式，并将反射系数加入导向矢量，得到的合成导向矢量如下:

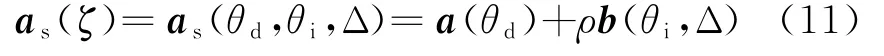
式中，ζ={θd，θi，Δ}。

利用合成导向矢量，通过ML或者MUSIC等超分辨算法在仰角域进行搜索，即可得到对应的目标仰角。

对于ML算法，首先，构成合成导向矢量的投影矩阵PML(ζ)，

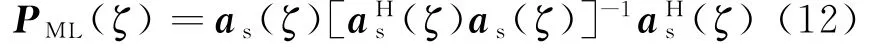
然后，得到三个参数的最大似然估计

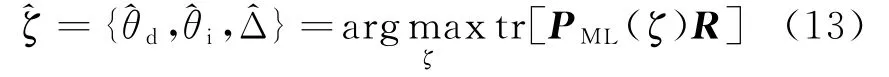
值得指出的是，合成导向矢量最大似然算法是一种模型匹配的方法，对于相关源无需进行解相关处理。

但是实际中，由于地面反射面复杂，无法知道多径信号角分布函数服从哪种分布以及角信号分布函数的分布参数。以高斯分布为例，可以看出其中的未知参数有三个:θd，θi和Δ。如果进行三维搜索来得到结果的话，运算量太大，这里提出一种较为简单的多维交替投影[9]算法。算法流程如下:

(1)假设多径信号为点信号源，使用文献[5]的算法计算出。将其作为随后迭代过程的初始值。

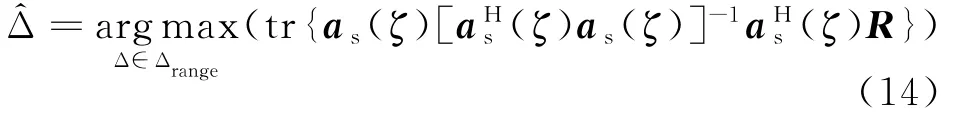
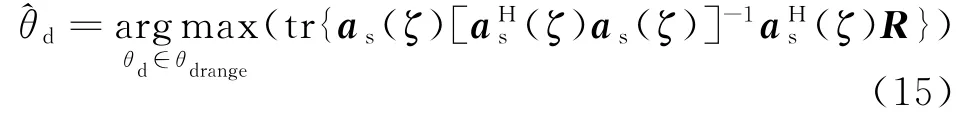
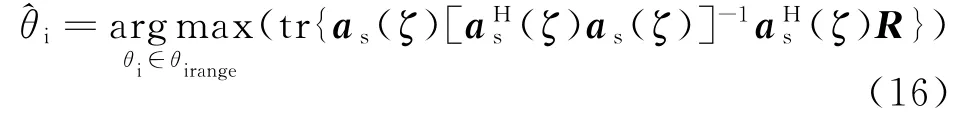
3 计算机仿真和实测数据处理

为了验证本文方法的有效性，仿真过程中，采用21阵元等间距垂直布阵的线性阵列天线，雷达架高为25m，载波频率为150MHz，天线间距半波长。将文献[5]算法与本文算法进行性能比较。单个目标，目标距天线阵中心的距离为200km，高度为5000m，直达波入射角为1.43°，多径信号为服从高斯分布的分布源，多径信号中心波达方向为-1.44°，Δ=1°，地面反射系数为-0.95，快拍数为20，阵元信噪比从-6dB变化至22dB。蒙特卡罗实验次数为200次。比较信噪比对算法估计精度的影响。

图3给出文献[5]算法与本文算法测角均方根误差随信噪比的变化。仿真结果表明，信噪比在-2 dB以下时，两种算法测角结果都较差，在-2 d B以上时，由于漫反射的影响，本文算法的测角均方根误差小于文献[5]算法的测角均方根误差。这说明漫反射是不可忽略的。

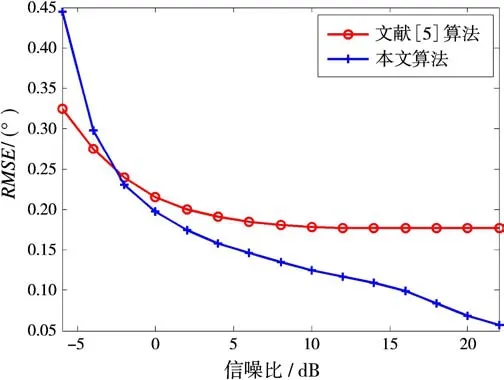
图3 信噪比变化时的性能曲线

为了验证本文方法在实际米波雷达测高中的性能，对架设在复杂阵地下的某米波雷达采集的实测数据进行处理，假设多径反射信号角分布函数服从高斯分布，分析测角和测高结果。

雷达架设在城市附近，地面反射面为城市，包括房屋、树林等不规则反射体。使用文献[5]算法与本文算法对实测数据进行处理。实测数据处理结果如图4(a)～(c)所示，其中图4(a)为目标飞行航迹图，箭头为目标运动方向，目标为切向向东飞行;图4(b)为仰角测量值随目标点迹的变化曲线;图4(c)为高度测量值随目标点迹的变化曲线;图4(d)为高度测量误差随目标点迹的变化曲线。

从实测数据处理结果中可见，当反射面较复杂时，仅文献[5]算法无法得到较好的结果，这是因为地面粗糙度不满足瑞利准则时，来自于粗糙面上的信号是镜面反射分量与漫反射分量之和，但漫反射占据较大的比重。相比较而言，本文算法能达到较高的测角和测高精度。以二次雷达结果为参考值，经统计，在整个航线上文献[5]算法的测角均方根误差和测高均方根误差分别为0.56°和1 315.6 m，本文算法的测角均方根误差和测高均方根误差分别为0.18°和320.2 m。

4 结束语

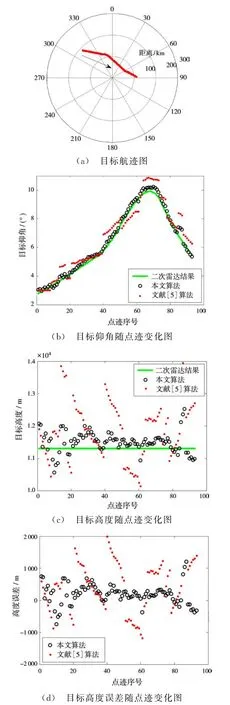
图4 城市反射面实测数据处理结果

米波雷达低仰角测高时受地面反射多径和宽接收波束的影响严重，测高效果不理想。尽管把多径认为是由地面上几何反射点这一个点所产生的这种近似分析方法常常能给出一些比较合理的结果，但是实际地面都有一定的粗糙度，所以只用一个镜像源来表示多径现象显然与实际不符合。为此本文建立了一种新的米波雷达低仰角信号模型，考虑漫反射的影响，将多径回波认为是分布源，使其更加符合实际多径回波的特征。提出利用多维交替投影和合成导向矢量最大似然算法进行低仰角测高。计算机仿真结果和实测数据处理结果证明本文算法能够有效地估计复杂多径环境下的目标仰角，相对于传统测高算法，能达到更高的测角和测高精度。应当指出的是，地面反射区的多径分布源模型很难确定，需要通过大量的实验来进行验证。

[1]LO T，LITVA J.Low-Angle Tracking Using a Multifrequency Sampled Aperture Radar[J].IEEE Trans on Aerospace and Electronic Systems，1991，27(5):797-805.

[2]LO T，LITVA J.Use of a Highly Deterministic Multipath Signal Model in Low-Angle Tracking[J].IEE Proceedings F Radar and Signal Processing，1991，138(2):163-171.

[3]刘张林，陈伯孝，杨雪亚，等.米波雷达最大似然超分辨测高技术研究[J].雷达科学与技术，2011，9(4):308-310.LIU Zhang-lin，CHEN Bo-xiao，YANG Xue-ya，et al.Research on Height Finding Technique Based on Maximum Likelihood Super Resolution in Meter-Wave Radar[J].Radar Science and Technology，2011，9(4):308-310.(in Chinese)

[4]杨雪亚.米波雷达阵列超分辨和测高方法研究[D].西安:西安电子科技大学，2011.

[5]ZHU Wei，CHEN Bai-xiao.Altitude Measurement Based on Terrain Matching in VHF Array Radar[J].Circuits，Systems，and Signal Processing 2013，32(2):647-662.

[6]张瑜，李玲玲.低角雷达跟踪时的多路径散射模型[J].电波科学学报，2004，19(1):83-86.ZHANG Yu，LI Ling-ling.Multipath Scatting Model of Low Angle Radar Tracking[J].Chinese Journal of Radio Science，2004，19(1):83-86.(in Chinese)

[7]HAN Y H，WANG J K，ZHAO Q，et al.Parameter Estimation Algorithm for Coherently Distributed Source[C]∥International Conference on Computer Design and Applications，[s.l.]:[s.n.]，2010:516-519.

[8]GRADSHTEYN I S，RYZHIK I M.Table of Integrals，Series，and Products(7th ed)[M].Orlando:Academic Press，2007.

[9]赵光辉，陈伯孝，董玫.基于交替投影的DOA估计方法及其在米波雷达中的应用[J].电子与信息学报，2008，30(1):224-227.ZHAO Guang-hui，CHEN Bai-xiao，DONG Mei.A New DOA Estimator Based on Alternating Projection and Its Application in VHF Radar[J].Journal of Electronics&Information Technology，2008，30(1):224-227.(in Chinese)