非单调税基税率曲线下的FL曲线探讨——兼论税基、税收最大相容存在的可能性
2014-03-20付广军
◆付广军 ◆刘 洋
笔者在关于FL 曲线①FL 曲线是指在三维空间坐标下税收与税率关系的曲线。参见付广军,刘 洋:《从拉弗曲线到FL 曲线的探讨》,《国家税务总局税收科学研究所研究报告》,2013 年第12 期。理论的探讨中讨论了税基税率曲线②税基税率曲线是指税基(国民产出)与税率关系的曲线。参见付广军,刘 洋:《关于拉弗曲线的理论探索和统计实证分析》,《国家税务总局税收科学研究所研究报告》,2013 年第5 期。的具体形式时,假定不存在外部性和公共品,即认为税率为零时,生产活动能够正常有序的进行,没有任何税负,税基取得最大值,这保证了税基税率曲线的单调性,使得分析过程相对简单。然而更为贴近实际的情况是,当税率为零时,政府不能提供任何公共服务以及监管措施,而公共品的非排他性和某些经济活动的外部不经济会导致生产活动混乱,造成经济效率的损失,税基(国民产出)因此不会达到最大化。
一、非单调的税基税率曲线
在确定税基税率曲线的形式时,考虑外部性和公共品。税率为零时,税基并不能取得最大值。当税率处于某一水平(可能是一个相对低的税率水平)时,由于政府提供了公共服务以及监管措施,使得经济效率处于较高水平,税基取得最大值。
此时的税基税率曲线就是非单调的。假设税基税率曲线具有如下的函数形式:


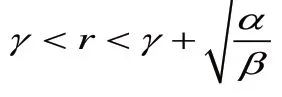
二、非单调税基税率曲线对应的FL 曲线
由式(1)推导出税收税率曲线的函数形式为:


式(4)对r 求导,得:

表1 描述了税基税率曲线和税收税率曲线的大致图形特征,示意图见图1、图2。

表1 非单调税基税率曲线及其对应税收税率曲线的形态描述

税收税率曲线一阶导 >0 >0 >0 >0 >0 >0 0 <0 <0二阶导 >0 >0 0 <0 <0 <0 <0 <0 <0形态/取值 单调上升(加速) 凹凸性拐 点 单调上升(减速) 极大值 单调下降(加速)
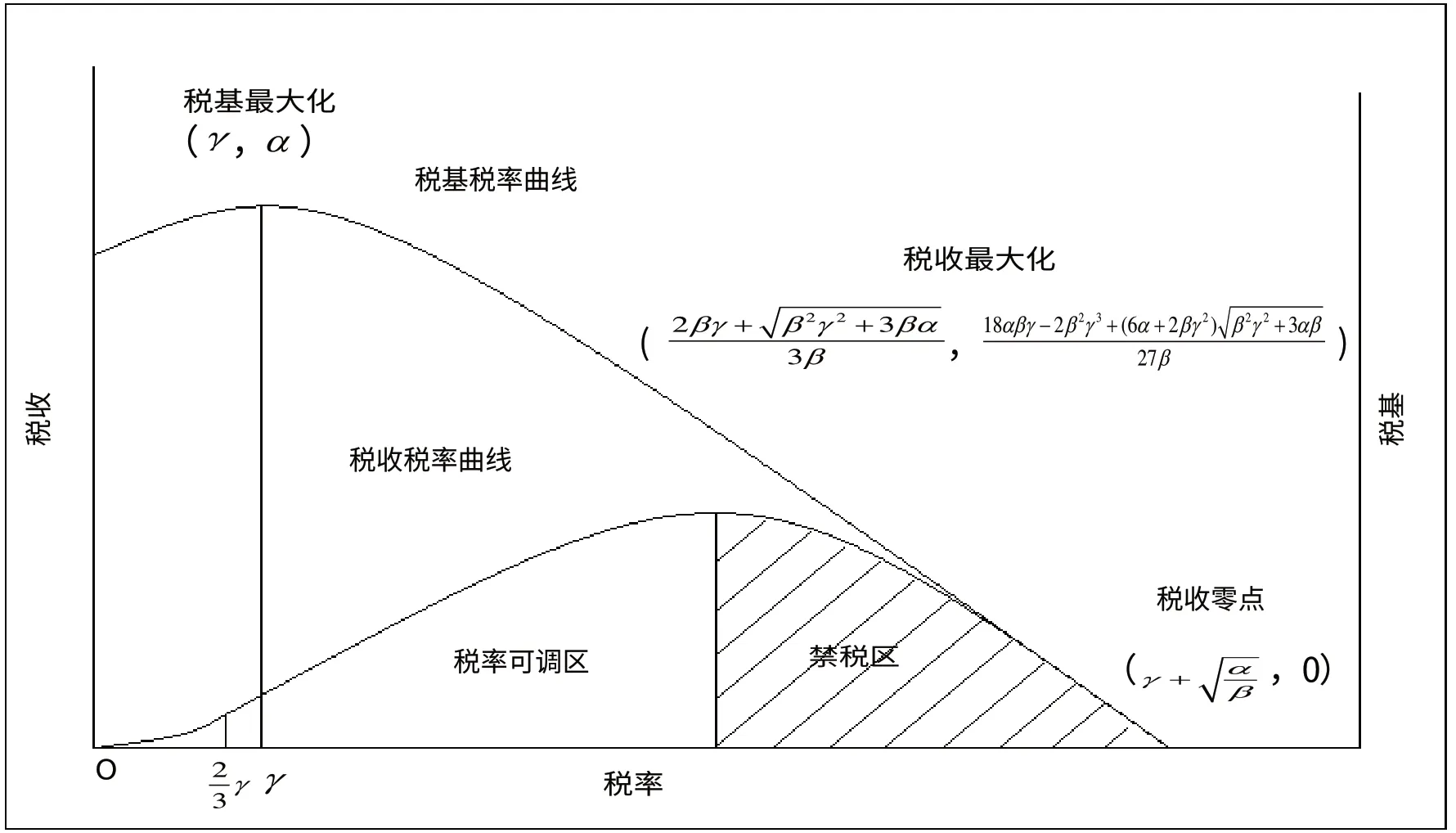
图1 非单调税基税率曲线及其对应的税收税率曲线
图2 为此时三维空间坐标下的FL 曲线示意图。

图2 非单调税基税率曲线对应的FL 曲线
三、税基税率曲线单调条件下税基最大化税率与税收最大化税率的相对位置
在讨论单调的税基税率曲线时,税基最大化税率为零,而税收最大化税率随税基税率曲线的不同形式而改变。不同税基税率曲线(单调)条件下,税基最大化税率与税收最大化税率取值见表2。
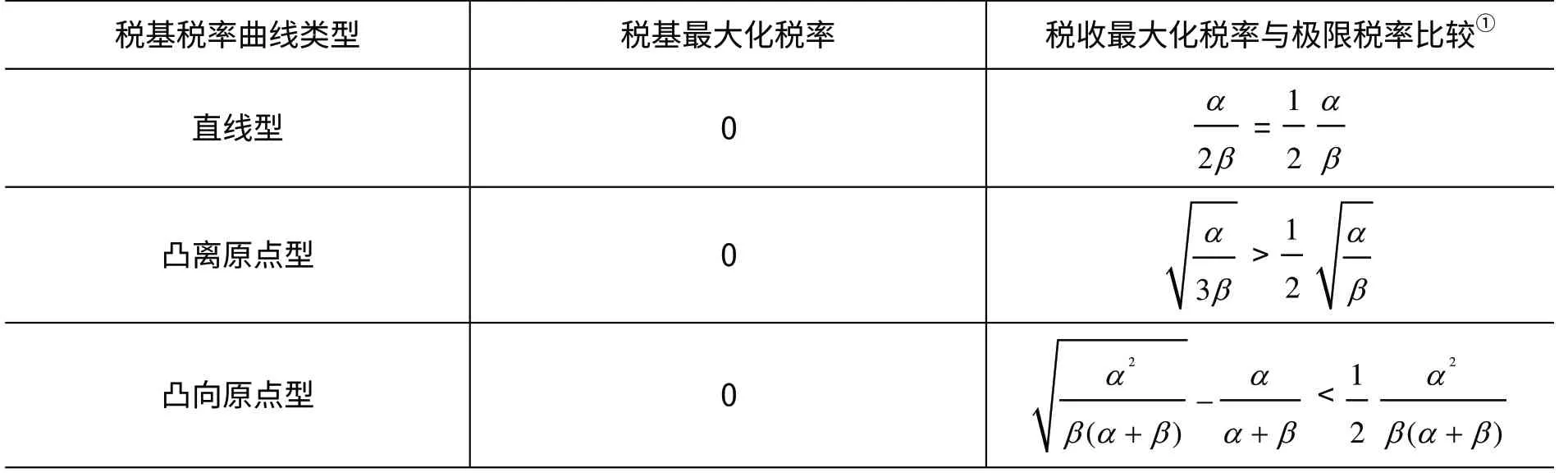
表2 税基税率曲线单调递减条件下税基最大化税率与税收最大化税率取值表
从表2 中可以看出,当税基税率曲线凸离原点时,税收最大化税率距离税基最大化税率较远;②此处的“远”、“近”并不是绝对数值的远近,而是税收最大化税率在可取的税率范围内的百分比的远近。当税基税率曲线凸向原点时,税收最大化税率距离税基最大化税率较近。因此,如果设想税基税率曲线成L 形状,此时的税基税率曲线为凸向原点,税率为一无限趋近于零的数值时,税收可能达到最大值,其对应的税收最大化税率(无限趋近于零的一个税率数值)无限接近于税基最大化税率(零);如果设想税基税率曲线成倒L 形状,此时的税基税率曲线为凸离原点,税率为一无限趋近于极限税率的数值时,税收可能达到最大值,其对应的税收最大化税率(无限趋近于极限税率的一个税率数值)距离税基最大化税率(零)最远。
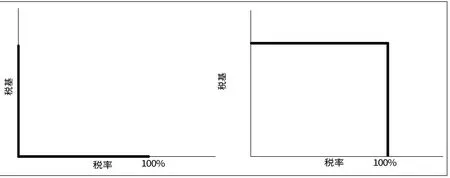
图3 两种极限情况下的税基税率曲线
如图3 所示,成L 形状的税基税率曲线表明,对于全部经济活动参与者而言,任何对于其劳动收入所得的征税行为都会使单位时间内劳动收入的效用小于单位时间闲暇的效用,使其放弃劳动而选择闲暇。而成倒L 形状的税基税率曲线表明,对于全部经济活动参与者而言,只要其劳动收入仍有部分归属于个人支配,那么单位时间内劳动收入的效用将始终大于单位时间闲暇的效用,所以直到税率达到100%之前,全部经济活动参与者都会选择劳动。
四、税基税率曲线非单调条件下税基、税收最大相容
为方便讨论,笔者再次将税基税率曲线、税收税率曲线的函数形式列出:

。

然而,笔者认为在某些特定的经济条件与社会心理条件下,税收、税基的最大相容在数学形式上可以存在,在实际的经济生活中也可能具有非常接近的状态。
基于本文在税基税率曲线单调条件下税基最大化税率与税收最大化税率的相对位置的论述,笔者现构造如下税基税率曲线函数:
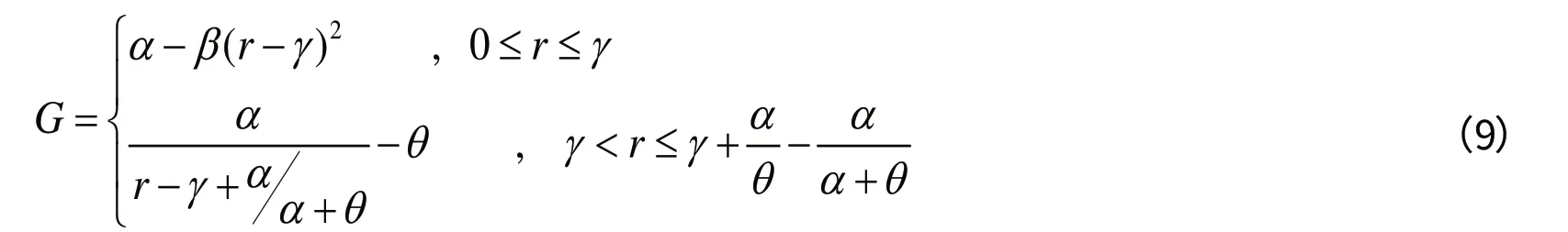
由式(9)推导出对应的税收税率曲线函数:
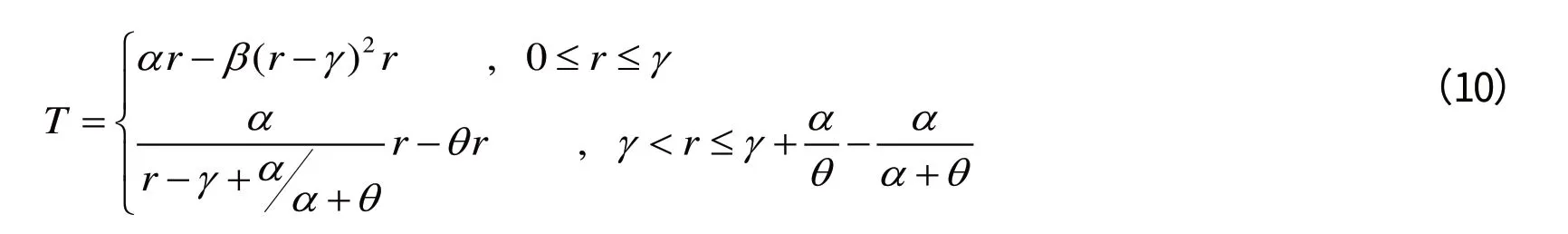
参数约束同式(9)。


。可以发现,在这种情况下,分段税基税率曲线函数与普通的非单调税基税率曲线函数以及两者分别对应的税收税率曲线函数并无本质上的区别。税基、税收此时依旧不相容,示意图如图4。

图4 税基、税收最大不相容
三维空间坐标FL 曲线下的税基、税收最大不相容如图5。
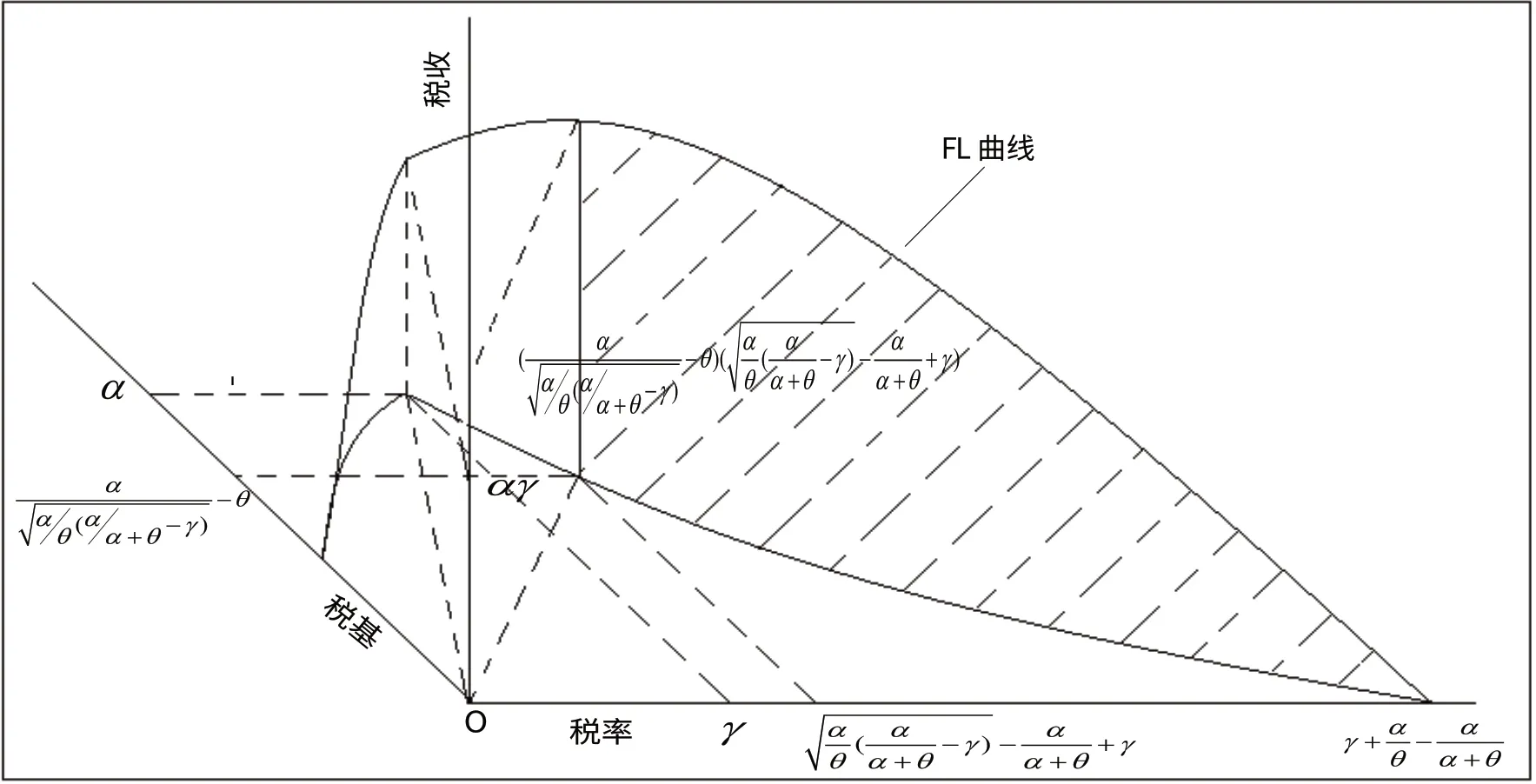
图5 FL 曲线下的税基、税收最大不相容
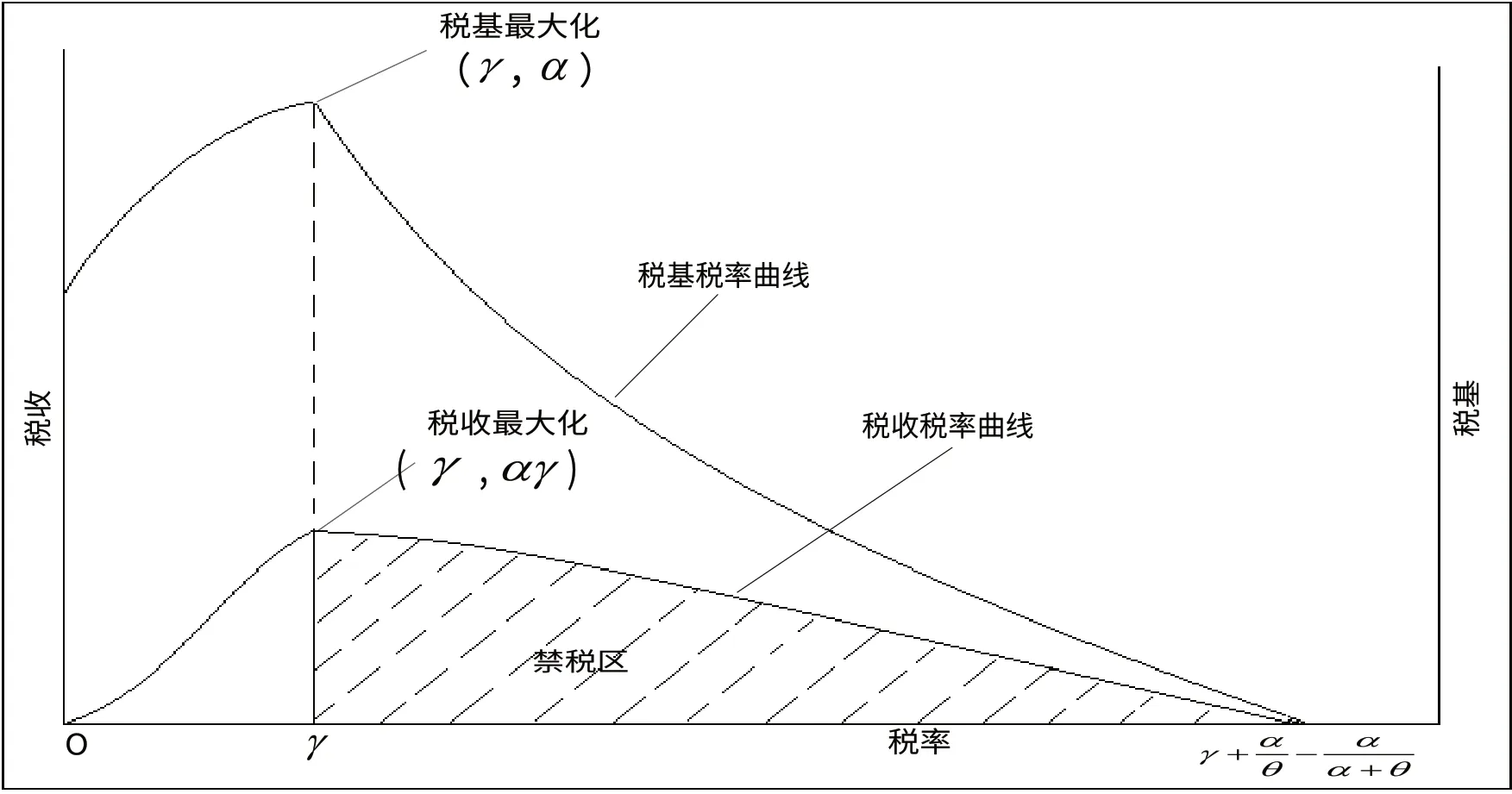
图6 税基税收最大相容
三维空间坐标FL 曲线下的税基、税收最大相容如图7。
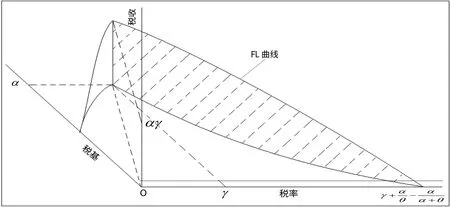
图7 FL 曲线下的税基税收最大相容
税基、税收最大相容的证明,从数学角度证明了使税基、税收同时达到最大的最优税率的存在①笔者认为,使税基(国民产出)、税收(政府收入)同时达到最大化的税率为真正的最优税率。。在该最优税率点下,国民经济取得最大化,政府税收收入也取得最大化,这是任何一个国家或者政府都期望处于的经济发展状态(单就政府税收和经济总量而言)。
现将分段税基税率曲线在两种情况下的税基最大取值和税收最大取值及其取得条件总结成表3。

表3 分段税基税率曲线在两种情况下的税基最大取值和税收最大取值
分段税基税率曲线的构造有一定的社会经济发展规律,曲线的形态取决于两个因素:政府提供的基础设施建设和规范的市场秩序对经济发展的促进作用;单位时间劳动收入和闲暇的相对效用。
当政府开始对一个无秩序市场开始进行管理时,政府提供的基础设施建设和规范的市场秩序对经济发展的促进作用较为显著。虽然经济活动参与者的劳动收入被占有了一部分,但是由于此时经济发展较快,市场条件良好,对绝大多数经济活动参与者而言,单位时间劳动收入的效用大于闲暇的效用,较少人会去选择闲暇,经济总量会不断上升;然而政府提供的基础设施建设和规范的市场秩序对经济发展的促进作用在超过某一限定后,其经济效率必然下降,此时政府通过高税率获得了更多的税收收入,但是其所能带来的经济促进作用却极为有限,有些情况下甚至由于政府投资的低效率反而降低了经济发展速度,同时经济活动参与者由于高税负和较慢的经济发展速度,更多的人会选择闲暇,经济总量不断减少。
因此,可以预见,分段税基税率曲线在现实的社会经济发展当中也具有存在的可能性,税基、税收的最大相容可能会在某个社会经济发展状态中出现。
五、总结
事实上,经济总量(税基)与税率之间的关系并没有确定的函数形式可以来描述,随着经济发展水平、经济增长结构、经济增长动力、技术进步的变化,在特定的时期,经济总量与税率之间的具体函数形式会有显著的不同。笔者从最简单情况的非单调税基税率曲线以及对应FL 曲线的分析,再次证明了简单条件下的最大不相容原理,之后又创新性地构造了分段形式的非单调税基税率曲线,详细阐述了分段函数在不同的参数约束条件下税基最大和税收最大的取值和取得条件,最终证明了在数学形式上可以通过适当的参数约束使得税基最大和税收最大能够相容,求出了最大相容税率(最优税率)值的解析解,并且给出了税基、税收最大相容在实际社会经济发展中存在的原理性描述。
[1]周 伟,武康平.个人所得税、政府转移支付与个体行为激励—基于拉弗曲线的统一讨论[J].南开经济研究,2011,(5).
[2]王书瑶.财政支出最大与国民产出最大不相容原理[J].数量经济技术经济研究,1988,(10).
[3]付广军,刘 洋.关于拉弗曲线的理论探索和统计实证分析[R].国家税务总局税收科学研究所研究报告,2013,(5).
[4]付广军,刘 洋.从拉弗曲线到FL 曲线的探讨[R].国家税务总局税收科学研究所研究报告,2013,(12).
