一类超混沌Liu系统动力学分析

张 莉， 李耀伟， 俞建宁， 杨 敏

(1. 兰州工业学院 基础学科部, 甘肃 兰州 730050; 2.兰州交通大学 数理学院， 甘肃 兰州 730070)

混沌是一种在确定性系统中出现的类似随机而无规则的动力学行为，近年来，它已成为非线性科学研究领域的热点问题.混沌系统具有内随机性、连续宽谱和对初始值极端敏感等特点，因此具有极其广阔的应用范围．Rössler在1979年首次提出了一个超混沌系统[1]，并且证明了超混沌系统具有两个正的Lyapunov指数．由于超混沌系统具有一个以上的正Lyapunov指数，所以其动力学行为和周期解可以扩展到更多的方向[2-3]，与混沌系统相比超混沌系统具有更丰富的动力学特性，更大的随机性以及不可预测性[4-5].已有的超混沌系统的研究大多集中在混沌的实现机制以及同步方面，而关于高维系统或超混沌系统的Hopf分岔分析研究很少.2006年，王发强等在Liu系统加入一个控制器产生了四维的混沌系统[6]，通过计算李雅普诺芙指数和电路实验证明该系统是超混沌的2个正的Lyapunov指数，称为超混沌Liu系统[7].关于该超混沌系统的Hopf分岔，目前还没有文献进行过研究，本文研究该系统的动力学特性以及Hopf分岔行为，得出系统发生Hopf时系统参数应当满足的条件，并求得系统发生Hopf分岔时极限环的方向与稳定性，最后运用数值仿真对理论分析进行验证.

1 基本动力学行为

超混沌Liu系统的非线性动力学模型为

(1)

该系统是在Liu系统的基础上添加一个控制项w得到的，当a=10,b=40,c=2.5,h=4,k=1,d=10.6时系统处于超混沌状态，其Lyapunov与分形维数分别为LE1=1.414 9，LE2=0.126，LE3=0，LE4=-13.767,DL=3.927,系统有两个正的Lyapunov指数，所以系统存在一个超混沌吸引子，其吸引子如图1(a)所示，系统(1)的时间响应图、Lyapunov指数谱图、Poincare截面图如图1(b)、图1(c)、图1(d)所示.

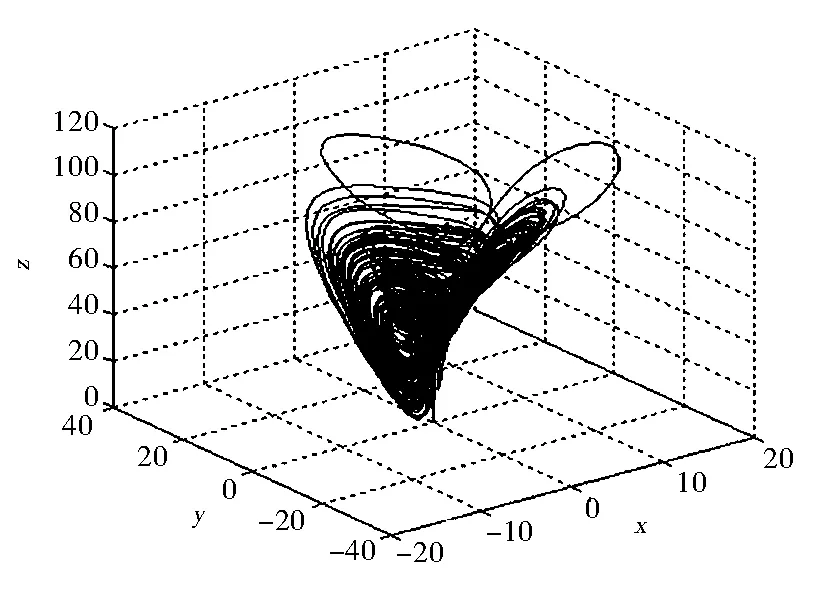
(a) 三维空间吸引子图

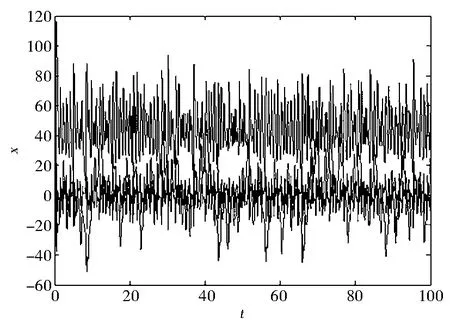
(b) 系统时间响应图

(c) Lyapunov指数谱图

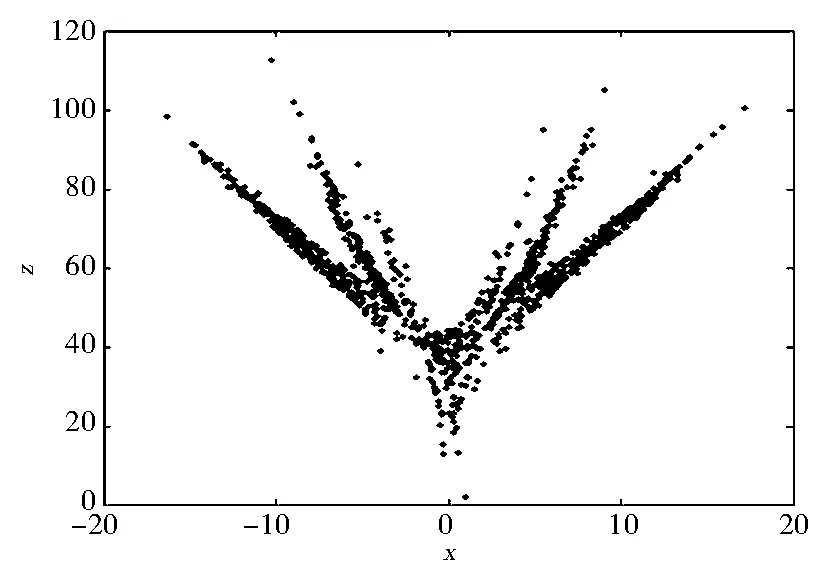
(d) Poincaré截面图

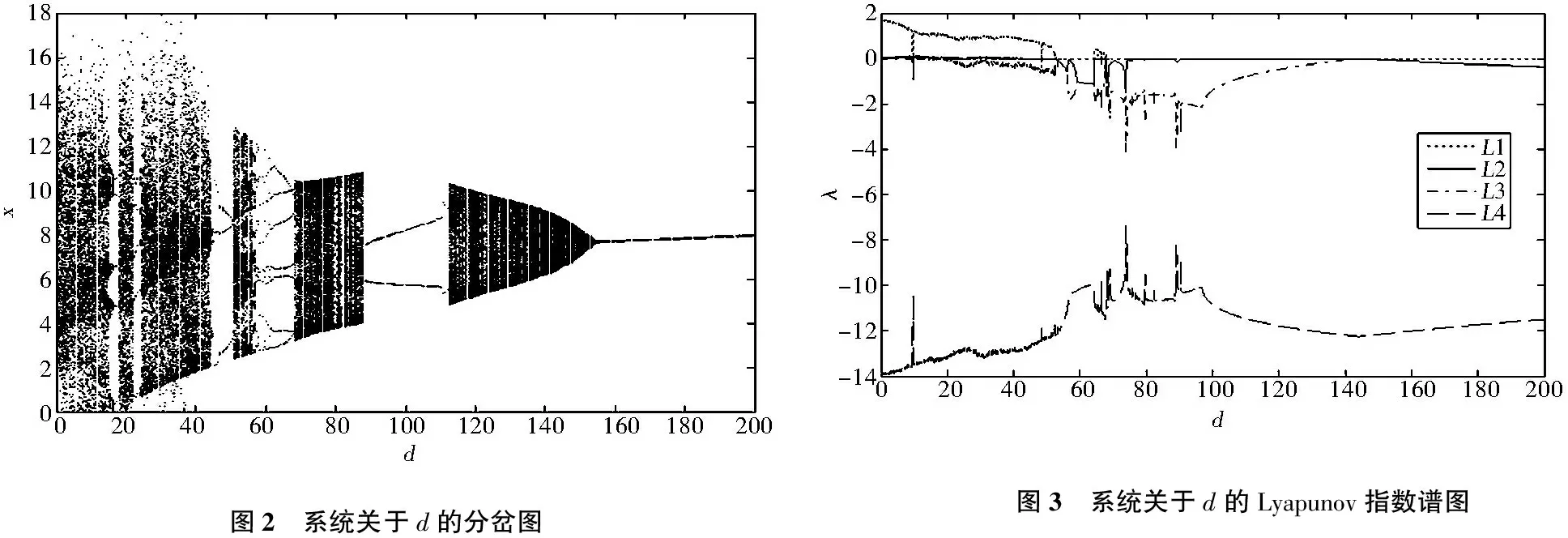
应用Matlab数值仿真，固定a=10，b=40,k=1,c=2.5,h=4,以d作为变量可以得到系统关于d的分岔图和Lyapunov指数谱图，分别如图2和图3所示.

从图2的分岔图和图3的Lyapunov指数谱图中可以观察到，随着d取值区间的不同系统出现了超混沌、混沌、周期、拟周期等不同的动力学行为，图4给出了这4种运动状态下的x1-x4平面相图．

2 平衡点稳定性与Hopf分岔分析

令系统(1)方程的右端等于零，即

(2)

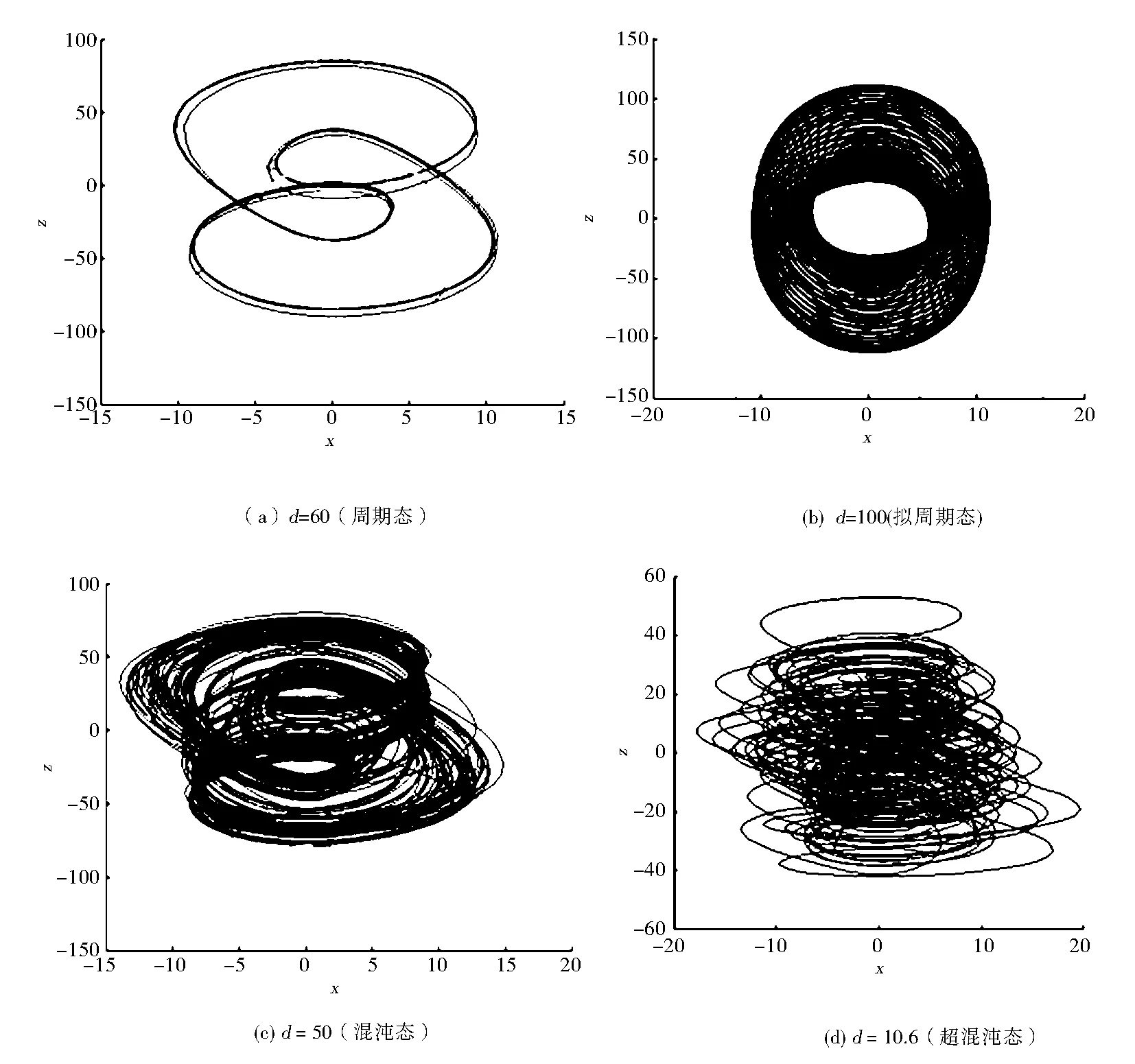
图4 4种运动状态下系统x1-x4平面相图

可以得到系统的唯一平衡点(0,0,0,0)，方程(2)的Jacobi矩阵为

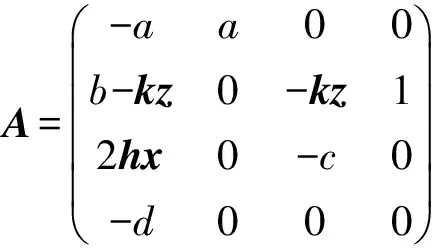
(3)

令|λI-A|=0，方程(2)在(0,0,0,0)对应的Jacobi特征多项式为

λ4+(a+c)λ3+(ac-ab)λ2+

(ad-abc)λ+acd=0

(4)

由Routh-Hurwitz判据可知方程(4)的一切根的实部为负数的必要且充分条件是

(5)

从式(5)中可以解得

(6)

命题1当条件(6)满足时系统(1)是渐近稳定的．

命题2当d=-ab,a>b,-ab>0时系统在平衡点O(0,0,0,0)处发生Hopf分岔．

证明特征多项式(4)可化为如下的等价形式：

(λ+c)(λ3+aλ2-abλ+ad)=0

(7)

则特征多项式有一特征根为λ1=-c，考虑多项式

λ3+aλ2-abλ+ad=0

(8)

假设式(8)有一对共轭的纯虚根λ2,3=±ωi(ω>0)，将λ2,3=±ωi带入(8)可得

-ω3i-aω2-abωi+ad=0

(9)

(9)式为零的充要条件是实部与虚部都为零，分离实部与虚部有

(10)

从(10)式可以解得

(11)

经计算可得

(12)

3 极限环的方向和稳定性

这里运用范式理论[8]研究系统(1)发生Hopf分岔所分支出来的极限环的方向稳定性.通过计算，可以求得满足Av1=iω0v1,Av3=-cv3,Av4=-av4的特征向量

对系统(1)定义如下矩阵

P=(Reν1,-Imν1,ν3,v4)=

和变换

(x1,y1,z1,u1)T=P(x2,y2,z2,u2)T

从而有

其中

F1(x2,y2,z2,u2)=

F2(x2,y2,z2,u2)=

应用Hassard等在文献[9]中提出的方法，进而有

通过解以下方程

Dw11=-h11,(D-2iω0I)w20=-h20

可得

其中

基于上面的分析和计算可得

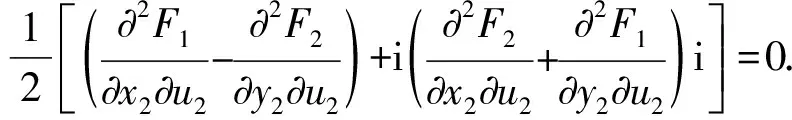
因此，可以得到以下的表达式

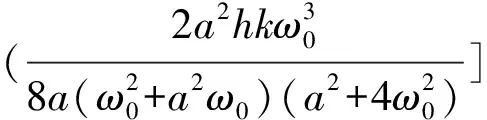
μ2决定Hopf分岔的方向：如果μ2>0(μ<0)，则Hopf分岔是亚临界的(超临界的).β2决定极限环的稳定性：β2<0(β2>0)，则极限环是稳定的(不稳定的).τ2决定极限环的周期：τ2>0(τ2<0)时，周期是递增的(递减的).设a<0,b>0，则有Re(x′(d0))>0，因此，系统(1)发生Hopf分岔.

4 数值仿真

为了验证以上的理论分析，我们选取一组参数:a=2,b=-2，可以得到Hopf的临界值d=d0=4.系统在发生Hopf前后的系统相图如图5～图8所示．

从图5中可以看出当d=4系统出现极限环，这与系统发生Hopf分岔时在分岔点出会出现极限环的理论相一致，所以系统在d=4处发生了Hopf分岔，证明了理论分析的正确性．

5 结束语

本文分析了超混沌Liu系统的基本动力学特性并运用数值仿真的方法进行了验证，分析了系统的分岔特性，得出系统发生Hopf分岔时应当满足的参数条件．选取适当的参数，可以证明当分岔参数超过某一临界值时系统会发生Hopf分岔，并运用范式的方法求得系统发生Hopf分岔时极限环的方向和稳定性．数值仿真验证了理论分析的正确性．尽管本文研究的系统较简单，但它有着十分丰富的动力学特性，该系统混沌吸引子的形成机理及其拓扑结构还需进一步分析.因此，对系统的进一步研究仍然具有重要意义．

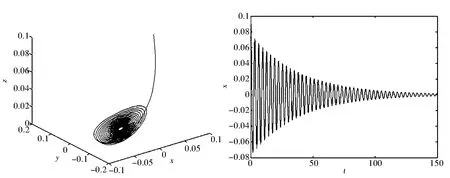
图5 d=3.8时系统的相图与时间响应图

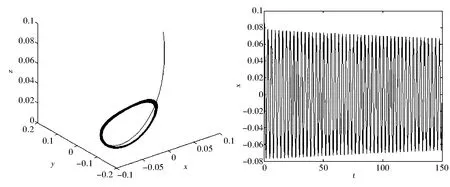
图6 d=4时系统的相图与时间响应图

图7 d=4.2时系统的相图与时间响应图

图8 d=4.5时系统的相图与时间响应图

[1]RösslerOE.Anequationforhyperchaos[J].PhysLettA, 1979, 71(2):155-157.

[2]WuXJ,WangH,LuHT.Modifiedgeneralizedprojectivesynchronizationofanewfractional-orderhyperchaoticsystemanditsapplicationtosecurecommunication[J].NonlinearAnalysis:RealWorldApplication，2012.13(3):1 441-1 450.

[3]LiuYJ.Circuitimplementationandfinite-timesynchronizationofthe4DRabinovichhyperchaoticsystem[J].NonlinearDynamics,2012, 67(1):89-96 .

[4]PangSQ,LiuYJ.AnewhyperchaoticsystemfromtheLsystemanditscontrol[J].JournalofComputationalandAppliedMathematics，2011,235(8):2 775-2 789.

[5]NiuYJ,WangXY,WangMJ,et al.Anewhyperchaoticsystemanditscircuitimplementation[J].CommunicationsinNonlinearScienceandNumericalSimulation,2010, 15(11):3 518-3 524 .

[6]WangFQ,LiuCX.HyperchaosevolvedfromtheLiuchaoticsystem[J].ChinesePhys.2006, 15(5):963-968.

[7]WangXY,WangMJ.Ahyperchaosgeneratedfromlorenzsystem[J].PhysicaA:StatisticalMechanicsanditsApplications2008,387(14): 3 751 3 758.

[8]ZhuangKJ.Hopfbifurcationforanewchaoticsystem[J].InternationalJournalofComputationalandMathematicalSciences,2010(4): 358-361.

[9]HassardBD,KazarinoffNDWanYH.TheoryandapplicationsofHopfbifurcation[M]. 1sted.Cambridge:CambridgeUniversityPress， 1911.