模拟盒参数对汽液体系模拟过程的影响

何 川，李少华，时 雯

（重庆大学动力工程学院教育部低品位能源利用技术及系统重点实验室，重庆400044）

1 引 言

关于汽液界面的研究一直是人们关注的热门课题，不仅在实际工程领域有着广泛应用，而且也是基础理论研究的重要方面.Adamason［1］指出，界面层区域是一种介于气相区与液相区的过渡态区域.界面层很薄，通常只有几到几十个分子的厚度，随时间和空间变化而不断涨落起伏，现有的实验技术在汽液界面的研究上还存在一些困难.

分子动力学模拟是近年来发展起来的数值计算方法，一方面可以从微观角度模拟分子行为，另一方面也可以通过大量统计计算获得宏观热力学参数，因此变成了汽液界面研究中的有效方法.Chapela［2］等人首次提出了将汽液平衡体系分为气相区、液相区和气-液界面区三部分的模拟体系.基于这种方法，国内外学者做了很多相关研究：Holcomb［3］等人的研究表明，汽液界面的密度、张量等热力学参数是连续变化的，可依据密度变化定义体系中的汽相区、过渡区和液相区；Mecke［4］等人研究了截断半径对界面特性的影响，提出LRC方法；刘朝、曾丹苓［5］进一步研究了截断半径和分子数对界面张力的影响情况.

通过分析文献［3］～［5］以及笔者的模拟结果，发现这些传统的模拟方法与实验测量相比存在较为明显的偏差，过去对于分子模拟方法的改进研究大多针对势函数截断半径及模拟分子数，往往忽略了模拟盒参数的影响.通过增加分子数量，延长截断半径的确可以提高计算结果的准确性，但是随之而来的则是计算时间呈几倍乃至十几倍的增加，计算效率大大降低，优化模拟的代价很高昂.为了提高模拟结果的准确性，同时也确保不增加模拟时间及计算机压力，本文从模拟盒参数的角度入手，对饱和汽液共存体系的分子行为进行模拟，研究系统切片数、汽相空间尺寸、液膜厚度以及时间步长等模拟盒因素对结果的影响，为进一步改进和优化分子动力学模拟方法提供依据.

2 模拟方法

模拟对象为常用的Lennard-Jones流体氩，其势能函数形式为：

其中，σ=3.405×10-10m，ε=1.67×10-21J.

由于受到计算能力限制，通常选取较少的分子数目进行模拟，又为避免因分子太少引起尺度效应，参考文献［5］，选取1000作为合适的模拟分子数.模拟系综为NVT 正则系综，即系统的分子数n、容积V 和温度T 保持不变.采用直角坐标系，系统在x、y、z方向的尺寸分别为Lx、Ly、Lz.

初始时刻的分子为饱和液相分子，速率呈Maxwell分布，以正方体FCC 结构均匀密集分布在系统中央，形成一块扁平的薄液膜层，液膜表面垂直于z方向，如图1所示.液膜质心在原点（0，0，0）处，为防止系统出现宏观漂移，模拟中需要不断调整液膜质心为系统的中心位置.势能截断半径为3.5σ，为提高计算效率，采用Verlet-List搜寻法，搜寻半径为4σ.模拟体系在xyz 方向均采用周期性边界条件，不考虑外势场（如重力场）的作用.为进一步提高效率和节约内存，本文采用动态存储方法，合理的分配和释放包含分子信息的内存空间.

采用leapfrog差分算法［6］求解粒子的运动方程，在计算过程中，需要不断对粒子速度进行修正，以确保系统温度维持在设定值.

图1 模拟系统示意图Fig.1 Simulation system diagram

由于从纯饱和液态变化到汽液共存态需要较长时间，为达到汽液平衡状态，每一次模拟长度规定为1×105分子动力学步.当系统处于平衡时，不仅系统的能量和气相分子数保持不变，而且密度和压力张量等分布随时间也不产生变化.平衡后的统计长度为1×105分子动力学步，每隔100步统计一次.将系统沿z方向平行于x-y 平面平均分为NS个切片进行统计，温度、压力张量以及表面张力的统计公式如下［7，8，9］：

其中，ρ（k）为第k 切片的分子数密度，T（k）为第k切片的温度，pN（k）、pT（k）为第k切片的法向应力和切向应力，nk为第k 切片内的分子数，vi为分子i的速度，γ（k）为第k 切片的局部张力，γ 为液膜的表面张力，xij、yij、zij、rij分别为分子i 和j 之间在x、y、z方向及空间r 的距离，Vsl=LxLyLz／NS为一个切片的体积，U＇为势函数对r 的导数，＜＞为正则系综统计平均值.统计时，如果i和j 两个分子都在第k 切片内，则将其值全部计入，如只有其中一个分子位于第k切片内，则计入值的一半.

在模拟过程中，为确保体系各物理量之间的数量级较为接近，减小模拟过程中出现的截断误差，将所用到的各物理量进行无量纲化.无量纲化处理后的无因次参数如下：

长度L＊=L／σ；时间t＊=t／（σ（m／ε）1／2）；温度T＊=KBT／ε；表面张力γ＊=γσ2／ε；密度ρ＊=ρσ3／m；压力张量P＊=Pσ3／ε；作用势U＊=U／ε

3 结果与分析

2.1 传统模拟结果

针对温度为84K～140K、具有相同分子数的汽液共存系统进行了传统方法的分子动力学模拟.其他参数设置如下：液膜厚度为16分子数，汽相空间为50σ，系统切片数为100，时间步长为5×10-15s，具体参见表1.

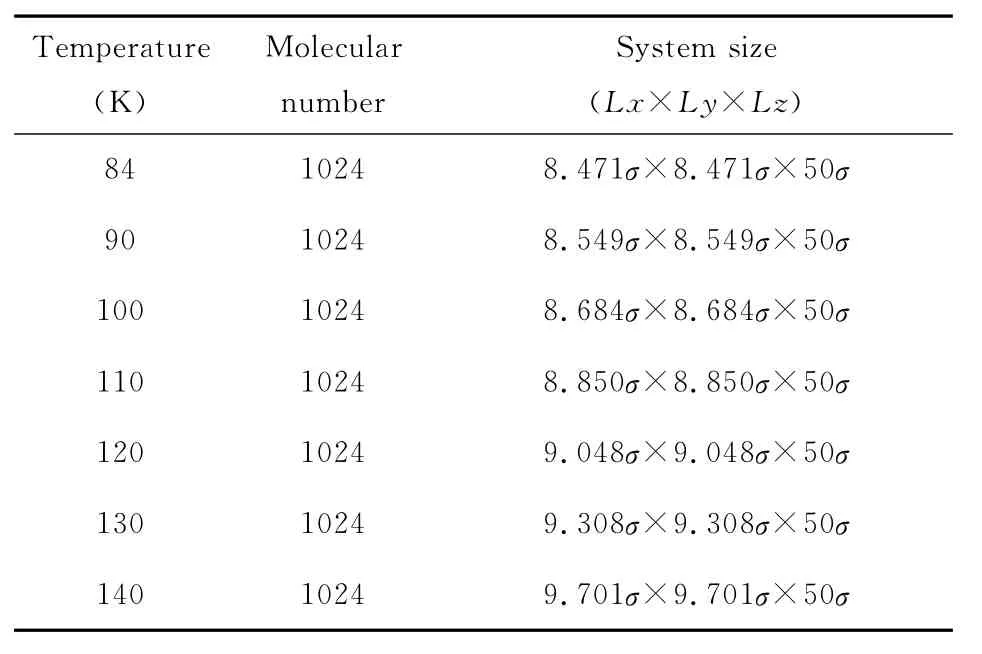
表1 分子动力学模拟的参数Table 1 Parameters of molecular dynamics simulation

图2给出了不同温度下的系统的密度分布情况，图中无量纲尺寸z＊=z／σ.可以看出，随着温度的升高，汽液过渡区厚度增加，汽相密度相应增大，液相密度随之降低.当温度达到140K 时，汽相与液相密度竟然已经大体相等，很难严格区分气态分子与液态分子，这是由于温度已经接近氩的临界温度（Tc=150K），处于该温度下的饱和液和饱和气具有相同的临界状态［10］.

图3给出了不同温度下的系统的表面张力变化情况，随着温度的提高，表面张力逐渐降低.通过与文献［11］实验测量值的比较，存在较为明显的偏差，模拟结果不太理想.因此有必要对其进行优化改进，既要提高结果的准确性和可靠性，也要确保模拟的高效与时间的节约.

图2 不同温度下系统的密度分布，（z＊=z／σ）Fig.2 Density distribution of the system with temperature T，（z＊=z／σ）

图3 不同温度下系统的表面张力变化Fig.3 Surface tension changes with temperature T

3.2 模拟盒参数影响情况

在传统分子动力学模拟的基础上，笔者从模拟盒参数的角度入手，对饱和汽液体系进行模拟，研究当系统温度为100K 时，系统切片数、汽相空间尺寸、液膜厚度以及时间步长等模拟盒因素对模拟计算结果的影响.

图4给出的是不同切片数下表面张力的变化情况.可以看出，切片数NS从50增加到200，系统的表面张力基本不变化，这是由于式（2）～（7）均为全遍历性的统计方式，其计算结果与切片数无关.切片数量仅仅会影响局部参数（如汽液界面密度、局部张力等）的精确性.

图4 表面张力γ＊随切片数Ns的变化情况Fig.4 Surface tensionγ＊ changes with the number of slices Ns

图5、图6给出的是汽液界面密度以及系统表面张力随体系z轴尺寸的变化情况，图中的无量纲尺寸Lz＊=Lz／σ.Lz 较小时，模拟体系的汽相空间较小，无法体现周期性无限空间的特点，分子运动将受到空间大小的限制；Lz 过大则会导致汽相密度增加，用于统计界面张量的液相分子数相应减少，造成统计误差.图6的结果表明了，在本文模拟的工况中，当Lz＊为60时，表面张力的计算结果为0.647，与文献［11］中提供的实验值0.654十分接近，误差仅为1.1%.

图5 不同Lz＊时界面密度的变化情况，（Lz＊=Lz／σ）Fig.5 Interface density changes with Lz＊，（Lz＊=Lz／σ）

图6 表面张力γ＊随Lz＊的变化情况，（Lz＊=Lz／σ）Fig.6 Surface tensionγ＊changes with Lz＊，（Lz＊=Lz／σ）

图7和图8给出的是相似分子数下，初始时刻不同的液膜厚度对平衡后表面张力及液相密度的影响情况.实际情况中的液膜比较厚，两侧界面的分子不会互相干扰，而模拟计算中，为节约计算时间，液膜通常设置的比较薄，只有几到十几个分子厚度，这就会导致液膜两侧界面分子相互作用，产生较大的误差.从图中可以看出，表面张力会随着液膜厚度的增加而接近实验值，规定无量纲厚度d＊=d／σ，当d＊达到13以后，液相密度趋于稳定，两侧界面分子将不会相互影响，与实际情况相符，满足模拟要求.

图9、图10给出了当系统处于平衡状态后改变分子动力学步长Δt会对液相密度及张力造成的影响.从图中可以看出，改变步长不会影响到平衡后的体系密度，但会对表面张力的计算影响较明显.当步长选择为11fs（10-15s）时，结果较为接近实验值.

图7 表面张力γ＊随d＊的变化情况，（d＊=d／σ）Fig.7 Surface tensionγ＊changes with d＊，（d＊=d／σ）

图8 液相密度随d＊的变化情况，（d＊=d／σ）Fig.8 Liquid density changes with d＊，（d＊=d／σ）

图9 液相密度随步长的变化情况Fig.9 Liquid density changes with time step

图10 表面张力γ＊随步长的变化情况Fig.10 Surface tensionγ＊changes with time step

4 结 论

采用分子动力学方法模拟饱和汽液共存体系中汽液界面现象，得到了温度为100K 时，系统切片数、汽相空间尺寸、液膜厚度以及时间步长等模拟盒因素对结果的影响，结果表明：

（1）传统的分子动力学模拟方法忽略了模拟盒参数的设置，计算结果与实验测量值相比存在较为明显的差距.

（2）系统切片数不会影响表面张力以及两相密度的模拟结果，仅仅会对局部参数的精确性产生一定程度的影响.

（3）汽相空间尺寸会对模拟过程产生较大的影响.无量纲尺寸Lz＊为60时，表面张力的模拟结果与实验值吻合较好，误差仅为1.1%.

（4）液膜厚度关系到两侧界面分子是否会相互干扰.当厚度达到13，液相密度趋于稳定，两侧界面分子将不会相互影响.

（5）分子动力学步长不会影响平衡后的体系密度，但对表面张力的计算影响较明显，当步长为11 fs，计算结果理想.

.

［1］ Adamson A W.Physical chemistry of surface［M］.New York：John Wiley ＆Sons，1982.

［2］ Chapela G A，Saville G，Thompson S M，et al.Computer simulation of a gas-liquid surface ［J］.Journal of the Chemical Society，Faraday Transactions，1977，73（2）：1133.

［3］ Holcomb C D，Clancy P，Zollweg J A.A critical study of the simulation of the liquid-vapor interface of a Lennard-Jones fluid［J］.Mole.Phys.，1993，78（2）：437.

［4］ Mecke M，Winkelmann J，Fischer J.Molecular dynamics simulation of the liquid-vapor interface：The Lennard-Jones fluid［J］.J.Chemi.Phys.，1997，107（21）：9264.

［5］ Liu C，Zeng D L.The effect factor of surface tension of liquid／vapor in molecular dynamics simulation［J］.Journal of Chongqing University：Nat.Sci.ED.，2002，25（4）：76（in Chinese）［刘朝，曾丹苓.汽液界面表面张力模拟中的影响因素［J］.重庆大学学报：自然科学版，2002，25（4）：76.

［6］ Rapaport D C.The art of molecular dynamics simulation［M］.Cambridge：Cambridge University Press，1995.

［7］ Nijmeijer M J P，Bakker A F，Bruin C，et al.A molecular dynamics simulation of the Lennard-Jones liquid–vapor interface［J］.J.Chem.Phys.，1988，89（6）：3789.

［8］ Enders S，Kahl H，Mecke M，et al.Molecular dynamics simulation of the liquid–vapor interface：I.The orientational profile of 2-center Lennard–Jones and of Stockmayer fluid molecules［J］.Journal of Molecular Liquids，2004，115：29.

［9］ Zhdanov E R，Fakhretdinov I A.Molecular dynamics simulation of the liquid–vapor interface of binary mixtures［J］.Journal of Molecular Liquids，2005，120：51.

［10］ Zeng D L，Ao Y，Zhang X M，et al.Engineering thermodynamics［M］.Beijing：Higher Education Press，2002（in Chinese）［曾丹苓，敖越，张新铭，等.工程热力学［M］.北京：高等教育出版社，2002］

［11］ Ma Q F，Fang R S.Practical thermal physical properties manual［M］.Beijing：China Agricultural Mechanical Press，1986（in Chinese）［马庆芳，方荣生.实用热物理性质手册［M］.北京：中国农业机械出版社，1986］