双外场对费米气体Joule-Thomson效应的调控
2014-03-20孙彦清龙姝明黄朝军娄本浊
孙彦清,龙姝明,黄朝军,娄本浊
(陕西理工学院物理与电信工程学院,汉中723000)
1 引 言
近年来,囚禁超冷玻色气体、超冷费米气体的理论和实验研究取得了一系列成果,极大地激发了相关学者对超冷量子气体的研究热情.有学者对囚禁在谐振势场中的玻色-爱因斯坦凝聚、微弱电场中理想费米体系的热容量和化学势、磁场中非广延相对论理想费米体系的统计性质、一般势阱之中(T ≠0K)理想费米气体的空间囚禁范围、谐振势中自旋极化理想费米气体的热力学性质等进行了大量的研究[1-6].关于有弱相互作用的量子体系,有学者对于囚禁在谐振势中的费米气体热力学性质、简并费米气体坍塌条件、6Li原子激光的输出、外势中费米体系密度、简并费米气体的稳定性以及s波和p波作用的影响、谐振势和幂函数势中费米气体的热力学性质、强磁场中费米气体的热力学性质和超冷费米气体的相对论效应、超流氦(HeⅡ)及弱相互作用费米气体和玻色气体的Joule-Thomson 系数等问题开展了的研究,取得了一系列重要的研究成果[7-19].
关于量子体系的现有研究,主要讨论的是量子系统在单外场中的热力学性质,关于双外场中量子系统热力学性质的研究较少.文献[20]研究均匀电场和谐振场共同约束下的带电费米系统,发现在双外场约束下的系统具有高温弱简并效应和分数维运动空间效应.为深入研究复杂时空分布的外场对物质体系热力学性质的影响、实验上选择最佳外势阱的形式及相关物理参数、探索新材料提供思路和理论参考,我们以处于均匀电场和谐振场中的带电费米粒子系统(忽略粒子间的相互作用后,可视为理想费米气体系统)为对象,研究双外场对系统Joule-Thomson 系数的调控作用.在满足Thomas-Fermi半经典近似的条件下,给出匀强电场和三维谐振场中的带电费米粒子系统的化学势、状态方程和Joule-Thomson系数的解析表达式,分析有限温度范围内双外场对系统Joule-Thomson系数的调控作用.
2 双外场中费米气体的化学势和状态方程
质量为m、带电量为q的N 个费米粒子在三维各向同性谐振场(振动频率为ω)和沿x轴方向的均匀电场E 构建的双外场中运动.假定粒子数密度低,可以忽略粒子间相互作用,无相互作用的N 个费米粒子与外场组成的系统可以视为理想费米气体,其体积为V,气体内能为U.单个费米粒子的能量可表示为
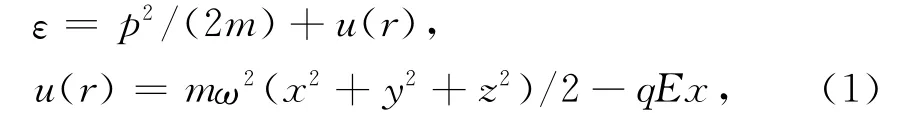
式中p2/(2m)为费米粒子的动能,u(r)为粒子在谐振场和均匀电场中的势能.
在原子气体的囚禁实验中,通常满足粒子数足够多,粒子热运动动能远大于能级间隔,所以Thomas-Fermi半径典近似是适用的[21],用相空间积分代替量子态求和,则受外电场和谐振场约束的费米气体在等能量曲面ε≥0 内的量子态数Ω(ε)及量子态密度D(ε)分别为

式(2)中ħ=h/(2π)是约化普朗克常量,g 为系统中粒子的自旋简并度,与其内部结构有关.自由理想 费 米 粒 子 系 统 的 态 密 度 D(ε)= 2πgV(2m/h2)3/2ε1/2依赖于能量的1/2 次幂,与自由理想费米粒子系统不同,双外场中的理想费米粒子系统的量子态密度依赖于能量的2次幂,而且与电场强度和谐振场频率都密切相关.
据统计力学原理,在均匀电场和谐振场中运动的费米粒子的平均占有数为
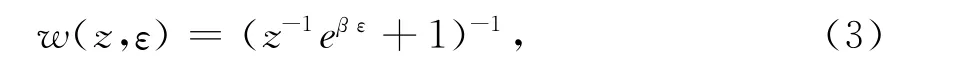
式中z=eβμ=eμ/kT为理想费米气体的逸度,β=1/(kT),k 为玻耳兹曼常数,T 为热力学温度.为计算费米粒子系统的热力学量需要定义费米积分
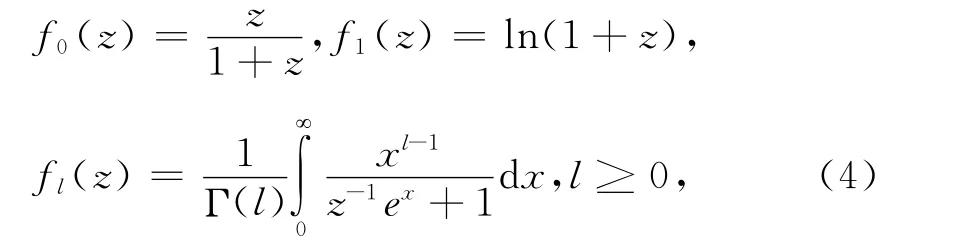
可以证明费米积分有下面的导数性质

z很大时(对应低温区),l<5的费米积分近似为
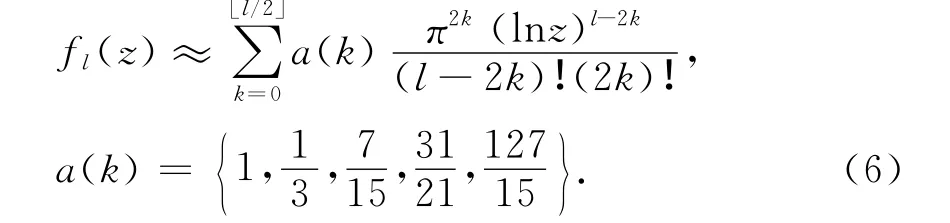
其中[l/2]表示对l/2取整.取l=1~4得到费米积分大z值近似



据式(6)和式(8)并用迭代算法证明,如果费米粒子取为电子,则粒子数不变的带电费米粒子系统在外场中的费米能量μF和化学势μ(大z 值近似)分别为(sF=α/μF)

取q=1.602×10-19C,w=2π×107Hz,N=6.02×1023,g=1,分别画出费米能量μF随外电场E 变化和随粒子质量变化的曲线(见图1).

图1 费米能量随外电场和粒子质量的变化曲线(a)m=me=9.11×10-28 g,外电场E 对费米能量的调控;(b)E=500V/m,费米能量随粒子质量的变化Fig.1 The curves of the Fermi energy with the external electric field and particle mass changes
式(10)和图1表明双外场对费米能量有明显的调控作用.外电场越强,系统费米能量越低.因α 随质量增加而减小,图1(b)表明,外场中费米粒子气体的费米能量μF随粒子质量的增加而快速增加.
若取m=9.11×10-28g,N=6.02×1023,ω=2π×107Hz,α=5.569eV,μF=1.969eV,画出带电费米子系统化学势随温度变化的曲线(见图2).由图2显见,外场对带电费米子系统的化学势有调控作用.外电场越强,带电费米子系统的化学势和费米能量值越小,并且系统的化学势由正变负的临界温度越低.

图2 双外场中的带电费米粒子系统化学势随温度变化曲线(a)E=500V/m,μF=1.969eV,化学势由正变负的临界温度Tμ=24800K;(b)E=1000V/m,μF=0.1704eV,化学势由正变负的临界温度Tμ=12200KFig.2 The curves of the chemical potential with the temperature changes
外电场E=500V/m 时,由图2(a)结合计算可知,T<600K 时,外场中的带电费米子系统的化学势μ/(kT)≈μF/(kT)>38,即化学势μ 在很大温度范围内能近似等于系统的费米能量μF=1.969eV,考虑这一结果,我们可以导出外场中的带电费米子系统内能随温度变化的显函数关系是(其中,α/μF是由外场决定的常数)

据热力学理论PV=2U/3,结合式(11)得到双外场中费米气体的状态方程(即气体的压强P 与体积V 之积)为

3 双外场中费米气体的Joule-Thomson系数
由式(12)得到

保持P 不变对式(13)关于T 求导可得

根据H =U+PV,得费米气体的焓

保持P 不变对式(15)关于T 求导,可得
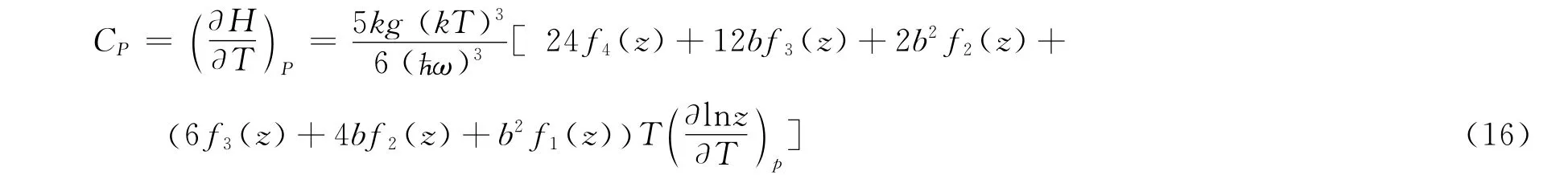
对式(8)保持气体系统粒子数N 和压强P 不变关于T 求导,得到

引用费米积分大z值近似,上式简化为

由统计力学理论可知费米子气体的Joule-Thomson系数为

式中,μJT、CP、H 分别是费米气体系统的焦耳-汤姆逊系数、定压热容量、状态函数焓.联立式(13)~(18)得到均匀电场和谐振场中带电费米粒子系统的Joule-Thomson系数

4 双外场对焦汤系数的调控作用

引用式(7)、(17)、(19)得到带电费米粒子系统的焦汤系数μJT(大z值近似)为

若取P=20dn/cm2,m=9.11×10-28g,N=6.02×1023,ω=2π×107Hz,α=5.569eV,μF=1.969eV,依据式(20),可以画出如图3所示的带电费米粒子系统的焦汤系数随温度变化的曲线.注意式(20)有效的温度范围由μ/(kT)>>1 决定.T=8000K 时,μ/(kT)=2.56已经不能满足远大于一的条件了.

图3 外场中的带电费米粒子系统的焦汤系数随温度变化曲线(a)E=500V/m,临界温度TC=8000K;(b)E=1000V/m,临界温度TC=1200KFig.3 The curves of the Joule-Thomson coefficient with the temperature changes
图3表明,低温情况下均匀电场和谐振场中带电费米粒子系统的Joule-Thomson效应为负效应.随着温度的升高,系统的焦汤效应将由负变正,其临界温度受外加电场调控,外电场越强,临界温度越低.计算表明,粒子质量增加时,系统的费米能量增加,系统的焦汤系数临界温度也将增加.
5 结 语
(1)匀强电场和谐振场构成的双外场对带电费米粒子系统的焦耳-汤姆逊系数及所有热力学量有十分明显的调控作用.这表明,可以用加双外场的方法改变带电费米粒子系统的温度、压强、体积等.
(2)外电场的存在会使带电费米粒子系统产生焦耳-汤姆逊正效应.随着温度的升高,带电费米粒子系统的焦耳-汤姆逊系数的值逐渐由负变正,而且临界温度TC随外电场增强而降低.
(3)费米粒子系统的焦耳-汤姆逊系数由负变正的临界温度TC随粒子质量μ 增加而明显增加,这说明,大质量带电费米粒子系统要取得正焦耳-汤姆逊效应很困难.(4)费米粒子系统的化学势μ 随温度的升高,由正变负的临界温度Tμ随外电场的增加而明显降低.
[1] Anderson M H,Ensher J R,Matthews M R,et al.Observation of Bose-Einstein condensation in a dilute atomic vapor[J].Science,1995,269(5221):198.
[2] Bradley C C,Sackett C A,Tollett J J,et al.Evidence of Bose-Einstein condensation in an atomic gas with attractive interaction [J].Phys.Rev.Lett.,1995,75(9):1687.
[3] Davis K B,Mewes M O,Andrew M R,et al.Bose-Einstein condensation in a gas of sodium atoms[J].Phys.Rev.Lett.,1995,75(22):3969.
[4] Li X P,Liu W S,Zhang G F.Bose-Einstein Condensation in External Potential[J].Acta Sinica Quantum Optica,2003,9(1):27(in Chinese)[李秀平,刘文森,张国锋.外势场中玻色-爱因斯坦凝聚性质的研究[J].量子光学学报,2003,9(1):27]
[5] Sun Y Q,Long S M ,Huang C J,et al.Influence of homogeneous weak electric field on the heat capacity and chemical potential of charged fermion system[J].J.At.Mol.Phys.,2010,27(6):1200(in Chinese)[孙彦清,龙姝明,黄朝军,等.均匀微弱电场对带电费米子体系热容量和化学势的影响[J].原子与分子物理学报,2010,27(6):1200]
[6] Men F D,Wang H T,He X G,et al.Statistical Properties of non-extensive relativistic Fermi system in a magnetic field[J].J.At.Mol.Phys.,2011,28(6):1143(in Chinese)[门福殿,王海堂,何晓刚,等.磁场中非广延相对论费米系统的统计性质[J].原子与分子物理学报,2011,28(6):1143]
[7] Modugno G,Roati G,Riboli F,et al.Collapse of a degenerate Fermi gas[J].Science,2002,297(5590):2240.
[8] Yin J P,Wang Z L.Experiment of Bose-Einstein Condensation and its recent progress[J].Prog.Phys.,2005,25(3):235(in Chinese)[印建平,王正岭.玻色—爱因斯坦凝聚(BEC)实验及其最新进展[J].物理学进展,2005,25(3):235]
[9] Yuan D Q.Maximum trap range and equation of state for Fermi gas in potential trap[J].Acta Phys.Sin.,2011,60(6):060509 (in Chinese)[袁 都 奇.Fermi气体在势阱中的最大囚禁范围与状态方程[J].物理学报,2011,60(6):060509]
[10] Noronha J M B,Toms D J.The specific heat of a trapped Fermi gas:an analytical approach[J].Phys.Lett.A,2000,267(4):276.
[11] Butts D A,Rokhsar D S.Trapped Fermi gas[J].Phys.Rev.A,1997,55(6):4346.
[12] Bruun G M,Burnett K.Interacting Fermi gas in a harmonic trap[J].Phys.Rev.A,1998,58(3):2427.
[13] Oliva J.Density profile of the weakly interacting Fermi gas confined in a potential well:Nonzero temperature[J].Phys.Rev.B,1989,39(7):4204.
[14] Roth R,Feldmeie H.Effective s-and p-wave contact interactions in trapped degenerate Fermi gases[J].Phys.Rev.A,2001,64(4):043603.
[15] Men F D,He X G,Liu H,et al.Relativistic paramagnetism of a weakly interacting Fermi gas[J].J.At.Mol.Phys.,2011,28(4):760(in Chinese)[门福殿,何晓刚,刘慧,等.弱相互作用费米气体的相对论顺磁性[J].原子与分子物理学报,2011,28(4):760]
[16] Men F D,Wang B F,He X G,et al.Thermodynamic properties of a weakly interacting Fermi gas in a strong magnetic field[J].Acta Phys.Sin,2011,60(8):080501(in Chinese)[门福殿,王炳福,何晓刚,等.强磁场中弱相互作用费米气体的热力学性质[J].物理学报,2011,60(8):080501]
[17] Men F D,He X G,Zhou Y,et al.Relativistic effect of ultracold Fermi gas in a strong magnetic field[J].Acta Phys.Sin.,2011,60(10):100502(in Chinese)[门福殿,何晓刚,周勇,等.强磁场中超冷费米气体的相对论效应[J].物理学报,2011,60(10):100502]
[18] Chen Y,Lu X S,Gu A Z.Study on the Joule-Thomson Coefficients of Superfluid Helium[J].Cryogenics &Superconductivity,2004,32(4):19(in Chinese)[陈煜,鲁雪生,顾安忠.超 流氦的Joule-Thomson系数研究[J].低温与超导,2004,32(4):19]
[19] Yuan D Q,Wang C J.Joule– Thomson coefficients of weakly interacting Fermi gases and Bose gases[J].Phys.Lett.A.2007,363:487.
[20] Sun Y Q,Hang C J,Long S M,et al.The high temperature weak degeneration effect of charged particle system in two external field[J].Acta Phys.Sin.,2009,58(11):7502(in Chinese)[孙彦清,黄朝军,龙姝明,等.带电粒子系统在双外场中的高温弱简并效应[J].物理学报,2009,58(11):7502]
[21] Chou T T,Yang C N,Yu L H.Bose-Einstein condensation of atoms in a trap[J].Phys.Rev.A,1996,53:4257.
