AunLa（n=1～8）团簇的密度泛函研究

张建婷，李 晶，盛 勇

（四川大学材料科学与工程学院，成都610065）

1 Introduction

Due to their special physical and chemical properties，the gold clusters have been an important subject of theoretical computation studies for charactering the ground-state geometrical structures，electronic and magnetic properties as well as their relative stabilities.Au clusters doped with transition mental atom have been studied extensively［1-7］.Die et al.［8，9］investigated the geometrical structures，relative stabilities，and magnetic moments of AunFe（n=1～7）clusters and AunSc（n=1～8）clusters by density functional theory（DFT）.Yang et al.［10］studied the AunRh（n=1～8）clusters，and found that the groundstate clusters have planar structures except for n=5and 8.The analysis of stability shows that the clusters with even numbers of atoms are more stable than the clusters with odd numbers of atoms.It is interesting that AunIr（n=1～8）clusters have the opposite stability tendency.For AunIr（n=1～8）clusters，the even-number AunIr clusters are more stable［11］.

The geometrical configurations and electronic properties of La-doped gold cluster have been investigated by Zhao et al.［12］by using DFT（PW91PW91／CEP-121G）.In this paper，based on the study of the geometry configurations，we make a further research on the stabilities and electron properties of the ground-state structures.The goal of this study is to provide theoretical in sight for supporting the preparation，characterization and application of rare earth element doped gold clusters.

2 Computational method

The structure optimizations and energy calculations of AunLa（n=1～8）clusters were carried out by using the DFT （B3LYP） with LANL2DZ basis sets.All the computations were accomplished by Gaussian03program package［13］.In order to find the lowest energy structure of AunLa（n=1～8）clusters，various possible initial configurations were considered.These initial configurations are optimized at all possible spin multiplicities.The structures which have the lowest energy without imaginary frequency are chosen as the stable structures.In all calculations，the convergence criteria of energy，force and displacement are set to 1×10-7a.u.，1×10-4a.u.／Bohr and 1×10-3Bohr respectively.

In order to estimate theaccuracy of the computational method，we calculated the bond length and vibrational frequency of Au2and La2.Our calculated results of 2.57Åand 162cm-1for Au2，2.91Åand 150cm-1for La2are in good agreement with 2.53 Å and 171cm-1for Au2from Ref.［14］and 2.91Åand 150cm-1for La2from Ref.［15］.These results indicate the calculation method we have chosen to describe the AunLa（n=1～8）clusters system is with reasonable accuracy.

3 Results and discussion

3.1 Geometry

For theAunLa（n=1～8）clusters，the lowest energy structure and the low-lying isomers for each AunLa（n=1～8）clusters are listed in Fig.1.The darker spheres denote the La atom，while the lighter spheres represent the Au atom.According to the energies from low to high，the isomers are designated by na，nb，nc，nd.（n refers to the number of Au atoms in AunLa clusters）.Meanwhile，the geometric parameters of the AunLa（n=1～8）clusters in the lowest-energy are given in Table 1.

Theground-state structure of AuLa is linear with triplet spin state.The lowest energy structure of Au2La is the planar 2astructure with C2v.The triangle 2bisomer and linear 2cisomer are less table than the ground-state by 1.5693eV and 1.7967 eV，respectively. Three-dimensional structure appears at n=3.Using La atom replacement the ground-state structure of pure Au4cluster［14］obtained the most stable structure of Au3La cluster 3a.The C2vrhombus isomer 3band the broken line structure of 3care above the ground state 3aenergy by 1.7324eV and 2.1112 eV respectively.As to the Au4La cluster，both the planar and three-dimensional structures are obtained.In the ground-state structure of Au4La，La atom occupies the apex position of tetrahedron and on this basis connects one Au atom.The energy of 4bisomer is 0.0177eV higher than the 4a structure.While the energy of planar structure 4c is higher than that of 4b.Starting from Au5La，the stable isomers are all three-dimensional structure.As to the lowest energy structure of Au5La clusters 5a，La atom occupies the center position，other Au atoms unfold center around it.The 5bisomer can be regarded as adding one more Au atom to the 4bisomer center around La atom.For the Au6La cluster，connecting an Au atom at the top of the ground-state Au5La cluster obtained the 6astructure.As to 6bisomer，La atom occupies the tetrahedron vertex position and two Au atoms connected to it separately.The groundstate of Au7La cluster，the La atom occupies the center position.Three Au atoms bond together on the top of the structure，others arrange in a ring.The isomer 7bcan be seen as based on the 6aisomer，connecting an Au atom to the lateral of Au ring.The energies of the metastable structures 7band 7care higher than the ground-state by 0.1015eV and 0.4388eV respectively.The shape difference between 7dand 7ais that four Au atoms are arranged in a quadrate not a ring.By connecting two Au atoms to the 6aconfiguration，the most stable structure of Au8La cluster is obtained.For the 8bisomer，La atom connects a trigonal bipyramid on the left and a fan-shaped on the right.The energy of 8cis higher than the 8a by 0.2844eV.The 8disomer can be considered as connecting a tetrahedron to the ground-state of Au5La.

From the above analysis，the most stable structures of AunLa（n=1～8）clusters have the three-dimensional structure except n=1，2.The La atoms tend to bind more Au atoms in the lowest-energy geometries.This is consistent with Ref.［12］.This may be ascribed to the fact that valence shell of the La atom is 5d16s2.For lanthanide compound，the powerful bonding orbital is 5d［16］.The d orbitals are not completely filled in La atom，so it have more position to bind Au atoms and tends to occupy the most highly coordinate position.

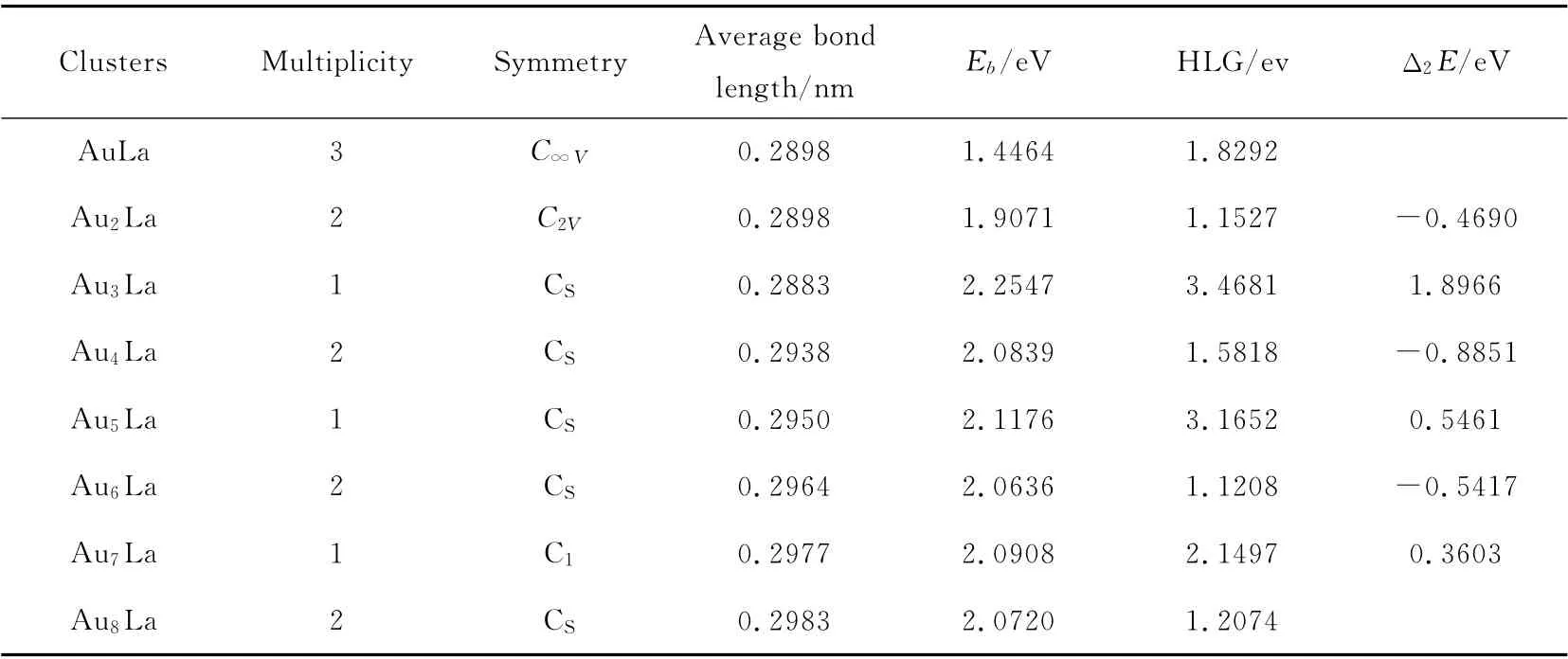
Table 1 Geometric parameters and energies for the ground-state AunLa（n=1～8）clusters

3.2 Stability

In order to investigate the stabilities of AunLa（n=1～8）clusters for ground-state structures，we report in this section the averaged binding energies（Eb），the second-order difference in energy（Δ2E）and the gap between the highest occupied molecular orbital（HOMO）and the lowest unoccupied molecular orbital（LUMO）.

The averaged binding energies（Eb）and the second-order difference in energy（Δ2E）are respectively defined as：

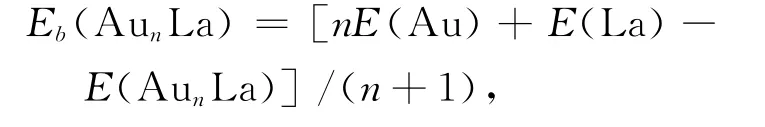
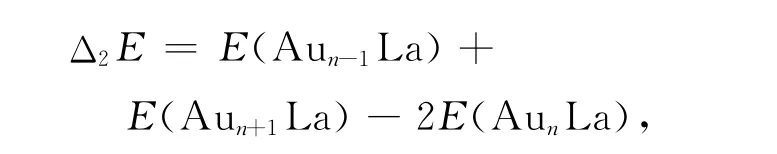
where E represent the corresponding energy of ground state clusters respectively.The calculated result is showed in Fig.2.It can be seen from the Fig.2，the averaged binding energy of n=1is lower compared to other clusters.It increases quickly fromn=2and reaches the peak at n=3.The averaged binding energies have small changes for n=4～8.This manifests that Au3La possesses higher stability. The second-order difference in energy（Δ2E）is used to reflect the relative stability of the clusters.The higher value ofΔ2Eindicates the cluster is more stable.For the ground-state AunLa clusters，the curve shows that the second-order difference energies of Au3La，Au5La and Au7La clusters are higher than the neighboring clusters.Moreover，Au3La has the largest value of 1.8966eV／atom.However，there are no obvious peaks among the three clusters in Ref.［12］.This maybe ascribe to all of their geometric symmetries are C1.

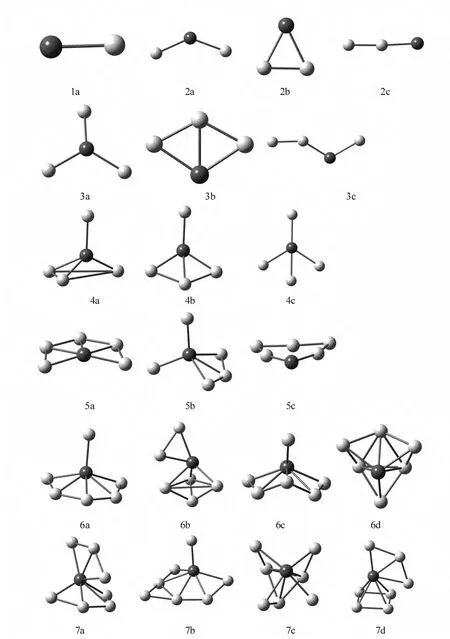
Fig.1 Geometries of AunLa（n=1～8）clusters

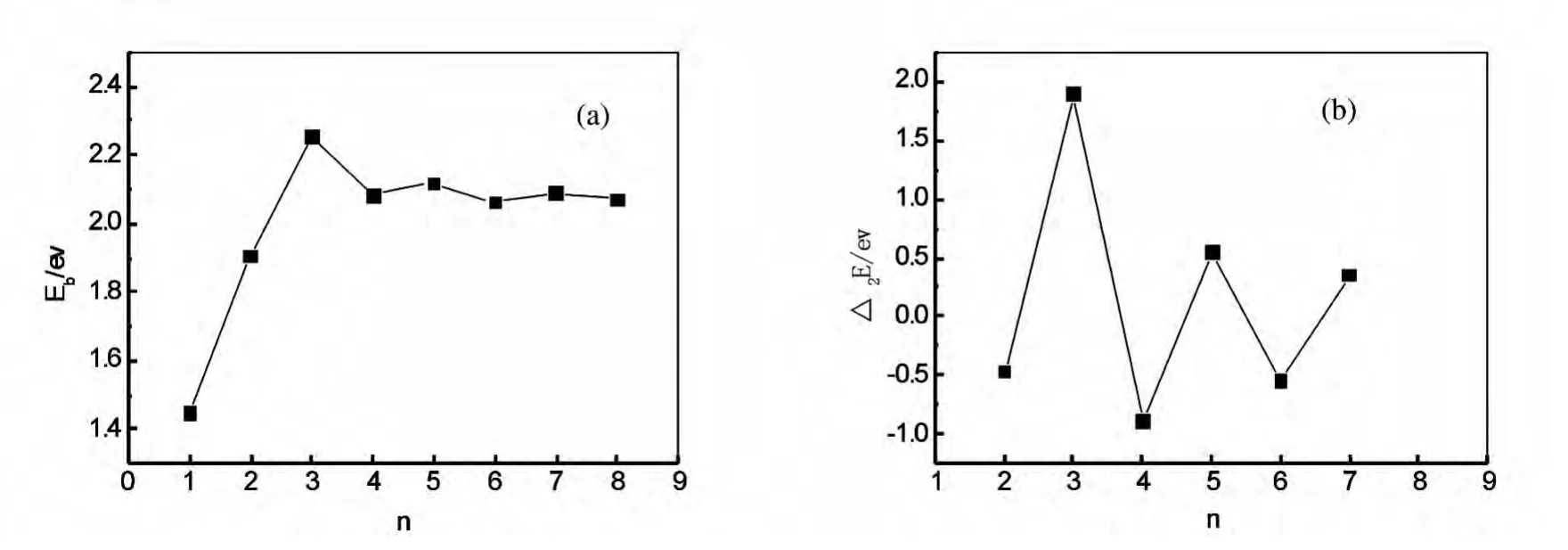
Fig.2 （a）Average binding energies of clusters and（b）the second difference of energies for the ground-state AunLa（n=1～8）clusters

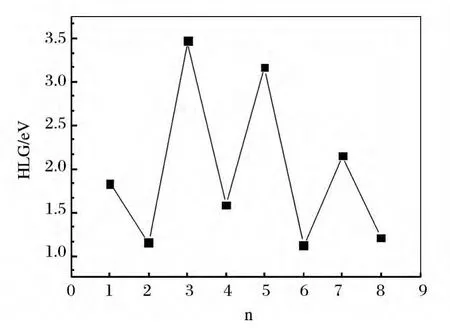
Fig.3 Energy gaps for the ground-state AunLa（n=1～8）clusters

For clusters，the HOMO-LUMO energy gap（Eg）reflects the ability of an electron to jump from the occupied orbital to the unoccupied orbital.In general，the larger value of the energy gap，the more stable of the molecular.The HOMOLUMO energy gap（Eg）results are summarized in Fig.3.The curve shows odd-even oscillations.It indicates that the even sized clusters are more stable than the odd sized clusters.Moreover，the HOMO-LUMO orbital diagrams of AunLa clusters are displayed in Fig.4.This gives us an intuitive understanding of the bonding patterns of Au and La atoms.

From what we have discussed above，Eb，Δ2E and Egshow the odd-even oscillations.This phenomenon can be explained by the electron paring effect.The valence shell of Au atom is 5d106s1，the d orbitals of Au atom are completely filled and there is just one electron on its s orbitals.For La atom the valence shell is 5d16s2.When combined with Au atom，it provides one or three valence electrons.The total number of bonding electrons of AunLa is（1+n）or（3+n）.When nis even，（1+n）and（3+n）are odd.AunLa cluster has an unpaired single electron.When n is odd，both the（1+n）and（3+n）are even.Namely，the even size clusters has an even total number valence electrons and its HOMO is doubly occupied.The electron in a doubly occupied HOMO with stronger effective core potential due to the electron screening is weaker for electrons in the same orbital than that for inner-shell electrons.Thus，the binding energy of valence electrons in clusters of even size is higher than that in an odd size one.Interestingly，the obvious peak is also located at n=3.It shows that the Au3La cluster with higher energy gap is less reactive.

3.3 Electronic properties and hardness

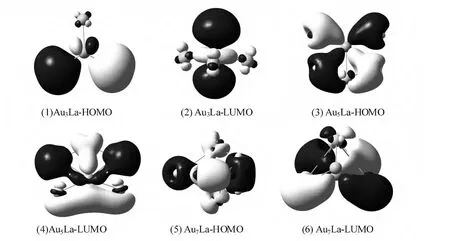
Fig.4 The HOMO and LUMO orbitals of AunLa（n=1～8）clusters

In cluster physics，the ionization energy（IP）and the electron affinity energy（EA）are used to describe the electronic properties of the cluster.The IP for the cluster is equal to the bonding en-ergy of a neutral cluster lost an electron.The larger the value，the more stable the cluster is.The EA reflects the ability of a neutral cluster receiving an electron，the higher value of EA indicates the cluster is more active.IP and EA are defined as

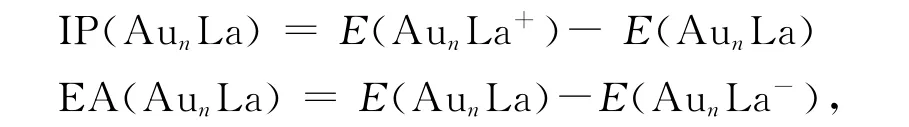
whereE（AunLa+），E（AunLa-）and E（AunLa）represent the energies of AunLa+，AunLaand AunLa clusters respectively.The calculated results of the ground-state structure are showed in Fig.5.It can be seen from the Fig.5that the biggest value of IP is Au3La cluster，which is consistent with the analyses in section 3.1and 3.2.As to EA，the value of Au3La is slightly higher than Au2La，may be due to the Au2La cluster with C2vsymmetrical geometry and the different spin states.However，for Au5La and Au7La clusters，their values are lower compared with their neighboring clusters.They are more stable.

With the IP and EA values，the chemical hardnessηcan be studied.The chemical hardness ηdefined asη≈（IP-EA）／2，which shows the ability of molecules to accept an electron.Higher values of hardness indicate the molecule does not easily accept electrons.The results are given in Table 2，and the size dependence ofηfor the ground-state structure AunLa clusters is shown in Fig.5.The curve shows an oscillating behavior，the peaks appear at n=3，5，7.These clusters with even number of atoms are harder and more stable than their neighboring clusters.In addition，the Au3La cluster has the largest chemical hardness of 3.3738eV.

4 Conclusion

The geometrical structures，relative stabilities，and electronic properties of theAunLa（n=1～8）clusters have been investigated by using the hybrid density functional theory B3LYP with LANL2DZ basis sets.The conclusions are summarized as follows.

1）The most stable structures of AunLa（n=1～8）clusters have the three-dimensional structures except for AuLa and Au2La.The La atoms tend to bind more Au atoms in the lowest-energy geometries.

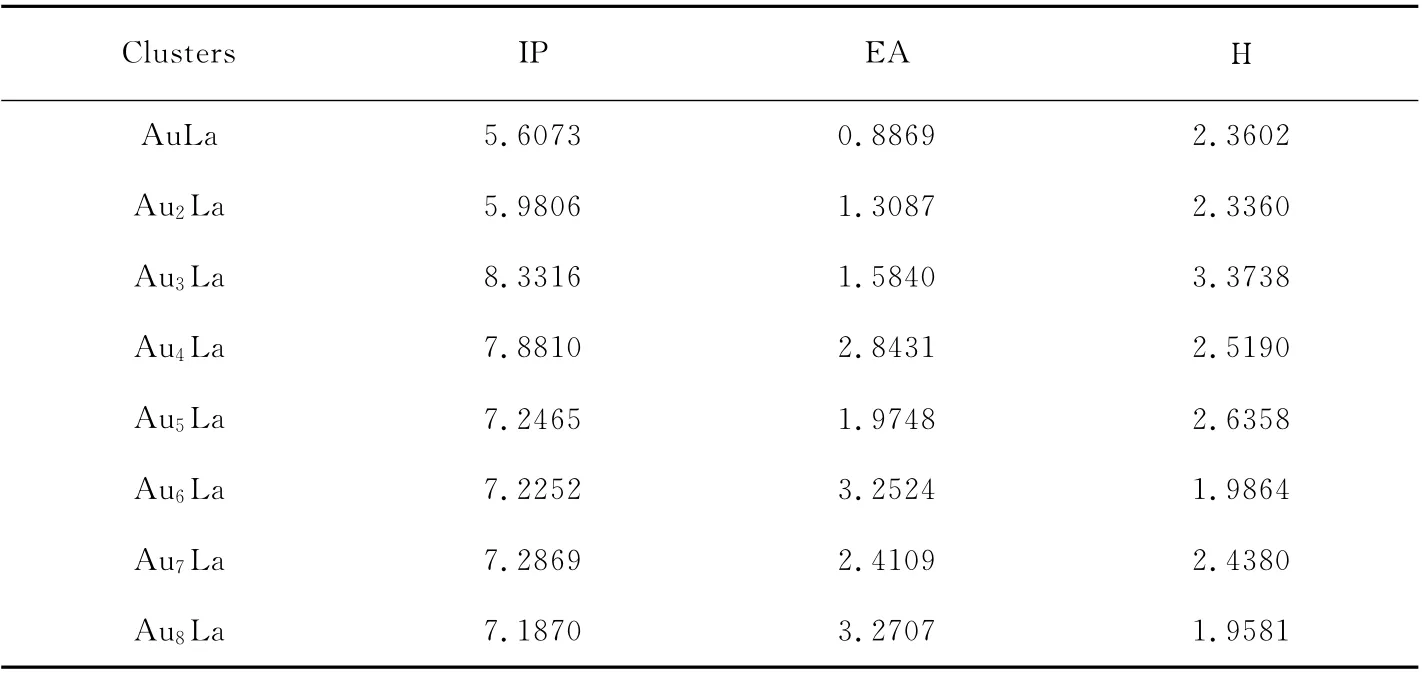
Table 2 Ionization potential（IP），electron affinity（EA）and hardness for the ground-state AunLa（n=1～8）clusters

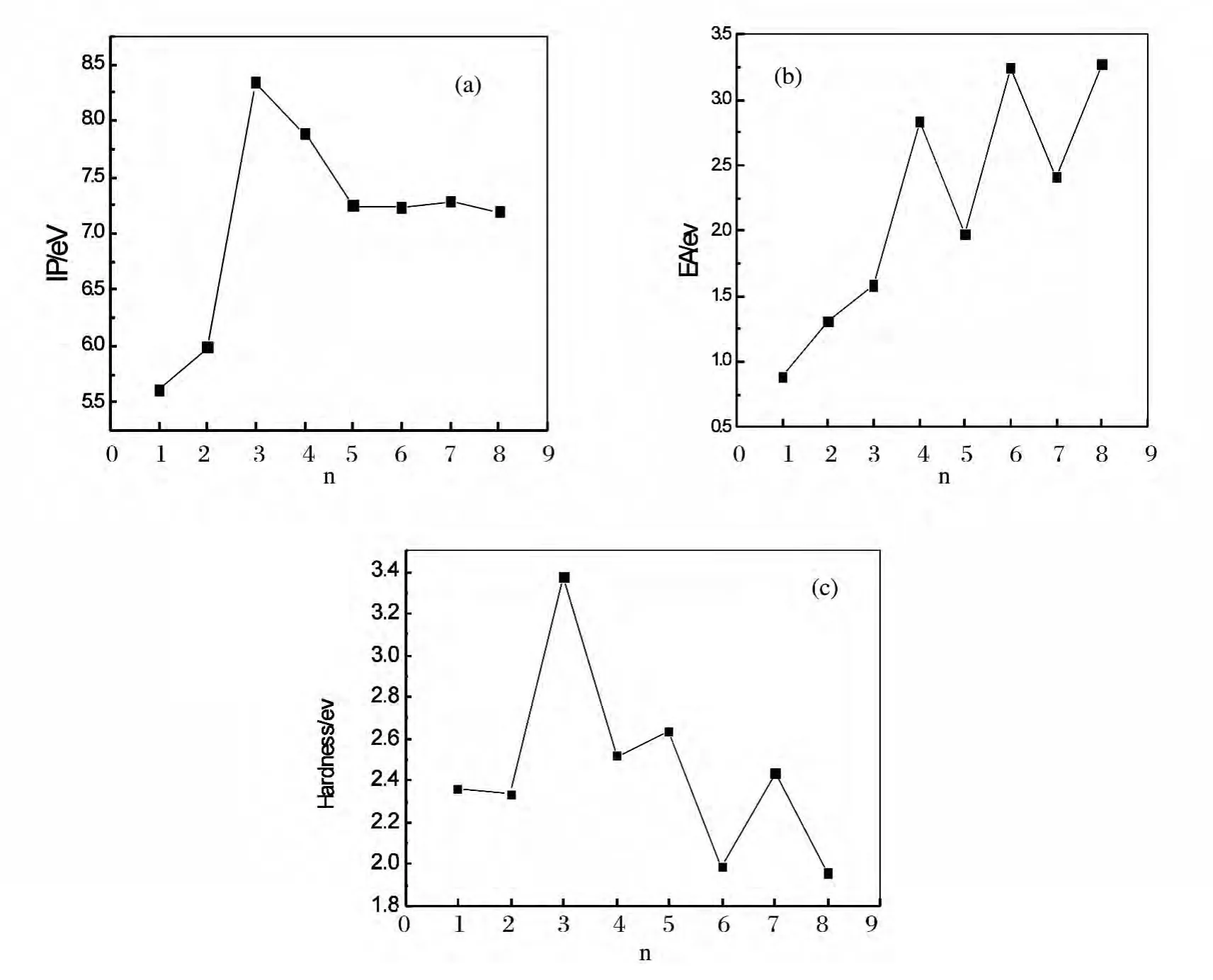
Fig.5 （a）The ionization potential（IP），（b）the electron affinity（EA）and（c）the chemical hardness for the lowest energy structures of AunLa（n=1～8）clusters

2）For the ground-state structures of AunLa（n=1～8）clusters，the analyses of the secondorder difference in energy，the HOMO-LUMO energy gap and the hardness exhibit an odd-even oscillation behavior.Except the AuLa，the AunLa（n=2～8）clusters with even-number of atoms are more stable than the neighboring clusters with odd-number of atoms.The Au3La cluster is the most sable cluster as shown in all the curves of Eb，energy gaps andthe hardness.

［1］ Mao H P，Wang H Y，Ni Y，et al.Geometries and electronic properties of Aun（n=2～9）clusters［J］.Acta Phys.Sin.，2004，56：1766（in Chinese）

［2］ Ren L，Cheng L J.Structural prediction of（Au20）N（N=2～40）clusters and their building-up principle［J］.Comput.Theor.Chem.，2012，984：142.

［3］ Yang A，Fa W，Dong J M.Geometrical structures and vibrational spectroscopy of medium-sized neutral Aun（n=17～26）clusters［J］.Phys.Let.A，2010，374：4506.

［4］ Zhao L X，Cao T T，Feng X J，et al.A theoretical study of neutral and anionic Au5Al clusters［J］.J.Mol.Struct.：Theochem.，2009，895：92.

［5］ Xu Y，Xu C，Zhou T，Cheng C，et al.Nonlinear optical properties of Aun-mMm（M = Ag，Cu；m=1，2）clusters［J］.J.Mol.Struct.：Theochem.，2009，893：88.

［6］ Die D，Kuang X Y.Theoretical study of geometrical structures and electronic properties for Co＠Aun（n=1～8）clusters［J］.J.At.Mol.Phys.（原子与分子物理学报），2012，29（2）：267（in Chinese）

［7］ Guo J J，Yang J X，Die D.Ab initio study of small AunPd2（n =1～4）clusters［J］.Phys.B，2005，367：158.

［8］ Die D，Kuang X Y，Guo J J，et al.First-principle study of AunFe（n=1～7）clusters［J］.J.Mol.Struct.：Theochem.，2009，902：54.

［9］ Die D，Kuang X Y，Zhu B，et al.Geometrical，elec-tronic，and magnetic properties of small AunSc（n=1～8）clusters［J］.Phys.B，2011，406：3160.

［10］ Yang J X，Wei C F，Guo J J.Density functional study of AunRh（n=1～8）clusters［J］.Phys.B，2010，405：4892.

［11］ Yang J X，Guo J J，Die D.Ab initio study of AunIr（n=1～8）clusters［J］.Comput.Theor.Chem.，2011，963：435.

［12］ Zhao L X，Feng X J，Zhang M，et al.Structure growth sequences and electronic properties of lanthanum-doped-gold clusters［J］.J.Clust.Sci.，2010，21：701.

［13］ Frisch M J，Trucks G W，Schlegel H B，et al.Gaussian 03，Revision A.1，Pittsburgh，PA：Gaussian，Inc.，2003.

［14］ Ajanta Deka，Ramesh C.Deka.Structure and electronic properties of stable Aun（n=2～13）clusters：a density study［J］.J.Mol.Struct.：Theochem.，2008，870：83.

［15］ Yang Z，Wang Y X，Guo A M，et al.The structures and electronic properties of Lanand LanO（n=2～12）clusters［J］.Chem.Phys.，2009，359：82.

［16］ Xu G X，Wang X Y.Material structure［M］.Beijing：Science Press，2010：147（in Chinese）