弱相互作用玻色-爱因斯坦凝聚体中涡旋动力学与量子混沌轨道

崇桂书，Borondo F

（1.湖南大学物理与微电子科学学院，长沙410082；2.Departmento de Química，Universidad Autónoma de Madrid，Cantoblanco-28049 Madrid，Spain）

1 Introduction

Zeros of the wave function in a certain regime indicates singular wave structures，which contain topological wave front dislocations.There are ubiquitous in many branches of classical and quantum physics.Screw dislocations，or vortices，are a common dislocation type.In classical physics，properties of vortices have been extensively investigated in many fields，such as cosmology［1，2］，hydrodynamics［3］，or non-linear optics［4］，just to name a few.Quantum mechanically，the vortices that are concerned with happen in the（peculiar）probability fluid［5，6］.This type of vortices have been studied in the past in connection with superfluidity［7，8］and superconductivity［9］. More recently，this kind of quantized vortex has been experimentally observed in the quantum fluids associated to Bose-Einstein condensates（BEC）［10-17］.Single vortex line，vortex lattices and even multiply charged vortices can be created by using Raman transition phase-imprinting methods［10］，rotating the system with a“laser spoon”［11，13，18，19］or applying topological phase engineering［20］，respectively.Moreover，a number of theoretical and experimental investigations have been carried out on the features of these vortices，such as the stability and dynamics of single vortex or different vortex clusters in non-rotating［21-25］and rotating［26］single component BEC，and even in twospecies BECs［27-30］.

A very straightforward way to study quantum vortices is to use the hydrodynamic-based formulation of quantum mechanics introduced in the 1950s by David Bohm［31］in an attempt to solve some of interpretational difficulties of the standard version［32］.One of the resulting equations（see next Section）allows the definition of“quantum trajectories”（QTs）which，according to the probabilistic interpretation of quantum mechanics，represent the paths along which the probability flows in the“quantum fluid”.Very recently the so-called Bohmian mechanics（BM），which represents a true theory of quantum mo-tion［33］，has experienced an increased popularity，triggered mostly by practical interest［34-41］.The reason for this being it combines the accuracy of the standard quantum theory with an intuitive insight derived from the causal trajectory formulation，this providing apowerful tool to shed light on the physical mechanisms underlying microscopic phenomena.An intense debate exists，however，about the “reality”of such trajectories［42］.In the Bohmian theory，QTs are determined by not only the external potential but also a quantum potential determined from the wave function.As a consequence of quantum interferences in the wave functions the quantum potential can be very intricate，and it plays an important role in the relation of the QTs with the quantum probability.In particular，when the wave function vanishes the quantum potential tends to infinity，and then QTs are forbidden in the corresponding region.This is obviously in agreement with the results of standard quantum mechanics according to which vanishing wave functions corresponds to null probability density.Another interesting point of BM，especially in relation with the present work，is that Frisk［43］and Wisniacki et al［38-40］have recently pointed out the possible relationship existing between vortices and chaos in the QTs.In particular，it has been established the functional relationship between vortex dynamics and QT ergodicity in the two-dimensional（2D）harmonic oscillator and rectangular billiard models［44］.

In the present paper，we consider a weakly interacting BEC system confined in a harmonic trap.This situation can be adequate described by a nonlinear Schrödinger equation as it has been experimentally shown.Using a variational method，we have computed solutions for different vortex clusters and analyzed the corresponding dynamics.Also，numerical simulations are presented，which are in good agreement with the analytical results.Based on the analytical solutions，the chaotic characteristics of the associated QTs are studied using stroboscopic Poincarésurfaces of section.Influences，which are caused by geometry shape of vortex moving orbit，nonlinear twobody interaction and vortex interaction，to the complexity of the QTs are discussed for the case of single vortex，vortex pairs and vortex dipole，respectively.

The organization of the paper is as follows.The model under study and the methodology are introduced in Sect.II.In it，the dynamical aspects of three different cases，namely a BEC with single vortex，a BEC with a pair of vortices，and a BEC with a vortex dipole，are considered both analytically and numerically.The chaotic QTs based on these vortex clusters are discussed in Sec.III.Finally，our conclusions are summarized in Sect.IV.

2 Vortices dynamics in weakly interacting BEC

2.1 Model and the hydrodynamic formalism

For a temperature well below the critical point，Bose-Einstein condensation occurs.In dilute and weakly interacting Bose gases，it is well known that the BEC dynamics can be well described by a Gross-Pitaevskii equation（GPE）in the mean-field theory framework，which can be described by

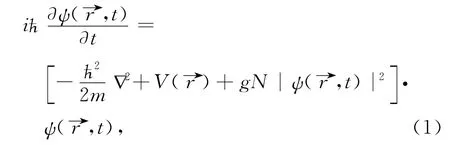
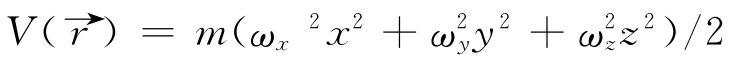
Now，following the usual technique in BM，we write the wave function，ψ，in polar form

where Rand Sare two time and position dependent real functions，given the amplitude and phase of the wave function，respectively.Substituting Eq.（3）into the dimensionless GPE（2），we recast the quantum theory into a＇hydrodynamical＇form，which is governed by

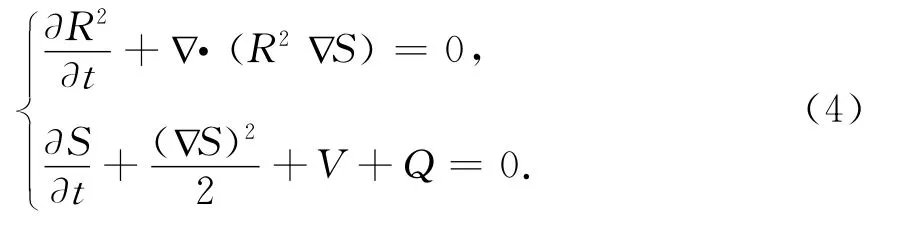
These two equations represent the continuity and“quantum”Hamilton-Jacobi（HJ）equations，respectively.Comparing to the classical HJ equation we see that an extra term，

determined by the quantum state and the two-body interaction，appears. This term is called the“quantum potential”，and it is responsible of introducing the quantum effects into the dynamics of the system.In analogy with the standard HJ theory，Eq.（4）allows the introduction of“quantum trajectories”for our system.These QTs can be obtained by integrating the corresponding velocity field

The quantum state is therefore defined，in this interpretation of quantum mechanics，by ψ（x，y，t），x（t），y（t），that evolve simultaneously in a deterministic way，withψacting as a pilot wave guiding the particles，each one of them starting at a different position.

2.2 Vortex dynamics in thevariational method

Let us concentrate now on the study of the dynamics of different vortex clusters in the nonrotational system defined in the previous subsection.If the vortices are initially located at positions rj= （xj，yj），the corresponding initial state can be well approximated in the form［22］

whereνj=（x-xj）=ip（y-yj），ψgsis the ground state wave function acting as a background，cis a normalizing constant，and p=±1represents the topological charges of the vortices.This approximation is valid when the vortices are not far away from the center of the condensate.Experimentally，such initial states can be prepared with the methods mentioned in the Introduction.

Presently，it is not known how to obtain an exact analytical solution for the vortex dynamics in the full GPE equation framework.However，when the interatomic interaction is very weak，i.e.small values of g2d，the Ritz minimization method can be used to get good approximate analytical solutions［21，45］.In this case，the following ansatz for the solution of GPE

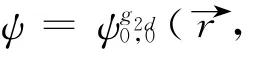
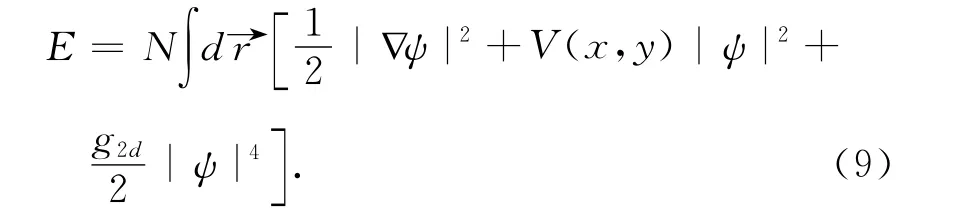
Using thevariational principle，δE／δσx，y=0，constantsσxandσycan be determined from the following two algebraic equations

The chemical potentials，μn，m，in Eq.（8）are calculated as

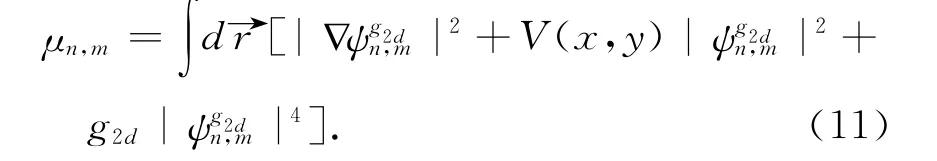
Now，the wave functions of Eq.（8）can then be used to expand the solutions for different vortices clusters，satisfying the initial condition（7）.As examples，the cases corresponding to a single vortex，a vortex pair，and a vortex dipole，will be considered in the present paper.

2.2.1 Single vortex

Assuming that a single vortex initially occupies theposition（x1，y1），the wave function can be written in the form

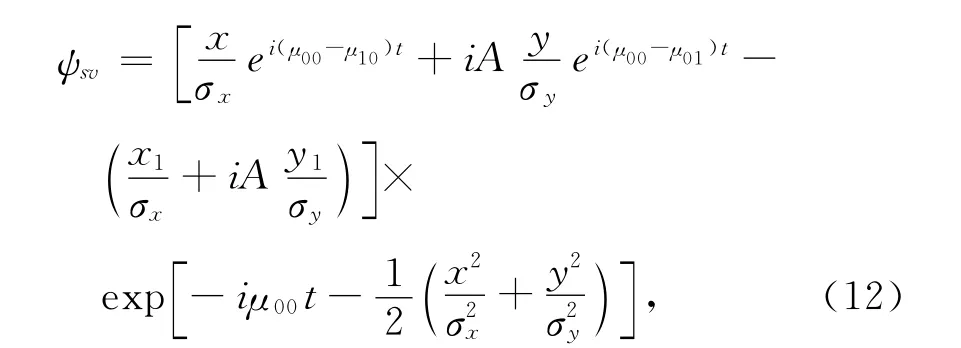
and analytically determine that the dynamics of this single vortex correspond the motion in the orbit

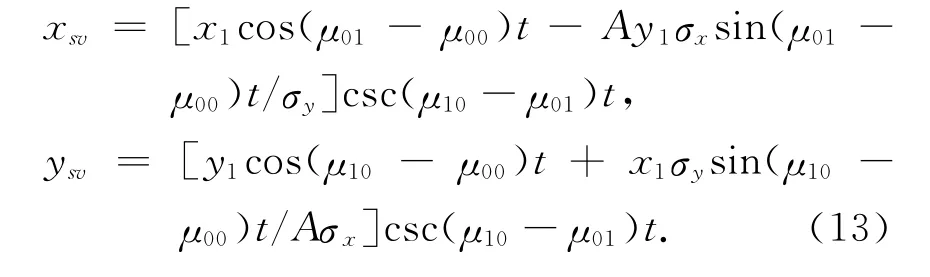
Obviously，whenσx=σythis orbit is an exact circle for A=1，an ellipse for A ≠1，and a more complicated non-closing orbit is obtained whenσx≠σy.

2.2.2 Pair of vortices

A similar solution is obtained for the case of apair of vortices.For the isotropic case，σx=σy=σ，of two vortices with identical topological charges，the wave function is given

2.2.3 Vortex dipole

In the case of a vortex dipole formed by a pair of vortices with opposite topological charges，we have

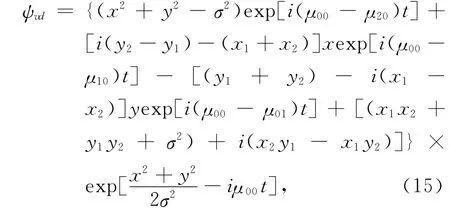
where，（x1，y1）and（x2，y2）are the initial positions that of the two vortices.

In order to check the validity of the analytical solutions（12），（13），（14），presented above，we have also numerically solved Eq.（2）with initial conditionsψsv（x，y，0），ψvp（x，y，0），andψvd（x，y，0）using the time-splitting spectral method，which is explicit，unconditionally stable，and spectrally accurate in space.Plots of the distributions of probability density of the BEC in the 2D space at different instant of time are presented for single vortex，pair of vortices，and vortex dipole in Figs.1（a），（b）and（c），respectively.

In each panel，the plots from top-left to bottom-right correspond to times t=0，0.3927，0.7069，1.0210，1.3352，1.6493，1.9635，and 2.2777，respectively.For the calculation，we have selected a small value of the（weak）g2d=0.1，and set the initial positions at（0.3，0）with A=1 for the single vortex case；at（±0.3，0）with identical topological charges of+1for the pair of vortices case；and at（0.9，0.1）and（-1.1，0）for the vortex dipole case，respectively.As can be observed the vortices can stably exist in all cases for the time evolutions of such non-rotational BEC system.Moreover，they move around the trap center with the shapes keeping approximately unchanged.

Another interesting specific aspect of the vortex motions are the corresponding trajectories.They are shown in Fig.2，where the top，middle and bottom panels correspond to the single vortex，pair of vortices and vortex dipole，respectively.In this figure，the solid lines represent the variational analytical results and the small circles mark the position of the data obtained by numerical integration.As can be seen，in all cases the variational results are in very good agreement with the exactly numerical calculation.Moreover，the single vortex（top panel）moves on a circle when A=1，and on more eccentric ellipses as Adecreases from 0.8，0.6to 0.4.The two vortices in the pair（middle panel）move on deformed circles，although they move independently on each exactly circle for ideal BECg2d=0.Evidently，it is the two-body interactions that cause these two vortices affect each other.For the vortex dipole，the moving orbit is more complicated due to the creation and annihilation of vortex.

3 Chaotic quantum trajectories

Fig.1 Quantum probability density distributions for a BEC in an isotropic trap corresponding to the solutions（12），（13），（14）at time t=0as initial states，and the results are shown as panels（a），（b），（c）for single vortex，vortex pair and vortex dipole，respectively.Here，nonlinear interaction g2d =0.1，the single vortex lies in the position（0.3，0），two vortices with identical topological charge lie in（±0.3，0），and two vortices with opposite topological charge locate at positions of（0.9，0.1），（-1.1，0）initially

Fig.2 Vortex trajectories for the single vortex（left），pair of vortices（middle），and vortex dipole（right）cases discussed in the text.From top to bottom the nonlinear interaction is chosen as 0.1，1，10，and the initial positions of the vortices are the same with that in Fig.1.The solid lines correspond to the variational analytical results and the small cycles represent the data obtained from direct numerical calculations corresponding to Fig.1

In the previous section we have seen how differentsuperfluid velocity fields appear for different vortex aggregations，i.e.single vortex，pair of vortices，and vortex dipole.Accordingly，it should be expected that the corresponding QTs in these fields will exhibit also different characteristics.The aim of the present Section is to carry out a study of the these properties.In order to study the complexity of the QTs，we use a stroboscopic Poincarésurface of section by plotting coordinates xand yat equal time intervals given byt=nT，being T=2π／（μ10-μ00）and nan integer.This is a standard technique in nonlinear dynamics.Some results are shown in Figs.3，4，and 5 for the cases of a single vortex，pair of vortices and vortex dipole described in the previous section，respectively.The procedure used to construct these plots is the following.Thirty initial conditions are chosen randomly，and each of the associated trajectory is followed for 1500crossings with the surface of section.

据全国第二次土壤普查成果，研究区内土壤类型主要有麻石硅铝质粗骨土、麻石黄棕壤和麻沙泥田(图2)，各类型土壤特征如下：

Fig.3 Plot of the Poincarésurface of section for the case of a single vortex.The parameters g2d =0.1，which results inσx=σy=1.00396，A，which determines the shapes of vortex orbits is selected as（a）A=1，（b）A=0.8，（c）A=0.6，and（d）A=0.4，respectively

As can be seen in Fig.3，the results in the one vortex case show that for A =1，where the orbit of the moving vortex is circular［see Fig.2（left）］，all QTs are regular，with a phase space structure organized around two stable and one unstable fixed points that appear in the stroboscopic Poincarémap.As Ais decreased，to 0.8，0.6，and 0.4，and the orbit of the moving vortex becomes more and more elliptic［see Fig.2（left）］，the QTs undergo a transition from to regular to chaotic and increasingly larger bands of stochasticity appear on the corresponding separatrices，as clearly appreciated in Figs.3（b）～（d）.Here，this kind of transition results from a produce of a saddle point，and the associated stable and unstable manifolds interact each other and form a structure of Smale horseshoe chaos band.Therefore，the motion orbits of the vortex have an important influence to the complexity of the corresponding QTs.

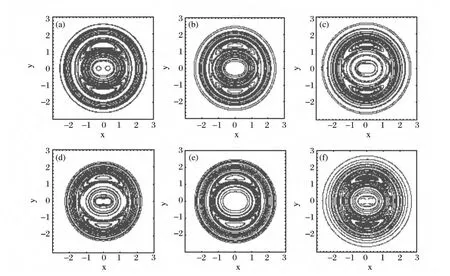
Fig.4 Plot of the Poincarésurface of section for the case of a vortex pair in an isotropic trapping potential.The vortices are initially placed at positions（0.1，1）and（-0.5，-1），respectively.The influence of nonlinear interaction on the onset of chaos：（a）g2d =0，（b）g2d =0.1，（c）g2d =0.5，（d）g2d =0.8，（e）g2d =1，and（f）g2d =1.5，is considered

Now，let us continue and consider the case of apair of vortices studied in the previous section，whose vortex orbits are given by the solution of Eq.（13）.Considering the isotropic trap，λ=1，and choosing the initial positions of the two vortices being located at（-0.3，0），（0.3，0），respectively，the corresponding chemical potentials are given by

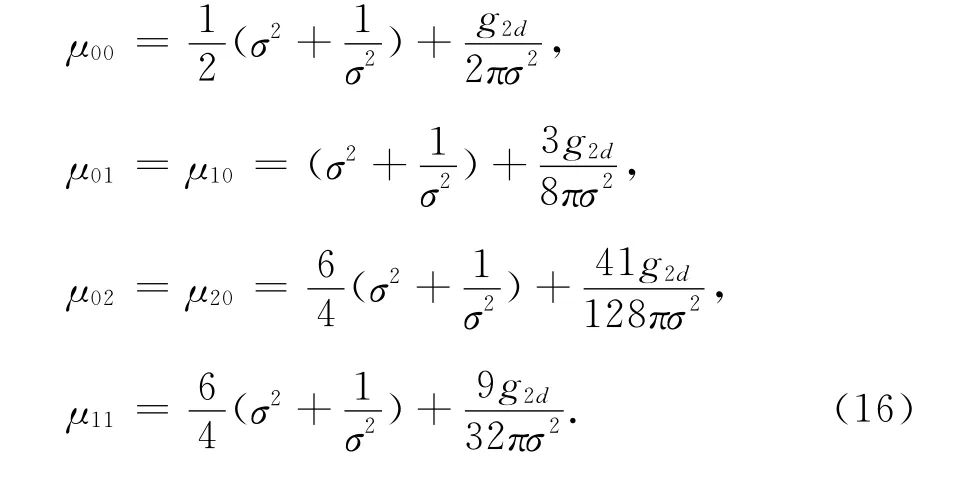
It is evident that for ideal boson gas，where，g2d=0，μ20 =μ02 =μ11，and the solution of Eq.13 can be factorized，with two vortices moving on the circle independently，with a time-periodic velocity field.In this case the regularity of the associated quantity is preserved，as can be seen in Fig.4（a）.However，when considering a（weakly）interacting boson gas with increasingly larger values of g2d，μ11 deviates fromμ02 =μ20 more and more，and the solution cannot be any longer factorized；the two vortices move in a non-periodic orbit，influencing each other simultaneously，as it was given in middle panel of Fig.2.In this case，we find that the periodicity of the velocity field is destroyed due to the fact that the ratio between the two frequenciesω1=μ11-μ00andω2=μ20-μ00is not a rational number any longer.These changes in the moving orbits of the vortices in the pair and the non-periodicity in its time evolution break the regularity of some of the corresponding QTs.This process is shown in the results shown in Figs.4（b）～（f）.

Therefore，in our BEC system theinteratomic interaction plays a key role in the development of complexity of the QTs.It is the interatomic interaction that causes a difference in the couplings between levels ofμ00andμ20and the one betweenμ00 andμ11.Thus，the properties of the superfluid field are determined by the two corresponding time-evolving frequencies.As the interaction becomes stronger，the velocity field deviates more and more from the being periodic，and conse-quently the corresponding Bohmian trajectories become more and more irregular，as clearly seen in Fig.4withT=π／（μ02-μ00）+π／（μ11-μ00）.

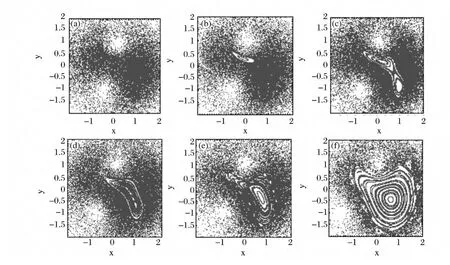
Fig.5 Plots of the Poincarésurface of section for the case of a vortex dipole in isotropic trapping potential.The case of an ideal boson gas，g2d =0，with more and more distance between initial positions of the vortices：（a）（0.1，1），（-0.5，-1）；（b）（0.1，1），（-0.6，-1）；（c）（0.1，1），（-0.7，-1）；（d）（0.1，1），（-0.8，-1）；（e）（0.1，1），（-0.9，-1）；and（f）（0.1，1），（-1.5，-1），is considered

Finally，for the case of a vortex dipole consisting of two vortices with opposite topological charges the situation becomes more complicated.This is due to the fact that annihilation and reappearance of vortices take place.We consider first case of an ideal Bose gas，setting the initial positions of two vortices at（0.1，1）and（-0.5，-1），respectively.Similarly to the analysis carried out previously for a single vortex and a pair of vortices，we consider the stroboscopic Poincarésurfaces of section at the intervals of time given by t=nT，with T =4π［1／（μ01 -μ00）+1／（μ20 -μ00）］／3.The corresponding results are shown in Fig.5（a）.Then，in the other panels，i.e.Fig.5（b）-（f），different initial positions of the vortices，corresponding to an increasing distance between them，are considered.As can be seen，our results show that the original two regular islands observed in the pair of vortices case［Fig.4（a）］change now to a single regular island，whose area in phase space increases with the distance between vortices.This phenomenon is obviously originated by the interaction between the two vortices.

To further analyze this result let us consider next the orbits of the vortices in the dipole for all cases presented in Fig.5.The corresponding results are shown in Fig.6.As can be seen，the overlap between two trajectories becomes smaller and smaller，as the vortex distance increases.This is consistent with the conclusions drawn from Fig.5，since，as this happens，the vortex interaction decreases.This is especially true in the case corresponding to Fig.6（f），where the two vortexes annihilate each other during some period of time.This is obviously consistent，and explains the big growth of the regular island observed in Fig.5（f）.

To conclude this section，let us examine now in more detail how the interatomic interaction in a weakly interacting Bose gas relates to the onset of chaos.Notice that this is similar to what we did in the case of the vortex pair above（see Fig.4）.For this purpose we analyze，as an example，the stroboscopic surfaces of section for the case corresponding to Fig.5（f），that is when the vortices in the dipole are located at positions（0.1，1），（-1.5，-1），respectively，for different values of the interaction parameter g2d=0.005，0.01，0.05，and 0.1.The results are shown in Fig.7.In it，the destruction of regular orbits with the appearance of an associated diffusion in phase space as the nonlinear interaction grows can be quantitatively appreciated.Interesting enough is the appearance of a conspicuous chain of islands around the regular region for the highest values of g2dconsidered.

Fig.6 Plots of the moving orbits of the vortex dipole for each case in Fig.5.

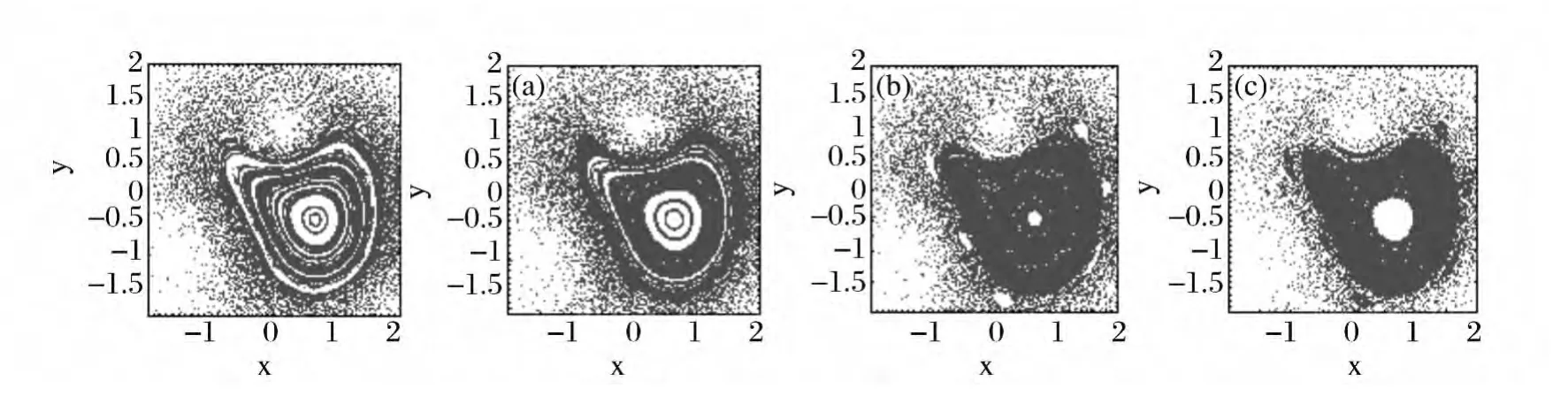
Fig.7 Considering the influence resulted from interatomic interaction，we increase the parameterg2d ：（a）0.005，（b）0.01，（c）0.05，（d）0.1，and redraw the figure in Fig.5（f）.The originally regular island diffuses

4 Conclusion

In summary，different vortex solutions were presented by a variational method.The dynamics of these different vortex clusters in the non-rotating BEC with weakly interatomic interaction were investigated analytically and by direct numerical simulations.Based on the variational vortex solutions，we studied the complexity of the QTs from the Bohmian quantum mechanics point of view.We found the moving orbits of the vortices，interatomic interaction and the interaction between vortices would influence the chaotic properties of the corresponding QTs dominantly.Deformation of single vortex orbit from a circular line to a elliptical one induces the onset of chaos in the Poincarésurface of section of QTs.The interatomic interaction，which destroys the periodicity of the velocity field，also makes the QTs change from regular to irregular.Finally，remoteness between two vortices in vortex dipole induced the growth of the regular island that embedded in the chaotic sea.

［1］ Vilenkin A and Shellard E P S.Cosmic strings and other topological defects［M］.Cambridge：Cambridge University Press，1994.

［2］ Anderson P W，Itoh N.Pulsar glitches and restlessness as a hard superfluidity phenomenon［J］.Nature（London），1975，256：25.

［3］ Blum T，Moore M A.Failure of hydrodynamics within the vortex-liquid phase［J］.Phys.Rev.B，1995，51：15359.

［4］ Swartzlander G A and Law C T.Optical vortex solitons observed in Kerr nonlinear media［J］.Phys.Rev.Lett.，1992，69：2503.

［5］ Madelung E.Quantentheorie in hydrodynamischer form［J］.Z.Phys.，1927，40：322.

［6］ Wyatt R E.Quantum dynamics with trajectories：introduction to quantum hydrodynamics ［M］.New York：Springer，2005.

［7］ Donnelly R J.Quantized vortices in helium Ⅱ［M］.Cambridge：Cambridge University Press，1991.

［8］ Vollhardt D，Wölfle P.The superfuid phase of helium 3［M］.London：Taylor and Francis，1990.

［9］ Parks R D.Superconductivity ［M］.New York：Marcel Dekker，1969.

［10］ Matthews M R，et al.Vortices in a Bose-Einstein condensate ［J］.Phys.Rev.Lett.，1999，83：2498.

［11］ Madison K W，et al.Vortex formation in a stirred Bose-Einstein condensate［J］.Phys.Rev.Lett.，2000，84：806.

［12］ Anderson B P，et al.Vortex precession in Bose-Einstein condensates：observations with filled and empty cores ［J］.Phys.Rev.Lett.，2000，85：2857.

［13］ Abo-Shaeer J R，et al.Observation of vortex lattices in Bose-Einstein condensates ［J］.Science，2001，292：476.

［14］ Coddington I，et al.Observation of Tkachenko oscillations in rapidly rotating Bose-Einstein condensates［J］.Phys.Rev.Lett.，2003，91：100402.

［15］ Mateveenko S I.Vortex structures of rotating Bose-Einstein condensates in an anisotropic harmonic potential［J］.Phys.Rev.A，2010，82：033628.

［16］ Middelkamp S，et al.Bifurcations，stability，and dynamics of multiple matter-wave vortex states［J］.Phys.Rev.A，2010，82：013646.

［17］ Neely T W，et al.Observation of vortex dipoles in an oblate Bose-Einstein condensate［J］.Phys.Rev.Lett.，2010，104：160401.

［18］ Madison K W，et al.Vortices in a stirred Bose-Einstein condensate［J］.J.Mod.Opt.，2000，47：2715.

［19］ Ramman C，et al.Vortex nucleation in a stirred Bose-Einstein condensate［J］.Phys.Rev.Lett.，2001，87：210402.

［20］ Leanhardt A E，et al.Imprinting vortices in a Bose-Einstein condensate using topological phases［J］.Phys.Rev.Lett.，2002，89：190403.

［21］ Klein A，et al.Dynamics of vortices in weakly interacting Bose-Einstein condensates ［J］.Phys.Rev.A，2007，76：043602.

［22］ Crasovan L，et al.Globally linked vortex clusters in trapped wave fields［J］.Phys.Rev.E，2002，66：036612.

［23］ Crasovan L，et al.Stable vortex dipoles in nonrotating Bose-Einstein condensates［J］.Phys.Rev.A，2003，68：063609.

［24］ Möttönen M，et al.Stationary vortex clusters in nonrotating Bose-Einstein condensates［J］.Phys.Rev.A，2005，71：033626.

［25］ PietiläV，et al.Stability and dynamics of vortex clusters in nonrotated Bose-Einstein condensates［J］.Phys.Rev.A，2006，74：023603.

［26］ Schweikhard V，et al.Vortex-lattice dynamics in rotating spinor Bose-Einstein condensates［J］.Phys.Rev.Lett.，2004，93：210403.

［27］ Mueller E J，Ho T L.Two-component Bose-Einstein condensates with a large number of vortices［J］.Phys.Rev.Lett.，2002，88：180403.

［28］ Kasamatsu K，Tsubota M，Ueda M.Vortex phase diagram in rotating two-component Bose-Einstein condensates［J］.Phys.Rev.Lett.，2003，91：150406.

［29］ Choi S J，et al.Dynamics of vortex matter in rotating two-species Bose-Einstein condensates［J］.Phys.Rev.A，2007，75：031604（R）.

［30］ Corro I，et al.Dynamics of two-component Bose-Einstein condensates in rotating traps［J］.Phys Rev.A，2009，80：033609.

［31］ Bohm D.A suggested interpretation of the quantum theory in terms of"hidden"variables.I［J］.Phys.Rev.，1952，85：166.

［32］ von Neumann J.Mathematical foundations of quantum mechanics［M］.Princeton：Princeton University Press，1955.

［33］ Maroney O，Hiley B J.Quantum state teleportation understood through the Bohm interpretation［J］.Found.Phys.，1999，29：1403.

［34］ Dey B K，et al.Alternating direction implicit technique and quantum evolution within the hydrodynamical formulation of Schrodinger＇s equation［J］.Chem.Phys.Lett.，1998，297：247.

［35］ Lopreore C L，Wyatt R E.Quantum wave packet dynamics with trajectories［J］.Phys.Rev.Lett.，1999，82：5190.

［36］ Wyatt R E.Quantum wave packet dynamics with trajectories：application to reactive scattering［J］.J.Chem.Phys.，1999，111：4406.

［37］ Prezhdo O V，Brooksby C.Quantum backreaction through the Bohmian particle ［J］.Phys.Rev.Lett.，2001，86：3215.

［38］ Wisniacki D A，Pujals E R.Motion of vortices implies chaos in Bohmian mechanics［J］.Europhys.Lett.，2005，71：159.

［39］ Wisniacki D A，et al.Vortex interaction，chaos and quantum probabilities［J］.Europhys.Lett.，2006，73：671.

［40］ Wisniacki D A，et al.Vortex dynamics and their interactions in quantum trajectories［J］.J.Phys.A，2007，40：1

［41］ Oriols X.Quantum-trajectory approach to time-dependent transport in mesoscopic systems with electron-electron interactions［J］.Phys.Rev.Lett.，2007，98：066803.

［42］ Englert B G，et al.Surrealistic Bohm trajectories［J］.Z.Naturforsch.，1992，47：1175；Dürr D，et al.Comment on surrealistic Bohm trajectories［J］.Z.Naturforsc.，1993，48：1261；Dewdney C，et al.How late measurements of quantum trajectories can fool a detector［J］.Phys.Lett.A，1993，184：6.

［43］ Frisk H.Properties of the trajectories in Bohmian mechanics［J］.Phys.Lett.A，1997，227：139.

［44］ Wisniacki D A，et al.Dynamics of quantum trajectories in chaotic systems［J］.Europhys.Lett.，2003，64：44.

［45］ Cohen-Tannoudji C，Diu B，Lalo¨eF.Quantum mechanics［M］.New York：Wiley-Interscience，1977.