一维光子晶体能带结构特性分析

李 棚，金宗安，刘明明

六安职业技术学院信息工程系，安徽 六安 237100

1987年，E. Yablonovitch 与S. John根据半导体材料中形成电子能隙的物理机理，提出了在介电材料周期性排列的光子系统中也会出现光子能隙[1] [2]。将介电材料在三维空间进行周期性排列，固定波段的电磁波会因为干涉呈现衰减性传输，色散关系呈现带状，此种现象称为光子晶体带隙[3] [4]。相对于三维、二维的复杂结构，两种介电材料周期性堆叠在一起形成的一维光子晶体，具有结构简单，计算方便，便于制作的优势，受到众多科研工作者的重视[4] [5]。通过理论分析发现，一维光子晶体结构满足一定的条件，能够实现全向反射光子禁带。

1 一维光子晶体理论模型

虽然光子与电子之间存在诸多相似之处[6]，但是，由于光子之间不存在库仑作用，两者之间的理论分析还有不可忽视的差异。现阶段主要采用平面波展开法[7](PWM)，传输矩阵法[8] [9](TMM)，时域差分法[10](FDTD)等方法分析一维光子晶体。其中平面波展开法是光子晶体计算方法中应用最早，最为广泛的一种方法。它综合使用了薄膜光学的传输矩阵理论和固体物理的Bloch定理，解释了光子带隙的形成机理，相对于其他研究方法，物理意义更清晰、更深刻。本文将利用平面波展开法，计算一维光子晶体的色散曲线，找出其能隙位置，分析能隙特点，判断全向带隙的充分必要条件。

(1)

(2)

(3)

2 光子带隙数值分析

设一维光子晶体由A、B两种薄膜沿着x方向交替组成。如图1(a)所示，A、B膜层的表面平行于y-z平面。A、B的折射率分别为nA和nB,厚度分别为dA和dB。光波在xy平面内传播，如图1(b)所示，从空气介质中入射λ0光波，在第α(α=A,B)种材料中的波长计算为λa=λ0/na，波矢的切向分量为β=kay=kasinθα/λ0，由折射定律可知，nasinθa保持不变，故ky是一个常数。当电磁波以角度θ0入射并在该光子晶体中传输时满足Bloch定理，电场的数学表达式为

EK(x,y)=EK(x)eiKxeiKy

(4)

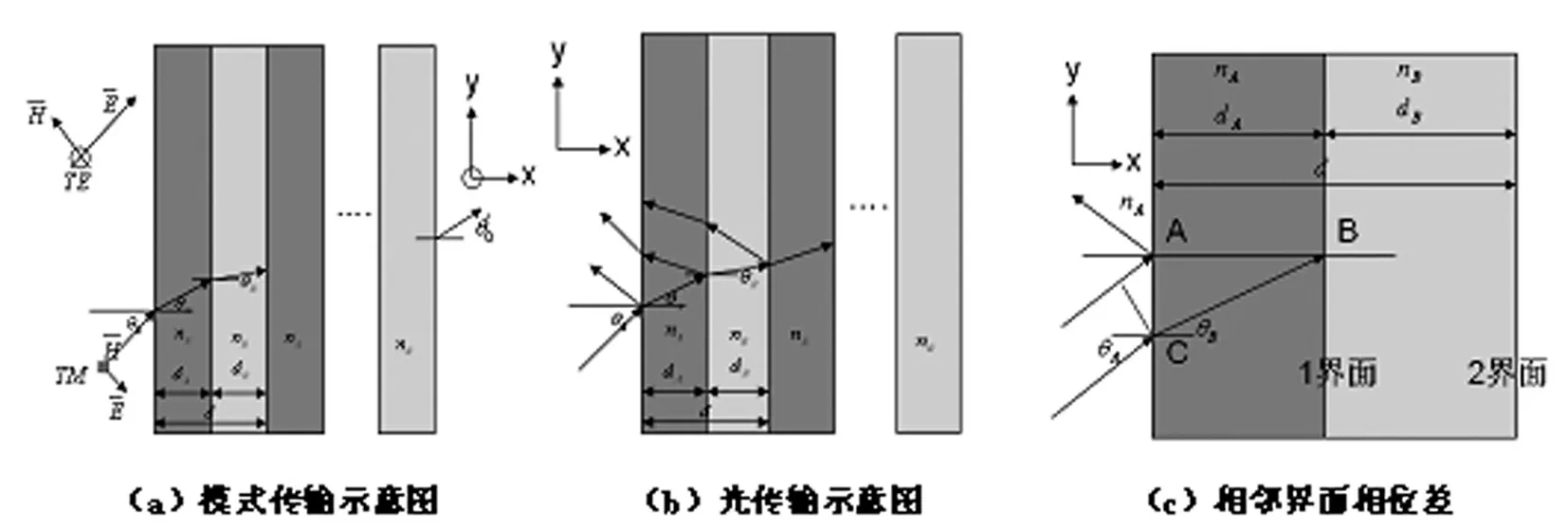
图1 周期性一维光子晶体结构示意图

考虑光子晶体的一个晶格常数中光的相位关系，如图1(c)，其中入射角为θA，折射角为θB的光在相同y坐标的A与B两点的位相差δ。C点超前于A点的位相为2πdtgθBsinθA/λA，B点滞后于C点的位相为2πd/(λAcosθB)，所以A点超前于B的相位

δ=2πd/(λBcosθB)-2πdtgθBsinθA/λA=2πd(1-nAsinθB/nB)2πdcosθB/λB=k2xd

其中k2x表示材料B中波矢的垂直分量，后续公式中的k1x表示材料A中波矢的垂直分量。考虑分界面上的电磁场的切向分量，An-1表示从A1介质入射的电场强度切向分量，Bn-1表示从B1介质反射的电场强度切向分量；Cn表示从B1介质入射的电场强度切向分量，Dn表示从A2介质反射的电场强度切向分量；An从A2介质入射波电场强度的切向分量，Bn表示从B2介质反射的电场强度切向分量。

E和H切向分量在1界面两侧连续：

An-1+Bn-1=exp(ik2xdA)CN+exp(-ik2xdB)Dn
k1z(An-1-Bn-1)=k2z[exp(ik2xdB)Cn-exp(-ik2xdB)Dn]

(5)

同比的，在界面2左右两侧有

Cn+Dn=exp(ik1xdA)An+exp(-ik1xdA)Bn
k1z(Cn-Dn)=k1z[exp(ik1xdA)An-exp(-ik1xdA)Bn]

(6)

由上面四式，可推得

(7)

其中，

(8)

由于一维光子晶体结构满足周期性结构，因此光波在系统中满足Bloch条件：

(9)

将式(9)与式(7)联立求方程可以得到：

(10)

通过(10)式可以判断光子晶体带隙的位置，以及传输状态。对于导带具体细节可以在另一篇论文中介绍。因此，满足(1/2)(A+D)>1条件， Bloch波矢是复数，Bloch波矢衰减的，这些区域称为禁带或光子带隙；满足(1/2)(A+D)<1条件，Bloch波矢是实数，光允许在系统中传播，对应的区域称为允带；满足(1/2)(A+D)=1条件为能带边缘，为了获得光子晶体能带特性，只需求得能带边缘位置就可以了。

对于TM偏振，将上述计算流程中将电场换成磁场便可以获得TM偏振。即将(8)式中的系数改为如下内容，最终的判断条件不变。

(11)

3 数值计算结果及分析

取一维光子晶体结构参数一为nA=4.6,nB=1.6,dA=0.33d,dB=0.67d，绘制如图(2)的光子晶体带隙结构。取一维光子晶体结构参数二为nA=2.2nB=1.7，dA=0.33d，dB=0.67d，绘制如图(3)光子晶体带隙结构，彩色区域为光子晶体中传输态，蓝色区域为光子晶体的消逝态。

图2 高折射率差光子晶体能带结构图

图2(a)为结构参数一的TE模式能带图，图2(b)为结构参数一的TM模式能带图，通过两图的能带比较可以发现，在归一化频率范围内的光子带隙数量相同，拥有5个带隙，其中频率最低的带隙(第一带隙)最宽。其中，随着切向波矢分量的增大(入射角度的增大)TE模拟和TM模式的带隙都在向高频方向移动。同时，TE模式的带宽展宽，TM模式的带宽收缩。

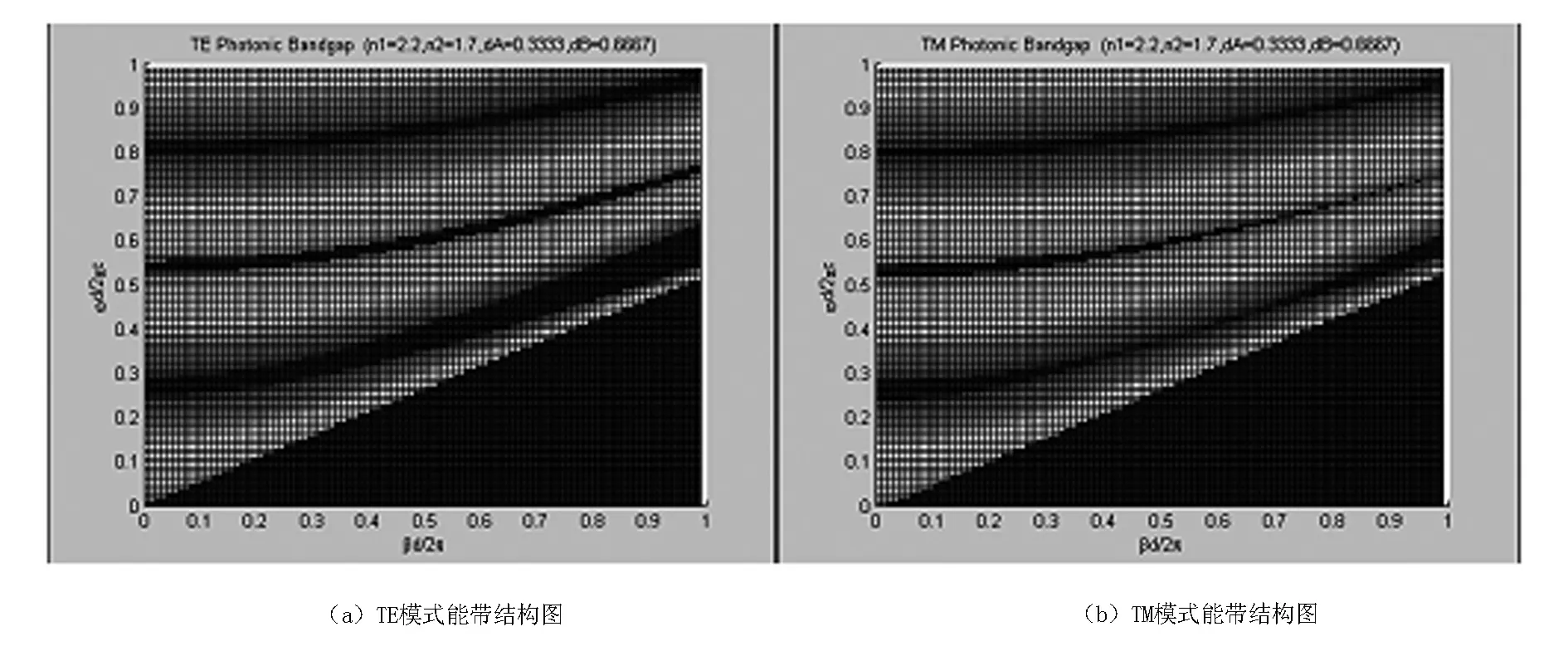
图3 较低折射率差光子晶体能带结构图

图3(a)为结构参数二的TE模式能带图，图3(b)为结构参数二的TM模式能带图，通过两图的能带比较发现，在归一化频率范围内的光子带隙数量也是相同的，拥有3个带隙，其中频率最低的带隙(第一带隙)最宽。随着切向波矢分量的增大(入射角度的增大)TE模式和TM模式的带隙都在向高频方向移动。同时，TE模式的带宽展宽，TM模式的带宽收缩。相比较图2与图3，可以发现，在增大两种介质折射率差值时，会增加光子带隙数量，带隙中心频率向低频方向移动，同时增大带隙宽度。

一维光子晶体的全向反射是指一维光子晶体能够对从垂直入射到掠入射全角度范围内的某频率范围的TE模式和TM模式都具有很高的反射率，该频率范围为全向反射带。下面，通过分析结构参数一能带结构中的第一带隙，介绍一维光子晶体实现全向反射的充分和必要条件。TE模式的第一带隙如图4，TM模式的第一带隙如图5。

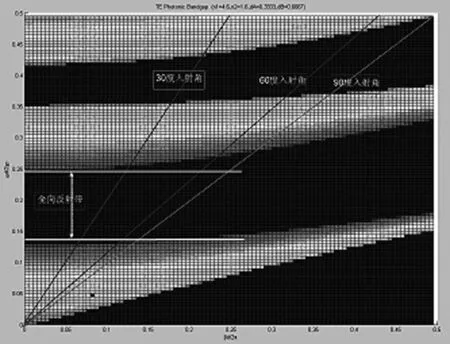
图4 TE模式全向反射带隙条件判定

不同入射角θα的光具有不同的切向波矢分量β=kay=kasinθα/λ0，由图4可知，红色线为90°掠入射光线，光线只有在掠入射光线以上区域方可传输到光子晶体内部。两根蓝色的线分别为30°入射角和60°入射角线，纵坐标为垂直入射光线，即入射角为0°。要实现TE模的0°到60°的反射，必须是在白色实线之间的频率方可。

图5 TM模式全向反射带隙条件判定

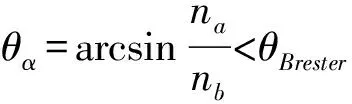
4 小结

在众多的一维光子晶体分析方法中，平面波展开法是在不考虑复杂情况下，能够较准确的分析一维光子晶体带隙的一种方法。在归一化频率范围内能够出现多个带隙，其中，介质折射率之差影响带隙数量，带隙宽度，带隙中心频率。另外，布儒斯特角的大小直接关系到全向反射的可能性。对于光子晶体介质参数对带隙的影响，以及入射光线的透射率和反射率以及色散问题，将采用传输矩阵法进行分析，另文研究[11]。

[1] Yablonowitch E Inhibited spontaneous emission solid-state physics and electronics [J]. Phys Rev Lett,1987,58 (20):2059-2061

[2] Joannopoulos J D, Meade RD, Winn JN. Photonic crystal: Molding the flow of light[M].Princeton: Princeton University Press,1995

[3] 李 棚,张明存,叶 飞.一维光子晶体全向带隙限光特性的研究[J].井冈山大学学报(自然科学版),2012,33(3):26-30

[4] 张 玲,梁 良,张琳丽,等.一维光子晶体带隙结构研究[J].光子学报,2008,37(9):1815-1818

[5] 陈慰宗，忽满利，李绍雄，等．一维光子晶体禁带的特点及增宽[J]．西北大学学报：自然科学版，2002，32(6)：625-628

[6] 刘思科，朱秉升，罗普生，等.半导体物理学[M].北京：电子工业出版社，2003

[7] 段晓峰，牛燕雄． 一维光子晶体的光学传输特性分析[J]． 光子学报，2003，32( 9) : 1086-1089

[8] 刘鸿娟, 叶志清, 邓海东, 等. 用转移矩阵方法计算一维光子晶体的禁带结构[J]. 江西师范大学学报:自然科学版, 2004, 28(2) :105-108

[9] 王 辉，李永平．用特征矩阵法计算光子晶体的带隙结构[J]．物理学报，2001，50(11)：2172-2178

[10] 葛德彪，闫玉波.电磁波时域有限差分法[M].西安：西安电子科技大学出版社，2005

[11] 李 棚,张明存,叶 飞. 一维光子晶体周期层厚度对禁带宽度的影响[J].赤峰学院学报(自然科学版),2012(6):81-82