非对称3-(2SPS)并联机床的灵巧度分析
2014-03-17陈婕李开明
陈婕,李开明
(南京理工大学机械工程学院,江苏南京210094)
并联机床是以空间并联机构为基础的新一代加工设备,它是基于机床技术、机器人技术和现代数控技术相结合而出现的新型机床[1]。自20世纪90年代中期出现以来,已引起了越来越多的专家和学者的关注。并联机床的灵巧度反映了关节动作向操作动作的映射能力,是度量机床在加工过程中动力学性能的主要指标,也是确定刀具位置的关键因素[2],因此灵巧度的研究对于并联机床的设计和实用性具有重要意义。
SALISBURY 等人提出采用逆雅可比矩阵的最大与最小奇异值的比值即逆雅可比矩阵的条件数来衡量并联机床的灵巧度。文中对3-(2SPS)并联机床的灵巧度进行了研究,利用MATLAB 分析了灵巧度在工作空间的变化规律。
1 3-(2SPS)并联机床机床描述
图1所示为3-(2SPS)并联机床的结构简图。该机床由3 组平行驱动杆(A1a1//A2a23、A3a23//A4a45、A5a45//A6a6)、动平台(a1a23a45a6)以及定平台(A1A2A5A6)组成。平行杆两端与上下平台之间采用球铰链铰接,杆组A1a1、A2a23、A5a45、A6a6在同一平面A1A2A5A6内,铰接点A3、A4与平面A1A2A5A6的距离为u。3 组平行杆由伺服电机同步驱动,以改变动平台在一定空间内的位置和姿态。动平台a1a23a45a6为等腰梯形,上底和腰长为d,底角为β。定平台铰接点安装距离为d,即A1A2= A3A4= A5A6=a1a23=a23a45=a45a6=d。
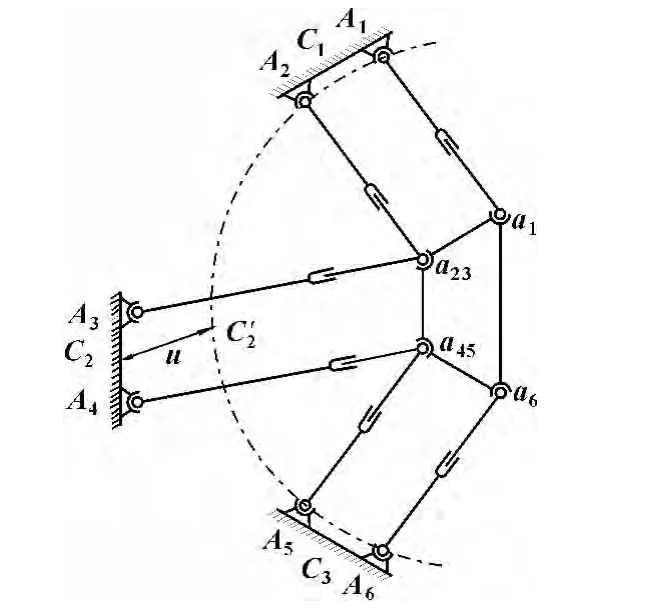
图1 3-(2SPS)并联机床结构简图
2 逆雅可比矩阵
逆雅可比(Jacobin)矩阵反映了关节空间速度与末端操作器速度的映射关系,也称为一阶运动影响系数。求解逆雅可比矩阵是分析机床性能的基本要求。
如图2所示,C1、C2、C3分别是A1A2、A3A4、A5A6的中点,C'2是C2在A1A2A5A6平面内的投影,三角形C1C'2C3为等腰直角三角形,其外接圆圆心为O,半径为R。在定平台上以O 为原点建立直角坐标系O-xyz,z 轴沿OC1方向,y 轴在A1A2A5A6平面内且垂直于z 轴,x 轴方向由右手定则判定。动平台上以a1a6的中点O'为原点建立动坐标系O'-x'y'z',z'轴沿O'a1方向,y'轴在a1a23a45a6平面内且垂直于z'轴,x'轴方向由右手定则判定。
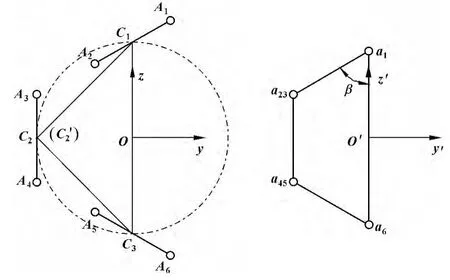
图2 定、动平台铰链点几何关系
四边形a1a23a45a6的边a1a6的中点为O'。β =30°,偏置u = 500 mm,O'相对于定平台的坐标为(x,y,z),得机床的位姿反解方程为:
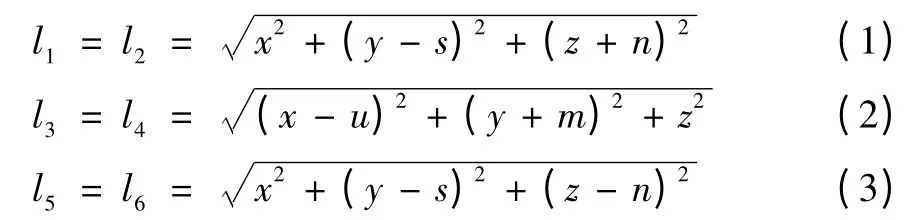
其中:li为伸缩杆的长度,i=1,2,…,6;
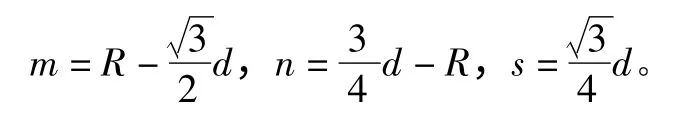
伺服电机驱动两根平行杆同步伸缩,所以该机床只能沿着x、y、z 3 个坐标轴平动,而不能绕着3 个坐标轴转动,其逆雅可比矩阵的公式如式(4)所示:

由式(1)—(4)得:

由公式可以看出逆Jacobin 矩阵与机床的实际操作速度无关,只和机床的尺寸参数和位形有关[3],基于这个特点,该矩阵对机床的灵巧度研究有很大的帮助。
3 灵巧度分析
灵巧度是衡量操作空间随着关节空间变化而变化的敏感度。灵巧度有3 个度量指标[4]:逆Jacobin 矩阵的条件数、最小奇异值和可操作性,分别反映机床的各向同性、响应速度和可操作性。一般情况下,各向同性最能体现机床的灵巧度规律,文中在此只对机床的各向同性进行研究。
操作空间速度向关节空间映射时存在如式(6)所示的关系:

式中:v 是关节输入速度,u 是末端操作手的速度。
由式(6)可得:

由矩阵的相容性可知:

实际控制过程中在工作空间内,雅可比矩阵J 是可逆的,则同式(8)得:
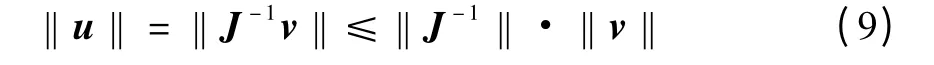
由式(8)、式(9)可得:

这里采用矩阵的谱范数得出雅可比矩阵的条件数m,令m=‖J‖·‖J-1‖=n1/n2,n1、n2分别为逆雅可比矩阵的最大、最小特征值。可以看出:当条件数大,则u 微小变化将引起v 较大的变化,即机床稳定性差;当条件数小,则u 有微小的变化,v 变化也很小,此时系统的稳定性好。由条件数的定义可知,条件数变化范围是1 到正无穷,所以当m =1时,系统的稳定性最好。当机床出现奇异位形时,条件数为无穷,这时v 处于失控的状态,即使u 不改变,v 也可能改变。在控制的过程中,不仅要保证机床有较好的灵巧度,同时也要避免奇异位形的出现。
4 仿真分析
给定杆间距d =350 mm,三角形C1C2C3的外接圆半径R = 620 mm,驱动杆的长度变化范围li=650 ~1 200 mm,下面将采用MATLAB 取稍大于工件空间的矩形区域进行仿真,得出不同截面下3-(2SPS)并联机床的条件数即各向同性度uzf 的变化曲线,其中-500 mm≤x ≤500 mm、0 ≤y ≤500 mm、-500 mm≤z≤500 mm。由于仿真空间并没有排除可能出现奇异位形的空间,仿真出的曲线有条件数为0 的情况,不利于曲线的分析,所以采用条件数的倒数进行仿真,其变化范围是0 到1。
从图3(a)可知:在y =350 mm 处,逆雅可比矩阵的特征值出现为0 的情况。图3(b)表明,机床的各向同性度变化比较平缓。对比图3(c)和图3(d)可知:y 增大时,出现奇异位形的位置朝着x 轴的负方向移动。由图3(e)和图3(f)可知:虽然z变化,但是出现奇异位形的位置没有改变,随着z 的增加,各向同性度在整体上增加了,运动精度提高。总体而言,当3 组平行杆处于同一平面时,机床会出现奇异位形,离奇异位形越近的区域,灵巧度越差,在后续的控制中,应该有效地避开这样的位置。
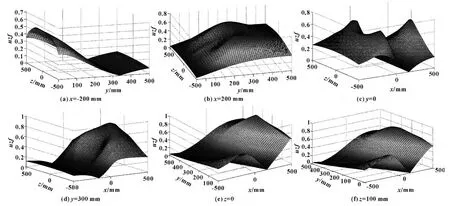
图3 各截面各向同性度的分布
5 结论
通过仿真得出了该并联机床各向同性度的分布规律,也反映出机床可能出现奇异位形的区域。在具体工作时,应控制刀具在灵巧度较好的工作空间中运动,并且进行机床工件坐标系定位时,也可以根据灵巧度的分布情况将工件放置在理想的位置。同时可以对该机床的尺寸参数作进一步的优化,使机床具有最佳的传动性能。
【1】李长河,蔡光起.并联机床发展与国内外研究现状[J].青岛理工大学学报,2008,29(1):7-13.
【2】黄田,汪劲松.Stewart 并联机器人局部灵活度与各向同性条件解析[J].机械工程学报,1999,35(5):41-46.
【3】黄真,赵永生,赵铁石.高等空间机床学[M].北京:高等教育出版社,2006.
【4】陈修龙,赵永生,鹿玲.并联机床的灵巧度评价指标及其应用[J].光学精密工程,2007,15(2):237-242.
【5】李铁民,郑浩峻,汪劲松,等.并联机床不同位形下的运动精度评价指标[J].机械工程学报,2002,38(9):101-105.
【6】王瑜.5-UPS/PRPU 并联机床工件定位系统的开发[D].秦皇岛:燕山大学,2005.
