基于相位差变化率的单站目标定位研究

(中国电子科技集团公司第三十八研究所,安徽合肥230088)

0 引言

无源定位技术是电子对抗应用中的一项重要技术。由于该技术具有作用距离远、隐蔽接收、不易被对方发觉的优点,使得它对于提高系统在电子战环境下的生存能力和作战能力有着重要的作用[1-2]。单站无源定位技术是只利用一个观测平台对目标进行无源定位的技术。由于所能获取的信息量相对较少,单站无源定位实现难度相对较大。其定位实现过程通常是：用单个运动观测站对辐射源进行连续测量,在获得一定量定位信息积累的基础上,进行适当的数据处理以获取辐射源目标的定位数据。从几何意义上来说就是用多个定位曲线(面)的交会来实现定位,即利用运动学原理测距,以振幅、相位或多普勒频率法测向,依靠几何学原理定位,结合非线性滤波技术,实现单站对固定目标的快速高精度无源定位[3-4]。目前,传统的单站无源定位技术研究主要集中在固定单站对机动目标的定位和运动单站对固定目标的定位这两个方面。

本文主要针对运动单站对固定目标基于相位差变化率的定位问题进行展开,主要讨论在测量目标信号入射角及目标信号的相位差的情况下,结合运动平台自身位置及航向等信息对固定目标进行定位,以及如何通过对多次定位进行IMM融合滤波提高目标综合定位精度的问题。着重阐述了基于一维卡尔曼滤波的相位差变化率计算模型、目标定位解算方法及基于IMM滤波的融合滤波定位方法,有效地提高了定位精度。仿真实验中,分析了目标定位的各个过程效果及综合定位性能,最后给出一些工程性建议。

1 定位算法

1.1 定位原理

假设观测平台与辐射源之间进行非径向、匀速直线运动,我们建立一个平面坐标系,如图1所示。图中,V为观测平台速度矢量,R为观测平台至辐射源的水平距离,R0为观测航路捷径,θ为信号入射角。

图1 相位差变化率定位原理示意图

假设观测平台起始信号入射角为θ0,在X轴上的起始坐标x0,运行时间t后的入射角为θ,在X轴上的坐标为x,由几何关系可知

式(1)表明在观测平台飞行过程中,信号入射角θ是速度V、捷径R0及时间t的函数。假设观测平台作匀速直线飞行,则V不变,R0不变,将式(1)对t求导,写成微分形式如下：

如图2所示,如果测量设备基线长度为D,信号频率为f,信号波长为λ,运动平台上两个天线A1和A2接收的信号相位差为

式中,ω为信号角频率,Δt为信号到达A1和A2两个天线阵元的时间差,c为电磁波的传播速度,且假设D远小于运动平台到辐射源之间的距离。

图2 相位差示意图

对式(4)求导后可得相位差变化率为

进而得到

将式(6)代入到式(3)中,可得

从式(7)可以看出,如果能同时测出目标信号入射角θ、相位差变化率̇φ,则可以计算出目标的距离,再结合平台自身的经纬位置坐标和航向信息,就能够解算出目标的绝对坐标位置,实现瞬时定位。

1.2 参数计算

从1.1节中式(7)可以看出,对于目标的定位精度而言,最为关键的是目标信号入射角和相位差变化率的测量精度。在实际的工程中,虽然目标信号的入射角和相位差可以直接测量得到,但由于测量存在较大的量测误差,不能直接通过差分得到相位差变化率,因此首先需要对各个测量参数进行滤波处理。

考虑观测平台的运动轨迹为匀速直线运动,那么对于目标而言,在一个很短的时间内,目标信号的入射角及相位差可以近似看成是线性变化的,由此可以直接应用Kalman滤波器进行滤波处理,考虑参数变化符合匀加速模型(CA),则该模型的Kalman滤波器状态方程和量测方程如下：

参数状态模型

参数量测模型

状态向为X mk=[x,̇x,¨x],状 态 转 移 矩 阵,过程噪声矩阵Gm=[T2/2,T,1]′,量测矩阵H=[100]。

根据Kalman滤波器原理,进行如下递推计算：

将测量的目标信号入射角及相位差代入上述Kalman滤波器,可以得到滤波后的目标信号入射角和相位差变化率。然后,直接代入式(7)即可得到目标的瞬时距离,实现单次目标定位。

2 融合滤波定位

由于在实际测量设备的测量过程中测量误差具有随机性,虽然可以通过上述一维Kalman滤波降低量测误差,但单次目标定位的精度仍然不高。考虑到运动平台对目标的观测通常可以持续一段时间,由此可以利用滤波器将目标的定位结果序列进行融合滤波,从而进一步提高目标定位的精度。

由于目标位置是固定的,不随时间变化,而观测平台自身是线性运动的。因此,根据运动的相对性,可以将观测平台自身的位置看作是固定不变的,将目标看成是相对于观测平台作线性运动。这样可以将单次对目标的定位看成是目标点迹,将提高目标定位精度问题转化为目标点迹的航迹滤波问题。这样,采用交互式多模滤波模型(IM M)对目标点迹进行滤波,则滤波后的目标航迹就是目标相对于观测平台的位置,再结合观测平台自身的位置坐标和航向信息,最终求得目标的绝对坐标位置。

下面考虑对单次定位获得的目标距离方位进行IMM滤波处理。IMM是一种混合系统状态估计的次优算法[5-6]。在时刻k,利用交互式多模型方法进行目标状态估计的计算时,考虑每个模型滤波器都有可能成为当前有效的系统模型滤波器,每个滤波器的初始条件都是基于前一时刻各条件模型滤波的结果的合成。考虑到目标的运动特征,这里主要采用常速度模型(CV)、常加速度模型(CA)和Singer模型作为交互多模的模型集,IM M算法结构如图3所示。

图3 IM M算法结构图

算法的主要步骤为：

第一步 模型条件初始化。

① 计算混合概率

式中,πi,j为假定的马尔可夫模型转移概率,给出了k-1时刻由模型M ik-1到k时刻由模型M jk-1的转移概率,μik-1为k-1时刻的模型M ik-1的概率,其中

第二步 对各模型分别进行卡尔曼滤波。

①预测

②更新

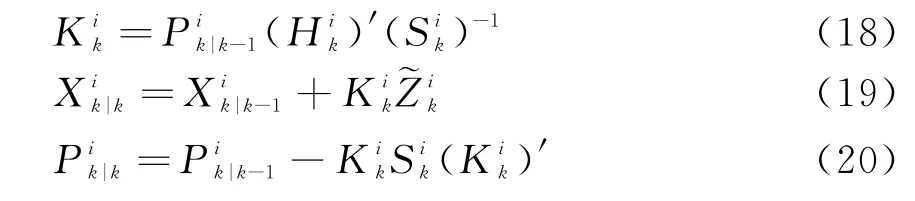
③ 计算模型似然函数。

第三步 模型概率更新。

式中,c为归一化常数。

式中,Λik为在Gauss条件下的似然函数。

第四步 状态估计融合。

计算k时刻,系统融合后的状态和误差协方差阵：

滤波器的输出是多个滤波器估计结果的加权平均值,实现对目标位置的滤波。

3 仿真实验

实验中采用STK-8仿真软件来生成观测平台的运动数据和目标的位置数据及可见性数据,然后通过Matlab(2009a)软件进行算法仿真分析。STK中主要对辐射源目标的截距和位置、观测平台的线路、运动速度、航向、传感器范围等参数进行设置,还包括对仿真时间步长及数据采样率等参数的设定。

3.1 仿真条件

STK仿真实验场景中设定观测平台为机载平台,飞行线路为直线,起始点与终止点经纬坐标分别为(112.890 2E,27.941 9N)和(117.748 5E,34.863 2N),全程899.2 km,飞行速度为200 m/s,飞行高度为8 km。传感器方位可见视角区间为30～150°,俯仰可见视角在[-90°,-3°]范围之内,传感器最大探测距离为230 km,观测时间步长为1 s,参数测量的采样率为20 Hz,仿真总时长为75 min,目标信号入射角测量误差均方根为1°,相位差测量误差均方根为16°,所有测量误差服从高斯分布。地面设定3个海拔高度为0 km的辐射源目标。目标1的经纬坐标为(114.706 4E,29.247 6N),截距81.023 km;目标2的经纬坐标为(115.878 8E,29.572 4N),截距160.235 km;目标3的经纬坐标为(116.916 5E,30.158 6N),截距213.033 km。利用STK软件生成载机飞行位置数据和目标可见性数据,STK仿真场景如图4所示。

图4 STK中仿真场景设置

3.2 数据分析

(1)参数滤波

对于机载侦察设备测量得到的目标瞬时信号入射角和相位差值进行卡尔曼滤波后,可得到目标精确的信号入射角和相位差变化率,图5和图6分别为信号入射角滤波效果图和相位差滤波效果图。

(2)单次定位

根据前面第1节的算法描述,在对目标信号的入射角和相位差进行Kalman滤波后,获得较为精确的信号入射角和相位差变化率,通过式(7)可以得出目标单次定位的位置,单次定位的位置偏差如图7所示。

图5 对目标信号入射角进行Kalman滤波效果图

图6 对目标相位差进行Kalman滤波效果图

图7 目标单次定位偏差曲线

(3)融合定位

接下来,将单次定位的结果进行融合滤波,得到融合定位的结果,再对融合定位结果计算几何平均值作为目标的最终定位结果,如图8所示。

图8 目标融合定位结果图

经过500次蒙特卡洛定位实验,并统计地面3个辐射源目标定位结果,最终对3个辐射源的目标定位结果如表1所示。

表1 三批辐射源目标融合定位结果

3.3 实验结论

经过上述实验结果,可以得出以下几点适用于工程应用的结论：

① 从图5和图6可以看出,在计算目标距离前,采用Kalman滤波模型对目标信号入射角及目标相位差进行滤波,可以有效地降低量测噪声对定位解算的影响。

② 从图7可以看出,对于目标的单次定位,单次定位偏差的均方根在5 km左右,误差仍然较大,需要采用后续的IMM滤波模型进行融合滤波处理。

③ 从图8可以看出,通过假定目标的相对运动,采用CV、CA及Singer运动模型的交互多模滤波,对目标距离、方位进行融合滤波处理,可以有效地降低单次的定位偏差,提高目标定位精度,最终获得较为理想的目标定位效果。

④ 从表1可以看出,对于实验中3个辐射源目标的定位结果均达到CEP误差小于3%的定位精度,验证了本文算法的有效性和定位性能。

4 结束语

本文针对基于相位差变化率的单站目标定位问题展开讨论,给出了量测参数的滤波模型,并在单次定位基础上采用IMM融合滤波定位模型有效地提高了定位精度。仿真实验中,给出了目标参数滤波的效果、目标单次定位的情况以及IMM融合滤波定位的情况,从定位偏差及定位CEP两方面分析了算法的有效性和性能。最后,基于仿真实验的结果分析,给出了一些应用性的实验结论和建议,对工程实践有着重要的参考价值。

[1]胡来招.无源定位[M].北京：国防工业出版社,2004.

[2]王本才,张国毅,侯慧群.无源定位技术研究[J].舰船电子对抗,2006,29(6)：20-26.

[3]李炳荣,曲长文,苏峰.机载单站无源定位技术分析[J].战术导弹技术,2005,27(6)：35-39.

[4]平殿发,司文健,苏峰.基于观测站机动的机载单站无源定位跟踪研究[J].雷达科学与技术,2010,8(6)：499-502.PING Dian-fa,SI Wen-jian,SU Feng.Research on Airborne SOPLAT Based on Maneuvering Observer[J].Radar Science and Technology,2010,8(6)：499-502.(in Chinese)

[5]BLACKMAN S.Design and Analysis of Modern Tracking Systems[M].Norwood,MA：Artech House,1999.

[6]FARINA A,DEL GAUDIO M G,D’ELIA U,et al.Detection and Tracking of Ballistic Target[C]//2004 IEEE Radar Conference,Philadelphia,USA：IEEE,2004：450-456.