基于Kharkov法的单站雷电定位技术研究

何伟峰++陈伟++朱江

摘 要：我国地理环境复杂，使得多站定位网的布设难度加大。采用Kharkov方法进行了单站雷电定位，对距离分别为1 000 km和1 500 km模拟得到的2次雷电波，在时域中对电磁场分量进行了积分处理，获得了坡印廷矢量进行定向。以用频段为1.8～3.5 kHz的一阶相位谱和波导模型计算得到的相位谱进行最小二乘法匹配，获得雷电源的距离。结果表明，通过假定的雷电源方位和由坡印廷矢量计算得到的方位两者之间的差异较小，平均值为2.4°；通过一阶相位谱和在最小二乘法匹配得到的距离处用波导模型计算得到的相位谱的误差较小，可以很好地对雷电发生的距离进行计算。

关键词：雷电定位；单站；坡印廷矢量；相位谱

中图分类号：P427.32 文献标识码：A DOI：10.15913/j.cnki.kjycx.2017.01.086

随着经济的发展和高科技设备的应用，雷电引起的灾害更加常见，后果也更加严重。军事、民用部门等重要的单位对雷电的监测预警有更高的关注度和要求——能通过专门的仪器对雷电的生成、发展走向进行了解，从而得到雷电的实时预警信息。雷电定位系统的必要性和重要性不言而喻，除了能为科研机构提供研究数据，且其定位系统能实时监测雷暴活动的发展情况，获得雷电发生的时空分布、强度等特征量，并提供雷电预警信息，从而减少雷击造成的损失。

20世纪70年代初期，Few利用雷声信号到达不同测站的时间差来进行雷电定位，率先进行了声学定位的实验。在这次研究中，利用4个测站来进行声学信号的接收，并组成了Y形网络；都百万提出使用光电检测技术来进行雷电定位，该系统首先利用探测仪器获得的光感强度进行均化，求得了光信号的方位，并根据声学与光学信号之间的时刻差得到了距离；Burke等人使用ELF频段（5～50 Hz）的3個电磁场分量来构建坡印廷矢量，从而进行定位；李蕾对我国的XDD01型雷电探测系统进行了修正，对80 km外的雷电源均采用了这种方法估算距离，由于其测距精度高、探测范围大，很多单站雷电定位系统都采用该方法。

单站定位具有独特的优势，比如移动的船舰上安装单站雷电定位系统可有效监测雷暴活动情况，以降低遭受雷击的可能性。部队导弹的车载机动发射要求需要单站定位系统提供雷电监测预报，从而保证导弹不受雷击的影响。飞机舱内采取安装单站雷电定位系统来降低航空事故的发生率等。除上述军用方面的应用外，地理环境复杂的山区和岛屿雷电活动频繁，且其布站会受到安装环境的制约，多站定位网无法布设。而单站定位系统凭借其布站灵活、架设方便的优势，弥补了多站定位系统的不足，能有效地监测当地雷暴活动并及时预警，同时，也能获得大量雷电监测数据，为今后的科学研究工作打下基础。

1 Kharkov方法

1.1 Poynting定向（TPDF技术）

1995年，Rafalsky等人提出关于ELF/VLF频段的雷电在宽频带中对3个场分量（水平磁场Hx，Hy和垂直电场Ez）进行时域处理，即TPDF技术，由此得到雷电源对测站的方位。具体的过程如下。

给出频域的坡印廷矢量表达式：

式（1）中：E（ω）和H（ω）分别为电场和磁场通过傅里叶变换得到的频域；* 为复共轭。

定义一个新的全频段的坡印廷矢量∏，其大小是雷电波的能流密度，方向是能流的平均方向，公式如下：

1.2 一阶相位谱定距

将地球-电离层波导假想为理想可导的平面板，雷电源视为r脉冲信号，则无论对于TE波（横电波），还是TM波（横磁波），其n阶模态的相位公式均如下：

式（3）中：krsn为波矢量的水平分量，sn=[1-（nπ/kh）2]1/2，k=2πf/c；r为雷电源与观测点之间的距离；h为地球-电离层波导的高度。

值得注意的是，当频率f超过波导系统的n阶截止频率fn=nc/2h时，sn为实数，即电磁波在波导中不会被截止或衰减，进而在波导系统中正常传播。

2 单站闪电定位

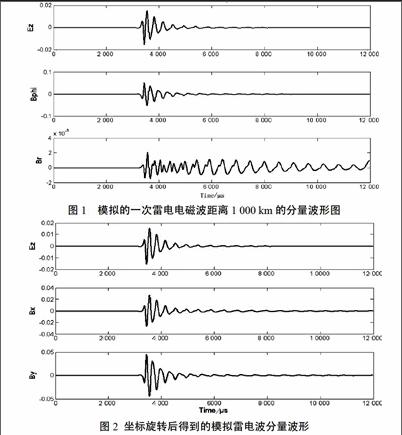
本文利用的是雷电电磁波在地球-电离层波导腔中传播的FDTD计算模型模拟得到雷电波信号的电磁分量，如图1所示。在模拟过程中，电离层的高度选定为典型的夜间高度情况下的86 km，模拟出来的雷电波信号的时间间隔为2 μs，持续时间为12 ms。

下面基于模拟的雷电波信号的3个电磁分量，应用Kharkov方法进行雷电源的定向和定距。通过坡印廷矢量定向的方法（TPDF技术）得到雷电源的方向θ，即完成定向；将笛卡尔坐标系旋转成柱坐标系，将之前的Hx和Hy分解合成为Hφ和Hr，再通过傅里叶变换获得Hr的一阶相位谱，根据选定的频段，将其与波导模型计算得到的相位谱，进行最小二乘法匹配，从而获得雷电源的距离r，完成定距。

2.1 定向

由于雷电电磁波在地球-电离层波导腔中传播的FDTD计算模型只能模拟2 000 km内的雷电，而Kharkov方法能够较为准确地定位距离测站1 000 km以外的雷电。基于这两点，本文选取了距离分别为1 000 km和1 500 km的两次模拟过程进行Kharkov方法的应用。图1是距离为1 000 km时模拟得到的雷电电磁波垂直电场Ez、横向磁场Bφ、径向磁场Br的波形图。

观察波形发现，3个场分量都呈现出多次反射的脉冲状形态，且以一固定频率重复。这个频率接近地球-电离层波导的一阶截止频率f1.

在开始定向前，需要先假定一个方位，将雷电电磁波的横向磁场Bφ和径向磁场Br通过坐标系的旋转，转变为水平磁场Bx和By. 图2为模拟的雷电源在测站的北偏东60°（以正北方向作为0°，顺时针旋转，以下的方位角也是这样定义的）方位上测站获得的3个电磁场分量波形图。

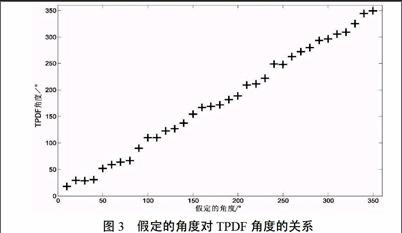
当模拟的雷电源距离测站1 000 km时，利用坡印廷矢量定向获得的方位角为61.518 3°，与之前假定的60°相比，相差约1.5°；当距离选择1 500 km时，计算得到的角度为60.269 2°。为了得到坡印廷矢量定向法的精度和误差分布，本文假定的角度从10°递增到350°，结果如图3所示。

从图3能明显看出，假定的角度与用坡印廷矢量定向法计算得到的角度存在很强的线性关系，两者的相关系数为0.98，角度差的平均值为2.4°，标准差为3.1°。坡印廷矢量在定向的应用中，能较为准确地给出雷电源的方位角，且不存在磁定向法的180°模糊，即能给出雷电源的唯一方向。

2.2 定距

将模拟雷电波径向分量Br的相位与波导模型计算得到的相位进行最小二乘法匹配，从而获得雷电源的距离r，即完成定距，具体如图4所示。

为了直观地显示匹配效果，绘制了模拟雷电波Br的相位图和r=917 km处的依据波导模型计算得到的相位图，如图5所示。从图5可以看出，两者之间的相关性较好，总体变化趋势一致。由此可见，单站定位系统用Br的一阶相位谱定距时的误差较小，可以很好地在闪电发生计算距离。

3 结论

本文应用Kharkov方法对模拟的雷电源进行了定位，主要对雷电发生的位置与测站之间的方位、距离进行了计算，得出了以下结论：①通过假定的雷电源方位与由坡印廷矢量计算得到的方位进行比较，两者之间的差异较小，平均值为2.4°，即用坡印廷矢量进行定向的方法是可行；②通过Br一阶相位谱与在最小二乘法匹配得到的距离处用波导模型计算得到的相位谱进行比较，误差较小，可以很好地对雷电发生时的距离进行计算。

参考文献

[1]李贤.雷电定位系统的优化设计与实现[D].北京：北京邮电大学，2010.

[2]A FEW. Lightning channel reconstruction from thunder measurements.Journal of Geophysical Research，1970，75（36）.

[3]都百万，王保强.雷电监测方法的研究[J].成都信息工程学院学报，2007，22（02）.

[4]Burke C P，Jones D L.An experimental investigation of ELF attenuation rates in the Earth-ionosphere duct. Journal of Atmospheric & Terrestrial Physics，1992，54（04）.

[5]李蕾.新一代閃电定位设备的研制[D].西安：西北工业大学，2001.

[6]陈亚洲，乔治军，刘尚合，等.雷电电磁脉冲对电火工品的发火危险性研究[J].兵工学报，2001，22（03）.

[7]Rafalsky V A， Nickolaenko A P， Shvets A V， et al. Location of lightning discharges from a single station. Journal of Geophysical Research Atmospheres，1995，100（D10）.

〔编辑：张思楠〕