乘幂拟合法在确定洛特卡分布和定律参数中的应用*

张海燕

乘幂拟合法在确定洛特卡分布和定律参数中的应用*

张海燕

乘幂拟合是曲线拟合的一种类型。洛特卡定律的数学表达式yx=C/xn本身就是乘幂的形式，根据曲线拟合后所对应的乘幂方程，可以直接得出n值和C值，非常简便准确。

乘幂拟合 洛特卡定律 分布 参数 K-S检验

1 洛特卡定律的基础性研究现状

目前业界对洛特卡定律的基础性研究薄弱、墨守陈规。在洛特卡定律的基础性研究中，继20世纪90年代张贤澳[1-3]后鲜有人问津，严重制约了文献计量学的发展和应用。计算机技术的发展和各种便捷高效的统计软件出现为改善文献计量学的基础研究方法提供了可能。文献计量学归根到底是应用学科，只有不断引入先进的分析工具才能推动其发展。

1.1 n值及C值的一般求法繁琐

在洛特卡定律的数据统计和分析过程中，现在普遍采用的是1986年由美国学者米兰德·李·鲍(Miranda Lee Pao)提出的以普赖斯和扬布兰斯基准则为依据的删除离差大的高产著者的数据，逐一拟合比较，从中选出最优的回归直线的方法，即以回归分析为基础的拟合方法[4]。但是n值及C值的一般求法非常繁琐(详见下面公式)，很容易在计算过程中出现错误。

1.2 高产作者的确定方法模糊

在实际应用过程中，洛特卡定律只适用于作者群体中占绝对数量优势的低产作者，而高产作者作为特殊群体，不适用于洛特卡定律，所以要将高产作者的数据删除。而为了方便起见，高产作者往往按照作者总数的1%或者是按普莱斯定律就是科学家总人数开平方所得到的人数来确定。之所以这样处理，原因并不明确，因此高产作者的数据都是估算的，缺乏严谨的解释说明。

2 乘幂拟合法在确定洛特卡分布和定律参数中的应用

现在其实完全可以通过利用常用的统计软件如Excel来解决这一类过去难以突破的问题。在Excel的图表向导中，通过添加趋势线的方法来选择最合适的分析类型对数据进行拟合是可行的解决方案。在运用洛特卡定律时，可以通过以下步骤来实施：

2.1 选择合适数据

对论文数和作者数各取对数后，在Excel的图表向导中选择线性关系对这两组数据进行拟合，在全部数据中选取连续多组数据逐一进行线性拟合比较，参考相关系数并从中选出最合适的拟合直线。而不在线性范围内的那一部分高产作家数据就是要被删除的数据，所以要去掉的高产作家不一定刚好是总人数的1%，也不一定是总人数开平方所得到的人数，而是不在线性范围内的那一部分。这和米兰德·李·鲍的删除离差大的高产著者的数据是一致的。

2.2 求n值和C值即洛特卡分布参数

对选择好的数据进行下一步分析。算出各个作者数在总作者数中(已经删除高产作者)的百分比，然后对论文数和作者百分比这两组数据在Excel的图表向导中选择乘幂关系进行拟合。笔者发现，选择乘幂的分析类型是最直接和准确的。洛特卡定律的数学表达式yx=C/xn本身就是乘幂的形式，根据曲线拟合后所对应的乘幂方程，可以直接得出n值和C值，非常简便和准确。

2.3 K-S检验

在乘幂拟合或线性拟合的图形中，通过观察第一组数据理论值与实际值的吻合度，可以初步判断该组数据能否通过检验，计算出第一组数据的差值D1和D临界，如果D1＞D临界，就可以判断该组数据不能通过K-S检验，也不用再进行其它数据的计算，从而简化K-S检验过程。

综合运用线性拟合和曲线拟合两种方法，先通过线性拟合选择合适的研究数据，再对其进行乘幂拟合从而直接得出洛特卡分布函数表达式的方法直观、简便，值得推广。

3 例证

本文以3例文献数据来解释乘幂拟合法在确定洛特卡分布和定律参数中的应用。

例1采用邱均平等发表在《图书情报研究》2009年第2期论文中的表7[5]的数据，制成表1。

表1 1978-1982年情报学作者分布表

因原表取前6组数据计算，故亦取同样数据绘制图1。

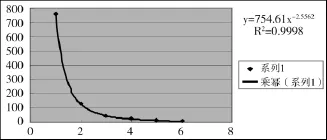
图1 作者原始数据的乘幂拟合图(对应于表1)

可见，论文数x与作者数y相关良好，且最高点基本为曲线起点，即x=1时的y值的理论值和实际值吻合度高。故初步推断该组数据符合洛特卡分布。

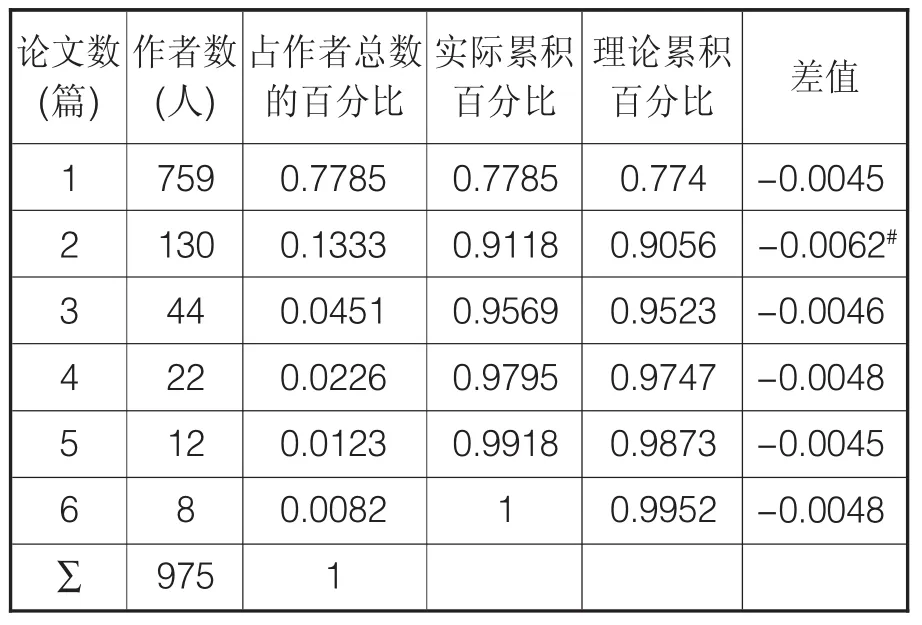
表2 1978-1982年情报学作者分布的K-S检验表

取显著性水平α=0.01时，D临界=1.63/√975=0.0522，Dmax=0.0062，故Dmax＜D临界，该组数据可以通过K-S检验。与原文结果一致。

图2中乘幂方程式y=0.774x-2.5563(x=1，2，……)即洛特卡分布函数表达式，与原文结果F (x)=0.76407x-2.57348基本相符，细微差别是由于在计算过程中有效数字的处理略有差异造成的。

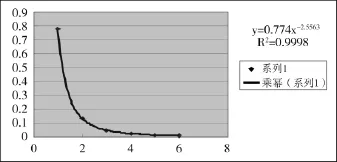
图2 作者百分比的乘幂拟合图(对应于表2)

例2采用李丽娜发表在《情报杂志》2009年第5期论文中的表2[6]的数据，制成表3。

表3 十年间我国图书情报领域论文文献的作者分布

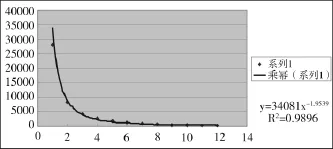
图3 作者原始数据乘幂拟合图(对应于表3)

原文取表中12组数据研究，本文亦然。可见，论文数x与作者数y相关尚好，但拟合曲线的起点即理论最高点比实际最高点高出很多，即x=1时的y值的理论值和实际值相差甚远，故初步推断该组数据不能通过K-S检验。

取显著性水平α=0.01时，D临界=1.63/√49084=0.0073；x=1时的y值的理论百分比与实际百分比的差值D1=(34081-28214)/49084 =0.1195，故D1＞D临界，其它累积差值可以不计算了，该组数据不能通过K-S检验。这与原文的检验结果一致；n=1.9539也与原文结果n=1.954相符。

例3 采用邱均平等发表在《图书情报工作》2011年第10期论文中的表4[7]的数据，制成表4。

表4 2007-2010年科学网信息科学学科博文博主分布情况

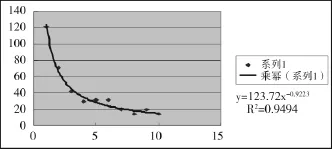
图4 博文与博主原始数据乘幂拟合图(对应于表4)

原文取全部10组数据研究，本文亦然。可见，博文数x与博主数y相关尚好，但可以看出最高点与理论值有偏差，故先取x=1时的差值D1进行比较。

取显著性水平α=0.01时，D临界=1.63/√392=0.0823；x=1时的差值 D1=(123.72-121)/392=0.1195，故D1＞D临界，其它累积差值则不必计算了，该组数据不能通过K-S检验。这与原文结果一致；n=0.9223与原文结果n=0.92228相符。

通过以上3个例子可以看出，在确定洛特卡分布和定律参数的过程中，乘幂拟合作图法与常规使用的公式法的结果完全一致，证明这种方法可行；而且采用这种方法可以大大减少易于出错的繁琐的计算过程，同时对洛特卡定律的理解和把握更直观且准确。

4 结语

在文献计量学发展的各个不同阶段，洛特卡定律表现出强大的生命力，其持续发展而成为科学研究不可或缺的重要量化工具。国内外图书情报学者对它的完善和发展进行了积极探索，且成果丰硕。很多科研团队都会在自己的研究领域中通过运用洛特卡定律来寻找该领域的核心作者等重要信息，加深对研究主题的认识，并进一步找到研究方向。

可是洛特卡定律是几十年前产生的经验定律，当时研究者只能借助手工统计和计算，过程非常繁琐且易于出错。现在可以用更为先进有效的统计手段来化繁为简。本文通过借助于数据统计软件Excel，没有采用线性拟合的常规方法，而是改为直接使用曲线拟合的方法，通过对论文数及相应作者原始数据或百分比数据进行乘幂拟合，试图在方法学上对洛特卡定律有所改进。本文选取3个例证来解释乘幂拟合如何在确定洛特卡分布和定律参数中发挥作用，与常规方法相比，因为线性拟合需要将论文数和作者数都转化为对数后再进行处理而使过程略显麻烦，此时乘幂拟合直接简便的优势非常突出，当然这是建立在Excel强大的统计功能基础上的。但是乘幂拟合的数据效果特别是对高产作者的剔除不如线性拟合更直观明显。所以对于洛特卡定律，综合运用线性和乘幂的分析方法较为合适，即先通过线性拟合选择合适的研究数据、删掉不合适的高产作者数据，再对选择后的数据进行乘幂拟合从而直接得出洛特卡分布的函数表达式。同时注意观察图像中的高点位置，据此来初步判断研究数据能否通过K-S检验，从而简化K-S检验过程。本文采用的作图法较之常规使用的公式法更为直观简便，类似这种方法学上的改进，还可以应用在其它文献计量学定律如布拉德福定律等的研究上，值得在各学科和各领域文献的计量学研究方面推广。

[1]张贤澳.非回归分析的洛特卡定律参数n、c的直接估算[J].图书情报工作，1991（12）：27-35.

[2]张贤澳.洛特卡定律研究的方法探讨[J].图书情报工作，1995（3）：11-18.

[3]张贤澳，李美文.广义洛特卡定律参数特征的研究[J].情报探索，1996（6）：10-15.

[4]M.L.Pao.An Empirical Examination of Lotka's law[J]. Journal of American Society for Information Science，1986（1）：29-31.

[5]邱均平，杨思洛，王明芝.改革开放30年来我国情报学研究的回顾与展望（二）—情报学研究论文的作者分析[J].图书情报研究，2009（2）：8-13.

[6]李丽娜.多角度对图书情报领域洛特卡分布的验证[J].情报杂志，2009（5）：5-7.

[7]邱均平，余凡.网络学术信息作者分布规律研究——以科学网博客为例[J].图书情报工作，2011（10）：15-18.

Applying Exponentiation Fitting to Determine Lotka's Distribution and the Parameters of Lotka's Law

ZHANG Hai-yan

Fitting Exponentiation is a type of curve fitting and the mathematical expression of Lotka's law yx=C/xnis a form of exponentiation.According to the exponentiation equation，N and C values can be obtained directly and simply.

exponentiation fitting；Lotka's law；distribution；parameters；K-S test

格式 张海燕.乘幂拟合法在确定洛特卡分布和定律参数中的应用[J].图书馆论坛，2014（1）：18-21.

张海燕（1978-）女，硕士，广东药学院图书馆馆员。

2013-03-29

*本文系广东药学院人文思政研究专项课题“医学领域论文的计量规律研究”（课题编号：RWSZ201123）研究成果之一