《信息论与编码技术》课程中平均互信息的教学探讨

陈燕燕

（华侨大学 厦门工学院，福建 厦门 361021）

《信息论与编码技术》课程中平均互信息的教学探讨

陈燕燕

（华侨大学 厦门工学院，福建 厦门 361021）

平均互信息是信息论与编码技术中用来计算信道容量、信息率失真函数和信道剩余度的重要物理量。通过一道典型例题来讲解求平均互信息的不同方法：根据平均互信息的定义求、根据损失熵求、根据噪声熵求、根据信息熵的强可加性求，最后用MATLAB语言进行编程验证，实验表明四种方法求出的结果是一致的。在课堂教学时，教师应鼓励学生灵活运用各种方法，做到举一反三。

平均互信息；定义法；损失熵法；噪声熵法；强可加性法

《信息论与编码技术》是电子类相关专业的一门重要的专业必修课，其中自信息量、信息熵、互信息都是为学习平均互信息做铺垫的，而平均互信息又是求解信道容量、信道剩余度和信息率失真函数的重要工具。在教学过程中，学生反映平均互信息概念抽象，计算复杂，公式颇多，难以区分。由于学生的基础相对薄弱，不能灵活运用公式推导和基本性质相结合进行求解。因此，在课堂教学中，采取淡化数学推导，重点讲清平均互信息的实际意义、作用等，关键是如何应用平均互信息的定义、信息熵的性质等计算出平均互信息。平均互信息的计算方法有多种，如根据平均互信息的定义求、根据损失熵求、根据噪声熵求、根据信息熵的强可加性求等。

下面通过教材[1]一个典型例题来探讨平均互信息的四种求解方法，并通过MATLAB编程来验证结果的正确性。

一、例题讲解

题目：已知信源X的概率p（x）和信道传递概率p（y|x）分别如下所示：

求平均互信息I（X；Y），并用MATLAB验证结果。

首先分析题目：题目中只给出了两种概率分布，而对于输出符号Y的概率P（y）、联合概率P（xy）和条件概率P（x|y）均未给出，因此，必须先求出它们，以方便下面进行求解。

求解方法：为了简单直观，这里教学生采用矩阵的方法来求解。

注意：这里跟实际矩阵的求法又有区别，这里在上课时要重点强调。

注意：这里也要注意求条件概率P（x|y）时，尤其要弄清楚对应关系。

下面逐一介绍求平均互信息的各种方法，以及每种方法的重点、难点和注意事项。

1.根据平均互信息的定义求。平均互信息的定义[2]为：互信息I（x，y）在两个概率空间X和Y中的统计平均值称为平均互信息，代表接收到输出符号Y后平均每个符号所获得的关于输入X的信息量。

分析求解：平均互信息既然是互信息的平均值，那就利用概率论与统计课程中学到的求平均值的方法来求解。即：

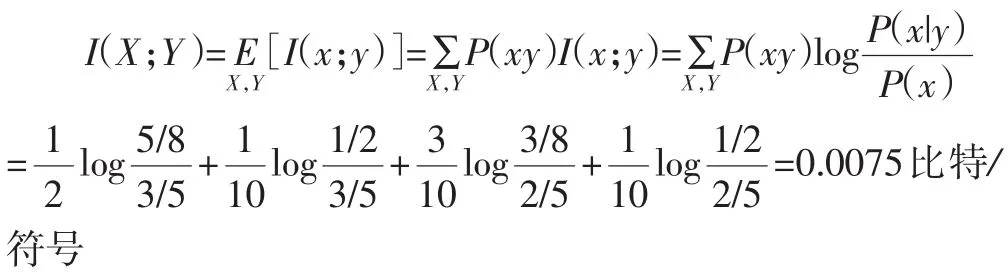
注意：在此种方法中，学生对于求统计平均已经忘记了，所以容易将P（xy）写成P（x），导致错误的结果。

2.根据损失熵求。损失熵的定义为：H（X|Y）称为损失熵，表示在接收端收到输出变量Y的符号后，对于输入端的变量X尚存在的平均不确定性。

分析求解：由于H（X）是在接收到输出Y以前，关于输入变量X的先验不确定性的度量。可见，通过信道传输后排除了一些不肯定度，从而获得了部分信息，就是平均互信息。故I（X；Y）=H（X）－H（X|Y）

注意：在此种方法中，学生容易把H（X|Y）写成H（Y|X），导致错误的结果。

3.根据噪声熵求。噪声熵的定义为：H（Y|X）表示在输入已知的前提下，对输出变量存在的不肯定度。接收端收到的关于输入X的平均信息量I（X；Y）加上H（Y|X）等于信源Y的熵H（Y）。H（Y|X）反映了信道中噪声源的不确定性，故叫噪声熵。

分析求解：既然H（Y）=I（X；Y）+H（Y|X），则I（X；Y）= H（Y）－H（Y|X）。

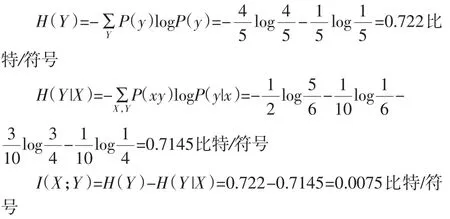
注意：在此方法中，学生容易把H（Y|X）写成H（X|Y），导致错误的结果。

4.根据信息熵的强可加性求。信息熵的强可加性[3]：

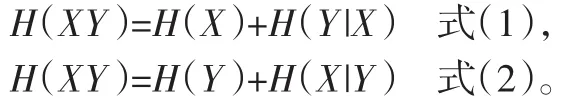
分析求解：由于熵的强可加性有两个公式，所以这里又有两种方法来求解。

方法一：利用公式（1）求解；

因为I（X；Y）=H（Y）－H（Y|X），将公式（1）带入可得，

方法二：利用公式（2）求解；

因为I（X；Y）=H（X）－H（X|Y），将公式（2）带入可得，

可以看出，公式（3）和公式（4）是一样的，因此，不管用哪个强可加性公式，最后的结果都是一样的。所以接下来利用I（X；Y）=H（Y）+H（X）－H（XY）来求平均互信息。

H（X）和H（Y）在上面已求出，所以这里只需求联合熵H（XY）即可。

故I（X；Y）=H（Y）+H（X）-H（XY）=0.722+0.971－1.6855= 0.0075比特/符号

注意：学生在记H（XY）=H（X）+H（Y|X）这个强可加性公式时，总是误把H（Y|X）记成H（X|Y），这里教学生一个记忆的方法，就是看前面的被加数是什么，如果前面的被加数是H（X），那么后面的加数就是条件为X的噪声熵H（Y|X）；相反，如果前面的被加数是H（Y），那么后面的加数就是条件为Y的损失熵H（X|Y）。但是在求平均互信息时，不管用哪个强可加性公式，最后都是用联合熵H（XY）来求平均互信息。

二、MATLAB编程及实验结果分析

利用MATLAB编程实现上述四种求平均互信息的方法，程序在此不一一列出，但程序运行结果显示都为0.0075，与上述四种计算方法计算出来的结果是一致的。

三、结论

通过一道求解平均互信息的例题，使用四种方法：根据平均互信息的定义求、根据损失熵求、根据噪声熵求、根据信息熵的强可加性求，并利用MATLAB语言编程验证结果是正确的。表明：定义求解需要注意是利用互信息乘以联合概率；根据损失熵求解需要知道损失熵是H（X|Y）；根据噪声熵求解需要知道噪声熵是H（Y|X）；根据信息熵的强可加性求解，需要区分强可加性公式中到底用的是H（X|Y）来转化还是利用H（Y|X）来转化，但是不管用哪个，最后都是用联合熵H（XY）来求解。在教学中尽力开拓学生的思维，让其注意每种方法的区别和联系，并选择自己擅长的方法来求解，达到能够举一反三的目的。

[1]傅祖芸.信息论—基础理论与应用[M].北京：电子工业出版社，2011.

[2]曹雪虹.信息论与编码[M].北京：清华大学出版社，2004.

[3]李亦农.信息论基础教程[M].北京邮电大学出版社，2005.

G642.41

A

1674-9324（2014）28-0091-03

陈燕燕（1986-），女，江西赣州人，华侨大学厦门工学院电子信息工程系助教，硕士研究生，研究方向：网络，编码。