工业机器人轨迹衔接方法研究
2014-03-09郭霞刘鹏飞段晓妮
郭霞,刘鹏飞,段晓妮
(1.西安交通大学城市学院电器与信息工程系,陕西西安 710018; 2.航天科技集团第16研究所,陕西西安 710100)
工业机器人轨迹衔接方法研究
郭霞1,刘鹏飞2,段晓妮2
(1.西安交通大学城市学院电器与信息工程系,陕西西安 710018; 2.航天科技集团第16研究所,陕西西安 710100)
在笛卡尔空间下的机器人轨迹规划中,常用一段“小圆弧轨迹”衔接运动过程中的前后两条轨迹,以达到不用把速度降到0就能平稳拐弯的目的。对高速高精度机器人而言,平稳拐弯要求轨迹足够平滑,而小圆弧过渡方法会使关节的加速度轨迹发生跳变而影响轨迹的平滑性。针对这一不足,提出用五次多项式插值的方法平稳衔接两条轨迹,推导了该五次多项式系数矩阵的求解方法。通过仿真验证表明,新方法能使轨迹更加平滑。
工业机器人;笛卡尔空间;轨迹衔接;多项式插值
工业机器人在笛卡尔空间的运动轨迹通常有直线(MOVL)、圆弧(MOVC)和样条曲线(MOVS)。单条轨迹是难以完成任务的,一项加工作业往往由多条轨迹顺序衔接完成。然而,两条轨迹在衔接处存在一个尖角,在机器人连续运动的情况下,这个尖角易使机器人产生振动。针对这一问题很多学者提出了改进措施。例如,用小圆弧取代这个尖角[1],用已知的误差界限求解出第一条直线尾端的拐弯点和第二条直线始端的拐弯点,两拐弯点间用圆弧匀速衔接。文献[2]用了相似方法并做了改进,给衔接的圆弧轨迹做了加减速的处理,使运动轨迹其沿着圆弧切线方向的速度连续变化。
在高速高精度工况下,不但要求机器人关节的转角和速度连续,为了平稳,要求关节的加速度也是连续的。但是,圆弧过渡的方法不能使加速度也保持连续,下面进行分析。
1 加速度轨迹突变的问题
如图1所示,圆弧过渡方法以两条轨迹在拐弯点(图1中的圆圈)的位置坐标和速度矢量为已知条件,用一段圆弧连接两条轨迹。该方法可以保证机器人末端轨迹的连续和速度轨迹的连续。但是,圆弧运动需要有向心加速度实时地改变其运动方向,只要在拐弯点处的速度不为零,向心加速度就必须突然存在。也就是说,在由直线末端切入到圆弧时,在切点处必须提供这一向心力,这是突变过程。只有圆弧切向速度为零才可避免向心加速度突变,而用圆弧过渡取代尖角就是为了避免速度降为零,显然这是矛盾的。
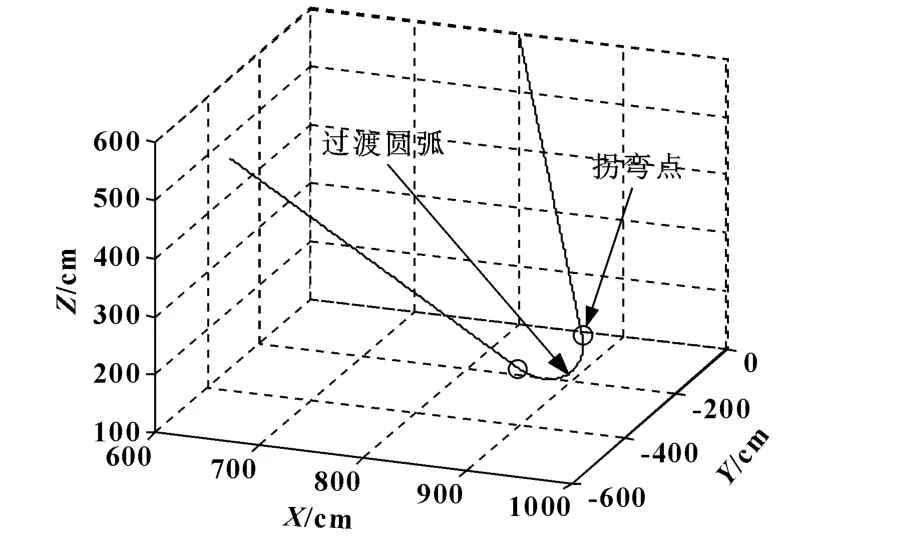
图1 圆弧过渡轨迹仿真图
图2是用圆弧过渡方法衔接两条直线轨迹时加速度模值轨迹的变化过程,可以看出加速度在拐弯点产生了突变,这是突然产生的向心加速度。

图2 圆弧过渡过程加速度的变化轨迹
向心加速度的突然出现会对关节空间的轨迹产生怎样的影响?由于关节机器人正反解的复杂性,不容易做出定量的分析。但可以确定的是:笛卡尔空间和关节空间的映射关系是连续的,在笛卡尔空间的加速度突变会导致关节空间加速度的突变。这种突变可能导致两种结果,一是关节电机电流过载,二是电机电流受到上限的限制导致轨迹跟踪的误差或振动。
2 基于五次多项式插值的轨迹衔接方法
针对加速度轨迹突变的问题,使用基于五次多项式插值的方法来衔接两条轨迹。下面以“直线-直线”轨迹衔接为例进行论述。
如图3所示,Pe1是第一段直线的拐弯点,Pe2的第二段直线的拐弯点。根据轨迹规划算法[3-4]和给出的误差界限re1=|Pe1-P2|和re2=|Pe2-P2|可以反算出拐弯点Pe1和Pe2的位置、速度和加速度坐标,它们表示符号分别为Pe1、Pe2、Ve1、Ve2、ae1、ae2,其中Pe1=[xe1ye1ze1]T,其余各量也都为向量表达式。

图3 “直线-直线”衔接示意图
过渡曲线为五次多项式,表达式表述如下:

为求式中的6个系数矩阵A~F,有边界条件如下:
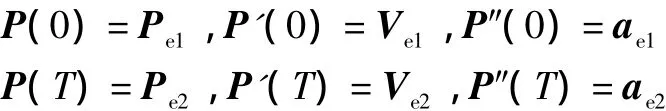
其中T是过渡轨迹的运动时间,可由公式求取:

其中k∈[1.5,3],该参数可对过渡时间做微调。
于是,可以解得各参数矩阵如下:

假设机器人姿态保持不变,姿态旋转矩阵为R,基于五次多项式插值的轨迹衔接方法表述如下:
(1)根据误差界限re1和re2计算前后两段被衔接轨迹的拐弯点的信息Pe1、Pe2、Ve1、Ve2、ae1、ae2;
(2)将拐弯点的信息作为边界条件求解五次多项式表达式P(t);

(4)将齐次变换矩阵F(t)反解到获得关节轨迹q(t)。
3 仿真结果与分析
下面用基于五次多项式插值轨迹衔接的方法对一段“直线-直线”衔接过程进行仿真。直线用‘S’型加减速策略[3]。机器人本体模型选用中国航天科技集团第十六研究所的SC-8A型6R垂直关节机器人,该型机器人的D-H参数如表1所示,依据该参数可以推导出机器人的正解和逆解,在此不做论述。

表1 SC-8A垂直关节机器人D-H参数
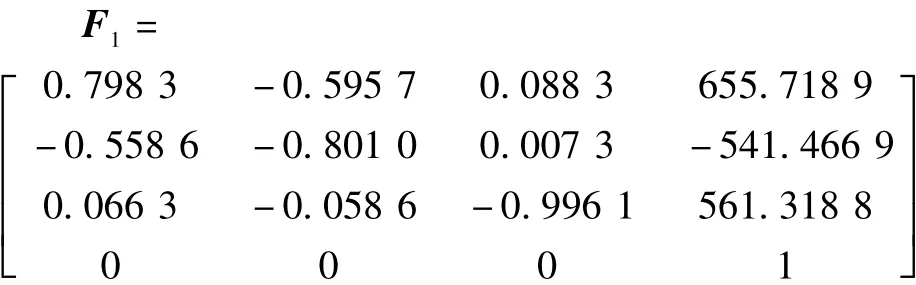
两段被衔接的直线轨迹初始信息如下:
第一段直线轨迹的起始位姿为:

第二段直线轨迹的起始位姿和第一段轨迹的终点位姿F2重合,终点位姿为:

在笛卡尔空间的仿真轨迹如图3所示。机器人的姿态保持不变,运用逆解公式将笛卡尔空间下的轨迹变换到关节空间下得到6个关节的变化轨迹如图4(a)所示。
上述的两条直线轨迹分别用基于五次多项式插值的过渡方法和小圆弧过渡的方法做衔接比较,仿真结果如图4—6所示。其中,图4为机器人6个关节转角轨迹的对比,图5为机器人6个关节速度轨迹的对比,图6为机器人6个关节加速度轨迹的对比。从图4和图5中可以看出,两种方法下的关节转角轨迹和关节速度轨迹都满足连续性要求;在图6中,用小圆弧过渡方法的关节加速度轨迹在衔接阶段出现了明显突变,而用基于五次多项式插值的过渡方法的关节加速度轨迹连续性很好。
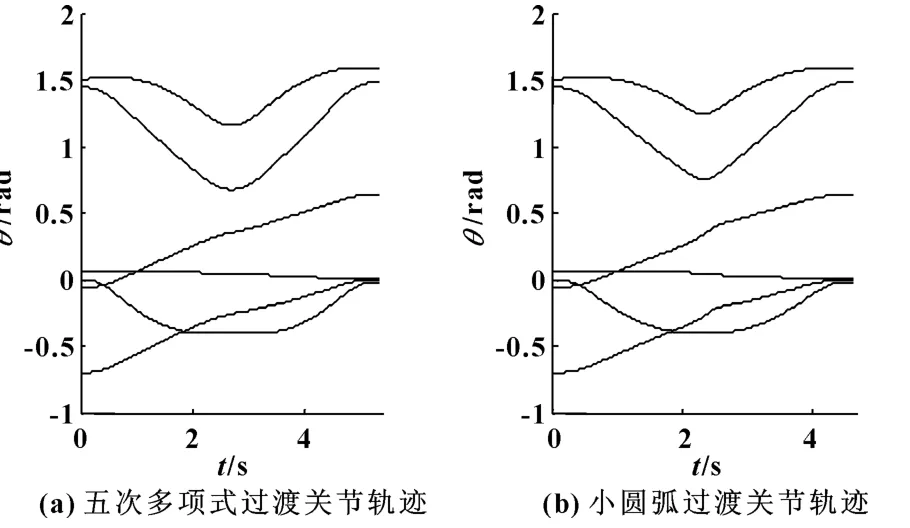
图4 两种过渡方法关节轨迹对比
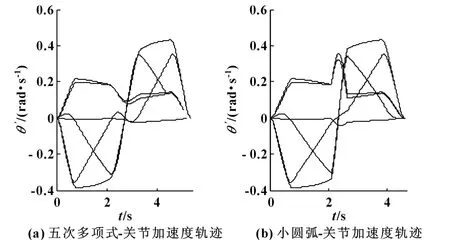
图5 两种过渡方法关节速度对比
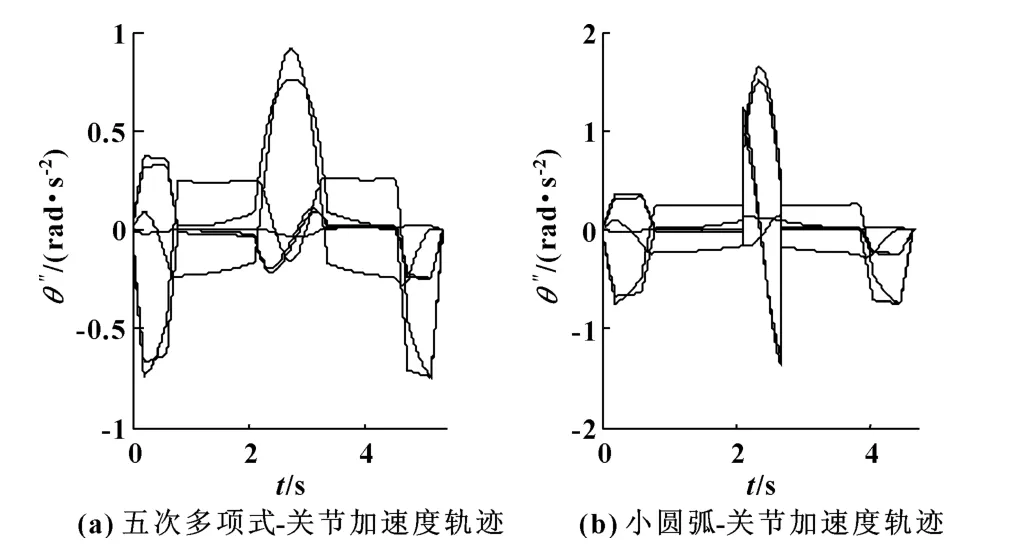
图6 两种过渡方法关节加速度对比
4 结论
用五次多项式插值的方法可以平稳衔接两段笛卡尔轨迹,衔接过程关节的角度、角速度、角加速度均保持平滑。关节角加速度与关节电机的电流呈正比关系,平滑的角加速度可使关节电机工作在更加柔和的运动控制指令下。在轨迹平滑性要求较高的应用场合,如高速、高精度机器人,具有很好的实用性。
[1]陈伟华.工业机器人笛卡尔空间轨迹规划研究[D].广州:华南理工大学,2010:37-41.
[2]蓝培钦.码垛机器人控制系统软件的设计和研究[D].上海交通大学硕士学位论文.2010.2:45-48.
[3]TAYLOR R.Planning and Execution of Straight Line Manipulator Trajectories[M].Robot Motion,Brady et al.Editors,MIT Press,Cambridge,MA,1983:424-436.
[4]PAUL R.Manipulator Cartesian Path Control[J].IEEE Transactions on Systems,Man,and Cybernetics,1979,9 (11):703-711.
[5]刘鹏飞,杨孟兴,宋科,等.‘S’型加减速曲线在机器人轨迹插补算法中的应用研究[J].制造业自动化,2012,34(10):4-8.
Study about Trajectories Connecting Method of Industry Robot
GUO Xia1,LIU Pengfei2,DUAN Xiaoni2
(1.Xi'an Jiaotong University City College,Xi'an Shaanxi 710018,China; 2.The 16thInstitute,China Aerospace Science and Technology Corporation,Xi'an Shaanxi 710100,China)
In the trajectory planning of industry robot in Cartesian space,a small“arc-curve”is always used to connect two trajectories in order to change the moving direction smoothly without decreasing velocity down to zero.It requires trajectory smooth enough to turn the direction during a high-speed and high-precision operation of industry robot.However,the small“arc-curve”would bring mutations to the trajectory of acceleration.To avoid such disadvantage,a new connection method based on 5th-order polynomial interpolation was proposed,and some derivations which showed how to compute the coefficient matrix of the polynomial were listed.The simulation attests that the new method connects two trajectories more smoothly.
Industry robot;Cartesian space;Trajectory connection;Polynomial interpolation
TP242
A
1001-3881(2014)9-010-3
10.3969/j.issn.1001-3881.2014.09.003
2013-05-07
国家战略性新兴产业高端装备专项([2012]432号)
郭霞 (1980—),女,硕士,研究方向为智能控制。通信作者:刘鹏飞,E-mail:lpf_8748@yahoo.com.cn。
