不同固结系数计算方法之间的比较
2014-03-07骆凉平丁建文
骆凉平 丁建文
(1.河海大学岩土力学与堤坝工程教育部重点实验室,南京 210098;2.河海大学岩土工程研究所,南京210098;3.东南大学交通学院岩土工程研究所,南京 210096)
固结系数是反映土体固结快慢的重要指标,为了计算固结度的变化或是超静孔压消散过程,都需要给出固结系数.传统的计算固结系数的方法是通过对太沙基一维固结理论的固结度计算公式进行简化,根据一维固结压缩试验所确定的时间-变形关系曲线,推导出固结系数的近似计算公式,从而获得土体固结系数,例如时间对数法、平方根法等.这些方法都是图解法和经验配合法,根据压缩曲线判断主固结起始点d0及固结点d90、d100,在绘图过程中易受人为因素干扰,因此具有一定的误差.
除了依据时间-变形关系曲线计算固结系数,也有一些学者应用孔压测量装置对土体固结过程进行分析.孔压法的优势在于可最直接地判断主固结的结束,与其他间接判断方法相比更具可靠性.Taylor[1]很早就对固结过程中的孔压消散情况进行研究,Olson[2]研究发现,仅仅依据孔压消散数据而不考虑变形曲线计算得出的固结系数与基于时间-变形曲线计算所得的固结系数在某些情况下会出现较大偏差.
此外,尽管孔压法在判断主固结沉降时具有直接、准确的优点,但在实际试验过程中,孔压装置所测的底部孔压数据与太沙基一维固结理论并不吻合,不能直接应用于计算固结系数.首先,试验中测得的最大孔压数值小于所施加的竖向有效荷载;其次,施加竖向荷载后,底部孔隙水压力不会立即上升至最大值,而是具有一个滞后过程.Gibson[3]、Whitman[4]等很多学者都曾在试验中发现这一现象并对此进行研究,认为造成这一现象的原因主要是由于孔压计的测压机理和土颗粒的压缩变形.Perlof[5]研究认为这一现象只在固结初期对孔压数据产生影响,当试样达到一定固结度之后,对于孔压数据的影响则可以忽略不计,所测孔压仍可应用于固结过程分析中,随后,Robinson[6]也通过试验验证了这一观点.据此,本文以连云港粘性土作为研究对象进行一维固结压缩试验,在固结过程中随时测量其超静孔隙水压力,针对孔压消散阶段的数据进行分析,并结合孔压数据和时间-变形关系曲线计算各级荷载下的固结系数,并与时间对数法和时间平方根法的计算结果进行对比.
1 理论依据
土体压缩通常分为3个阶段:瞬时沉降、主固结沉降和次固结沉降.太沙基一维固结理论就是描述土体主固结阶段的压缩特性,本文假设在主固结阶段,土体变形仅仅是由于土中孔隙水被排出,超静孔压消散而引起的,并不发生次固结变形.基于这个假设,则在室内一维固结试验中,试样底部超静孔隙水压力与压缩变形呈线性关系(Robinson[6-7]).Crawford[8]针对渥太华海相沉积粘性土进行研究时也发现了超静孔压与沉降的线性关系.
当采用超静孔压进行固结度计算时,其公式为

式中,σ为施加于土样的竖向荷载增量,ub为试样底部孔隙水压力.
由于前述超静孔压与沉降呈线性关系,则根据上式,土样的固结度与沉降也呈线性关系,如图1所示.由图1可见,该直线与纵轴的交点d0、d100分别是固结度等于零和固结度等于100%时的沉降量.
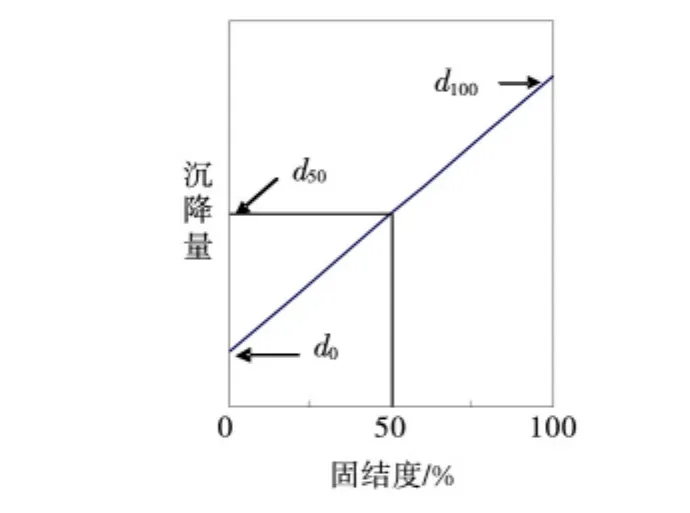
图1 固结度与沉降关系示意图
由此,结合一维固结压缩试验的时间-变形曲线可求得土样在任意固结度下所对应的固结时间,再根据太沙基一维固结理论固结度计算公式:
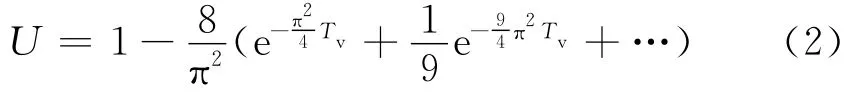
计算该固结度下的时间因素Tv,即可求得试样在某一级荷载下的固结系数.本文将选取固结度为U=50%时所对应的固结时间t50计算固结系数,固结系数计算公式为

式中,H为固结试验中最大排水距离,由于本文试验将在试样底部测量超静孔隙水压力,故仅从试样顶部排水,最大排水距离即为土样厚度;t50为固结度达到50%是所对应的固结时间.
2 试样物理特性及试验仪器
试验用土取自江苏连云港地区,基本物理参数见表1.其中液限采用蝶式液限仪测定,塑限采用搓条法测定,粒径分布采用密度计法测定.该土在塑性图上的位置如图2所示,略微高于A线,属于高液限黏性土.

图2 塑性图

表1 连云港土的的基本物理参数
本文试验采用Zeng等设计改进的能够测量试样 底部孔压的渗透固结容器,如图3所示,代替常规固结容器进行固结压缩试验.孔压测量装置由孔压计和与之相连的数字显示器组成,测量精度为1kPa,在固结过程中可随时显示试样底部孔隙水压力.为保证试样底部透水石和测压管道完全饱和不含气泡,固结容器底部还配备有渗透装置.试验制备土样为完全重塑饱和土,初始含水率为1.6倍液限,试样直径为61.8 mm,高度为40mm.

图3 可进行底部孔压测量的固结容器(Zeng等[9])
3 试验结果与分析
3.1 压缩曲线和孔压变化规律
通过上述底部可测孔压的固结仪进行固结试验,所得的连云港重塑黏土的d-logt压缩曲线如图4所示,加载等级分别为50kPa、100kPa、200kPa、400 kPa、800kPa和1600kPa,压缩曲线呈倒S形,具有两个反弯点.运用孔压法计算固结系数时需根据压缩曲线确定d50时对应的固结时间t50,进而根据公式(3)计算固结系数.

图4 连云港重塑黏土时间-变形压缩曲线
图5是与各级荷载下压缩曲线相对应的试样底部超静孔隙水压力随时间的变化曲线.由图5可知,孔压随时间变化呈现先增大后减小的规律,约在30 min达到峰值,并且峰值孔压低于竖向荷载增量,约等于荷载增量的50%.这一试验结果与Whitman[4]、Robinson[6]等人的试验研究是一致的.造成这一现象的原因是试样底部超静孔隙水压力的产生需要一定的时间,在这一过程中试样顶部同时在排水,所以导致了峰值孔压的延迟并使其小于竖向荷载增量.

图5 连云港重塑黏土底部孔压与固结时间关系曲线
根据所测试样底部超静孔压以及固结度计算公式(1)可计算试样固结度,据此,在固结过程中,根据孔压消散情况计算所得固结度与试样变形的关系如图6所示.

图6 连云港重塑黏土固结度与沉降量关系曲线
由图6可知,由于试样底部超静孔隙水压力的延迟作用,连云港重塑黏土在50~100kPa、100~200 kPa、200~400kPa、400~800kPa、800~1600kPa 5个荷载增量下,固结度均随着沉降量的增加先减小后增大,当固结度大于一定程度时,固结度随沉降量的增加线性增大.在上述5个荷载增量下,固结度分别超过46%、35%、47%、51%、58%后,固结度与沉降量呈线性变化规律,通过拟合方法可获得这些直线的方程,其与纵轴的交点就对应于固结度为0和固结度为100%时的沉降量d0、d100,进而可计算出t50和Cv.
3.2 与时间对数法、时间平方根法的比较
运用时间对数法和时间平方根法计算连云港重塑黏土在不同竖向荷载下的固结系数,并与前述方法进行对比.其中,根据时间对数法确定的固结度为100%时对应的沉降量d100与基于底部超静孔压所确定的d100对比如图7所示,由图可知,数据点均位于45°线附近,由时间对数法确定的主固结沉降量略低于基于孔压测定的主固结沉降量,但二者差异较小.可见时间对数法确定主固结沉降量具有良好的精度.

图7 孔压法测定d100与时间对数法估测值的比较
将时间平方根法、时间对数法及基于孔压计算的固结系数进行比较,如图8所示,图中空心点位于实心点的上方,并且实心点相对更靠近45°线.可见时间平方根法计算的固结系数Cv大于时间对数法的计算结果,这与很多学者的研究是一致的.而时间对数法确定的固结系数Cv更接近本文采用的孔压法,二者的计算结果非常接近45°线.因此,在缺乏孔压数据的情况下,本文建议使用时间对数法计算固结系数.

图8 孔压法测定Cv与logt法法计算值的比较
此外,研究连云港重塑土固结系数与竖向固结应力的关系还可发现,如图9所示,无论是基于孔压、时间对数法或时间平方根法计算得出的固结系数均随着固结应力的增大而增大,这表明在固结过程中固结系数并非常量,固结系数随着固结应力的改变而变化.

图9 连云港重塑黏土固结系数随固结应力变化关系曲线
4 结 论
针对连云港重塑黏土,采用Zeng等设计改进的能够测量试样底部孔压的渗透固结容器,进行一维固结压缩试验,探讨运用孔压计算土体固结系数的方法,并与传统计算方法进行比较:1)针对连云港重塑土进行一维固结试验,发现固结过程中试样底部孔压具有先增大后减小的规律,其峰值孔压滞后30min左右,约为荷载增量的一半.2)运用孔压法计算的固结系数Cv与时间对数法的计算结果接近,小于时间平方根法的计算结果,证明了孔压法计算结果的可靠性.3)试验发现针对连云港重塑土,无论是基于孔压、时间对数法或者时间平方根法计算得出的固结系数Cv均随着固结应力的增大而增大,表明在固结过程中固结系数并不是常数,而是随着固结应力的改变而发生变化.
[1] Taylor D W.Research on Consolidation of Clays[M].MIT publication,1942:82.
[2] Olson R E.Consolidation of Soils:Testing and Evaluation[J].Philadelphia:American Society for Testing and Materials,1986,892:7-70.
[3] Gibson R E.An Analysis of System Flexibility and Its Effect on Time-lag in Pore-water Pressure Measurements[J].Géotechnique,1963,13:1-11.
[4] Whitman R V,Richardson A M,Healy K A.Time-lags in Pore Pressure Measurements[J].Proc.5th ICSMFE 1,1961:407-411.
[5] Perlof W H,Nair K,Smith J G.Effect Ofmeasuring System on Pore Water Pressures in the Consolidation Test[J].Proc.6th ICSMFE,Montreal,1965(1):338-341.
[6] Robinson R G.Consolidation Analysis with Pore Pressure Measurement[J].Géotechnique,1999,49(1):127-132.
[7] Robinson R G.A Study on the Beginning of Secondary Compression of Soils[J].Journal of Testing and Evaluation,Sept.2003,30(5).
[8] Crawford C B.Interpretation of the consolidation test[J].J.Soil Mech.Found.Div.,ASCE,1964,90(5):86-102.
[9] Zeng Lingling,Hong Zhenshun,Cai Yuanqiang,et al.Change of Hydraulic Conductivity During Compression of Undisturbed and Remolded Clays[J].Applied Clay Science,2011,51:86-93.
