基于改进遗传算法的铁路三维空间线路智能优化方法研究

龙喜安

（中交第四航务工程勘察设计院有限公司，广东 广州 510230）

基于改进遗传算法的铁路三维空间线路智能优化方法研究

龙喜安

（中交第四航务工程勘察设计院有限公司，广东 广州 510230）

归纳和总结了铁路线路智能优化与三维空间信息之间的内在联系，基于OSG技术对空间信息数据进行高效组织，加工处理与信息输出为一体，建立了三维空间信息模型，为铁路三维空间线路智能搜索提供可视化地理信息环境。以平面交点坐标、交点半径、纵面变坡点里程、变坡点高程为设计变量，充分考虑了空间线路平面约束、纵断面约束、平纵组合约束和环境影响约束条件，深入分析铁路三维空间线路优化费用目标函数，建立了铁路三维空间线路综合优化数学模型。采用浮点编码方式，以交点偏移距、交点曲线半径、链式变坡点高程为基因序列，针对多约束条件构成的优化空间进行深入的研究，生成线路方案群；基于多目标排序矩阵方式对每代中线路方案进行适用度计算，设计了选择、交叉和变异三类遗传算子，逐代遗传进化，实现了线路方案向最优线路方案群自动搜索，完成了铁路三维空间线路智能寻优过程。以本文提出的理论与方法为基础，基于vs.net、OSG、数据库等技术实现了铁路三维空间智能选线系统的开发，结合实际工程对本文的理论模型与算法进行了验证和评价。

铁路选线；智能优化；改进遗传算法；空间信息模型；多目标；数学优化模型；

铁路三维空间线路智能优化是一个复杂的多目标优化问题，根据设计项目的功能需求，自动进行铁路三维空间线路搜索和结构物协调布设，搜索出线路、结构物与环境之间的最佳协调方案过程，具有降低铁路选线设计的劳动量与决策周期，提高选线工作效率与节约投资等重要意义。因此，开展铁路三维空间线路智能优化研究是当前发展的重要方向。

自60年代以来，国内外开展了线路优化方面的研究，国外学者对线路优化方法的总结如表1[1]所示。

纵观国内外研究成果，上述研究大多停留在了理论的层面上，提出的优化模型针对于实际情况均存在着不少缺陷，并没有真正的实用和推广开来，或者所提出的一些方法所产生的优化解，不具备实用价值。美国Maryland大学1998年Jong提出基于遗传算法公路空间线形优化模型[2]，初步应用于符合本国实际的较短线路优化中。

但是，由于各国线路设计标准与方式不同，并且进行线路设计的过程比较复杂，国外专家Jong所提出的公路三维空间路线优化理论与方法不能成功应用于我国铁路智能选线中，并且其优化模型存在如下缺陷：

1）模型中起点和终点之间划定等间距的若干切割面，形成的线路方案交点的个数与纵断面坡度中变坡点数目设为相同来考虑，造成平竖曲线重叠，与铁路线路设计标准规范不符；实际工程项目中纵断面变坡点数目与平面交点没有绝对的关系，变坡点一般不宜设置在平面曲线曲中点位置，竖曲线与缓和曲线不能重叠。

2）优化模型在基因的编码中，以各平面交点相对于航空线的偏移距和各平面曲线曲中点设计标高作为基因，形成染色体时，构成初始线路方案。但是，线路方案的形成中对铁路线路几何约束条件、环境影响约束条件、构造物约束条件（桥、隧、站），关联约束条件（与既有路网、水系、管道等线形构筑物交叉约束）考虑不全面。

表1 线路智能优化研究概况Tab.1 The research work of line intelligent optimization

3）Jong所提出的模型中以最小综合费用为目标函数，目标函数费用计算方式与铁路线路优化目标函数不同，综合费用计算方法不能直接运用于铁路线路优化模型，需要重新考虑铁路空间线路智能优化费用目标函数。

因此，目前国内外对铁路空间选线的智能优化方法还处在试验阶段，现有的关于铁路智能选线方面的研究还远远不够。在上述研究背景条件下，从深度和广度上开展该方面的研究具有重要意义。

1 线路三维空间信息模型与可视化优化环境

铁路线路三维空间信息模型是集三维空间选线相关信息的采集、高效组织管理、加工处理及实时动态的对相关信息进行调度与快速输出为一体的整体系统。将与铁路空间线路优化相关的信息进行分析，归纳并总结为空间地理环境信息、线路几何约束信息、线路构造物信息、关联约束信息四类。

空间地理环境信息包括数字地面模型，敏感区域信息等；线路几何约束信息主要是指线路几何设计标准；线路构造物信息主要包括桥梁、隧道与车站设置条件等；关联约束信息包括铁路线路与既有道路和桥梁立交，高程控制点选取，跨越水系等线形构造物等。

基于高性能跨平台三维渲染引擎（OSG）作为基础平台进行二次开发，解决铁路选线大范围区域信息处理，对地形、影像等海量地理信息数据进行建模并生成数字化地形模型，将各类空间信息数据有效进行整合，在该平台上研究并实现三维空间信息数据高效组织与管理、调度与信息提取等，构建线路三维空间信息模型，将各种信息与技术相集成，建立起可视化三维空间线路智能优化环境（图1）。

2 线路多目标优化数学模型

2.1 设计变量

铁路线路三维空间优化方案的设计变量可以归结为X,Y,R,K,H。其中

其中，m为平面交点个数，l为纵断面变坡点个数。

在铁路选线设计中，对于不同曲线半径条件下所对应的缓和曲线长度的选配具备固定要求，因此缓和曲线长度loi不作为设计变量。铁路等级确定以后，竖曲线半径为一固定值，所以竖曲线半径也不作为设计变量采用。

2.2 目标函数

目标函数主要包括建设工程费用，铁路建成以后的运营养护费及对环境影响的相关费用3个方面。

铁路工程基本建设费用（用C表示）重点可分为两类：①环境影响相关的各项工程经济费用与铁路线路上工程结构物基本建设费用CCΙ（Ⅰ类）；②铁路工程建设过程中基本设备各项费用CCΠ（Ⅱ类）。

式中：Δ为投资效果系数；C1为征地费用；C2为路基土石方工程费用；C3为桥梁建设工程费用；C4为隧道建设工程费用；C5为涵洞建设工程费用；C6为挡土墙建设工程费用；C7为房屋拆迁费用。

式中：Δ为投资效果系数；C8为线路轨道铺设所需要的工程费用；C9为防护栅栏设置所需要的工程费用；C10为铁路上各种信号设备购置费用之和。

运营费用主要包括设备购置成本、机车牵引能耗费用、养护维修费、管理费、折旧费用、旅客发送服务成本等。其中，牵引能耗费用、固定资产折旧与养护维修费用占用比例较大。

列车牵引计算是研究列车在各种外力作用下一系列与行车有关的运营、技术、经济指标的基础。其基本计算步骤[3]：三维空间线路确定条件下，对线路平、纵面设计数据进行提取与整理，将整条线路分为若干限制速度段，将每相邻两停车站之间的距离划分为计算单元，针对每一计算单元，依据最快速牵引策略每个分段上按照一定步长逐步递推计算各时刻的速度与位移。设列车运行中第j个计算单元中第i步的列车走行距离Sj,i，速度Vj,i，加速度aj,i，单位合力cj,i，纵面坡度ij。则第i+1步的递推公式如下：0k

图1 三维空间线路智能优化环境Fig.1 The environment of line intelligent optimization in three-dimensional space

其中：f(vt)为列车所受合力，a,b,c,k为常数；E为机车牵引能耗费用；Ck为养护维修费和管理费用。建立的综合考虑上述因素的目标函数为

其中：CCΙ(X,Y,R,K,H)为Ⅰ类建设工程费，CCΠ(X,Y,R,K,H)为Ⅱ类建设工程费，Co(X,Y,R,K,H)为建成后的运营费，CE(X,Y,R,K,H)为考虑环境影响的相关费用。

2.3 约束条件

2.3.1 平面约束

2.3.2 纵断面约束

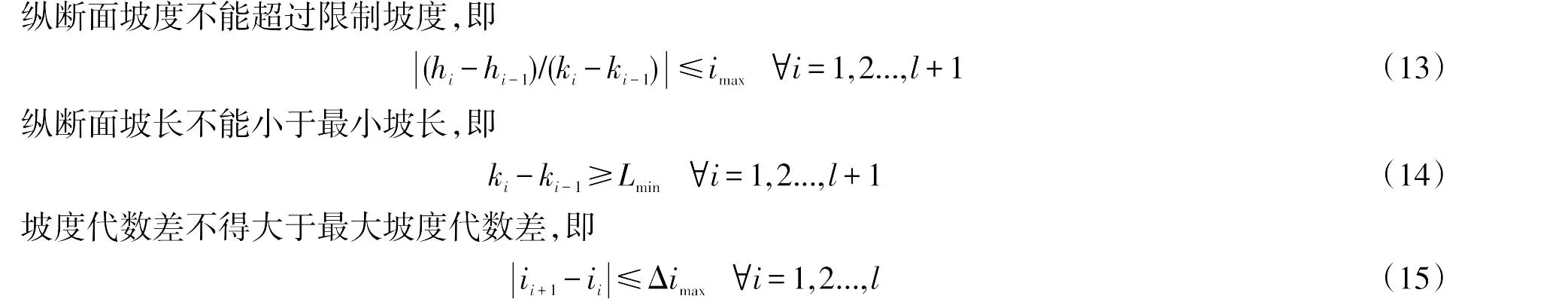
2.3.3 平、纵组合约束与环境影响约束

平纵组合约束同时影响平面和纵面设计参数的取值，主要包括:竖曲线与缓和曲线不重叠，坡度不大于曲线折减后的限制坡度等。

2.4 铁路三维空间线路优化模型

三维空间线路智能优化模型可表示为

该优化问题的求解，可表示为在满足全部约束条件下，不断寻找点(X*,Y*,R*,K*,H*)

使目标函数综合代价值在该点取得极小值，即对任意点

其中：平面几何约束个数为n，纵面几何约束个数为m，平纵组合约束个数为l，环境影响约束个数为t。

3 基于改进遗传算法的铁路空间线形优化

3.1 铁路线路三维空间基因编码

基于Jong[2,6-7]所提出的公路模型基础上，对线路三维空间基因编码进行改进，平面与纵断面控制点基因编码采用不同的分布，完成铁路线路三维空间基因编码，如图2所示。

图2 铁路三维空间线路模型Fig.2 Railway line model in three-dimensional space

点S(xs,ys,hs)和E(xe,ye,he)分别为线路的已知起点与终点坐标，线段SE为铁路线路起终点连线，O1,O2,O3,·······,On为线路起终点切割面。空间线路与切割面交点分别为p1,p2,p3,·······,pn；

空间线路在平面上进行投影时，切割面个数设为np，如图3所示；在纵断面上投影时，切割面个数设为nv个，np与nv数目不相同。空间线路在平面上进行投影时，将每个切割面定义为一维局部坐标系，向量SE在水平面上的投影与第i个切割面的交点oi设为坐标系的原点，pi在Oi平面内与原点之间的水平距离为di。

空间线路与垂直切割面在平面上投影时，交点坐标计算：

图3 铁路三维空间线路平面投影图Fig.3 The plane projection of railway line in three-dimensional space

其中：(xoi,yoi)每个切割面上坐标系原点，di为在i平面内与原点之间的水平距离，θ为切垂线在平面投影面内与x轴的夹角，计算如下；

在满足线路约束条件下，由pi(xpi,ypi),i=1,2,…,np形成交点数为m+2（包含已知起终点）的空间线路平面方案，经过考虑各种约束条件作用，切割面数目与平面交点数目并不一定相同，交点数目非均匀分布，结合各类约束条件进行了自动调整与分布。

第pi交点处半径为Ri，由半径取得该交点处缓和曲线长度为loi，转角计算为

进行平面曲线要素计算，分别计算出该交点处的切垂距mi，圆曲线内移量pi，切线长Ti，曲线长Li，外矢距Eoi，缓和曲线切线角βi。

对于纵断面设计变量，与平面投影线形模型相类似（如图4）；空间线路在平面上进行投影时，切割面个数设为np，纵断面切割面的间距dV可取合适的间距或者采用规范规定的最小坡长值，切割面总数为nv，与平面切割面个数不同，一般大于平面切割面总数，各切割面与三维空间线路的交点Pi(i=1,2,…,nv)，高程赋值通常采用如下三种赋值方式。

以Pi(i=1,2,…,nv)为纵断面初始变坡点，形成链式坡；变坡点里程ki(i=1,2,…,nv)可通过三维空间线路与纵面切割交点Pi(i=1,2,…,nv)在平面上投影求出，高程为hi(i=1,2,…,nv)。

第二中赋值方式为：对每个变坡点处先形成区间[hiL,hiU]，在该区间内产生合理的高程，为了使形成方案满足纵面约束要求，区间取值计算方法如下

第一种较为简单的赋值方式可以用如下公式计算

即hi(i=1,2,…,nv)赋值方式可为hi=rd[hiL,hiU]，或者预先内插出Vi处的地面线高程hg(i)，若hgi大于hiU，hi=hiU，若hgi小于hiL，hi=hiL;hiL＜hgi＜hiU,则hi=hgi若线路行经方案区有高程控制点、跨越水系，道路时，[hiL,hiU]取值范围进行相对应调整。

对于缓坡地段，在纵断面生成方案中，可以考虑以土方填挖高平衡，使工程费用最省为目标的方式确定变坡点高程，考虑应用如下第三种赋值方式。

设Vi(ki,hi),Vi+1(ki+1,hi+1)为第i坡段的两变坡点，Vi(ki,hi)点高程已求出，该坡段内生成m个地面线桩号，其中第j个桩号处里程和地面高程分别为kEj和hEj。该坡段的坡度iP满足

图4 铁路三维空间线路纵断面投影图Fig.4 The profile projection of railway line in three-dimensional space

综合考虑土方填挖平衡，线路约束条件等因素，对纵断面约束条件进行检验，纵断面坡长与标高进行调整，形成最终纵断面方案，纵断面变坡点里程向量可表示为K=[ ]k1,k2,…,kl

采用浮点编码方式，以空间线路与切割面（在平面上进行投影）交点Pi(i=1,2,…,np)相对于航空线的偏移距di(i=1,2,…,np)，半径ri(i=1,2,…,np)，缓长li(i=1,2,…,np)为基因编码，以空间线路与切割面（在纵断面上进行投影）交点Pi(i=1,2,…,nv)高程hi(i=1,2,…,nv)则作为遗传算法的另一部分基因编码，Λ为染色体，λi(i=1,2,...,n)表示基因，线路三维空间染色体表示：Λi=[λi,1,λi,2,...,λi,n]=[di,1,di,2,...,di,np,ri,1,ri,2,…ri,np,li,1,li,2,…li,np,hi,1,hi,2,....hi,nv]由上述可知，染色体中的基因由平面交点基因片段di,1,di,2,...,di,np，半径基因片段ri,1,ri,2,...,ri,np，缓长基因片段li,1,li,2,…li,np和纵面基因片段hi,1,hi,2,....hi,nv四部分组成。

3.2 基因调整与线路方案形成

线路三维空间线路方案形成过程受约束影响，需对线路方案进行约束条件检测，针对局部出现的未满足约束条件的基因区段，需提出相应的调整策略，进

行

相对应的自适用基因调整与改进[8]；如图5所表示。约束检测过程中，针对局部基因区段位于禁止穿越区内时，应及时对该基因片段自动调整，使其取值不处于该区域内，生成的线路方案满足约束要求。

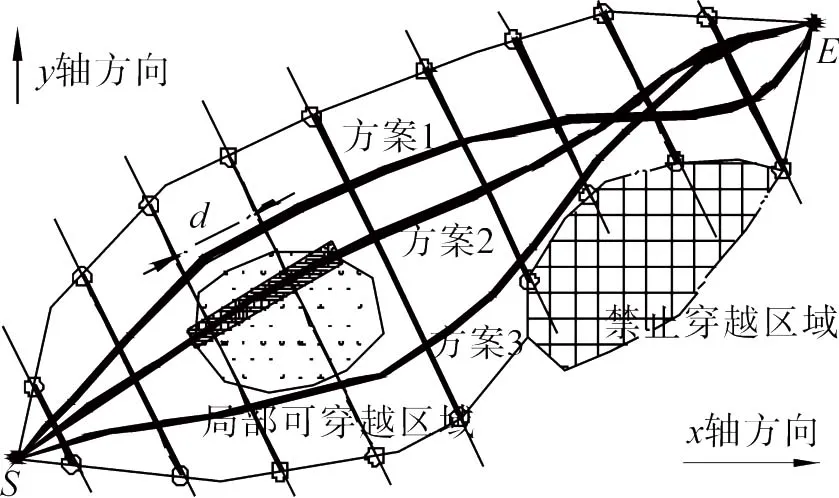
图5 平面控制区域约束图Fig.5 The constraint graph of plane control area

3.3 适用度的确定

基于多目标排序矩阵[5]对每代中每个方案进行适用度的计算，利用自适用度变化调整的方式确定交叉和变异概率，控制种群中线路方案并行向最优线路方案群靠近。

设种群中个体的个数为m，记为Rj(j=1,2,···,m)，Rj为种群中第j个个体；目标函数的个数为n，记为Ci(i=1,2,···,n)，Ci为第i个目标函数。种群中所有线路方案对其中某一个目标函数代价值由低至高（方案由从优到劣）排序,每个线路方案得到的序号值记为Xi=[xi,1,xi,2,xi,3,······,xi,m-2,xi,m-1,xi,m] ，将种群中所有线路方案依次对每一个目标函数Ci(i=1,2,···,n)进行代价值排序，目标函数的表现矩阵X=[X1,X2,X3,······,Xn-2,Xn-1,Xn]T，其中n为目标函数个数，如下所示：

其中：X为n×m阶矩阵，xn,m表示种群中第m个线路方案针对第n个目标函数代价值进行优劣排序以后得到的序号值。

设种群中所有线路方案对其中某一个目标函数Ck适用度值计算

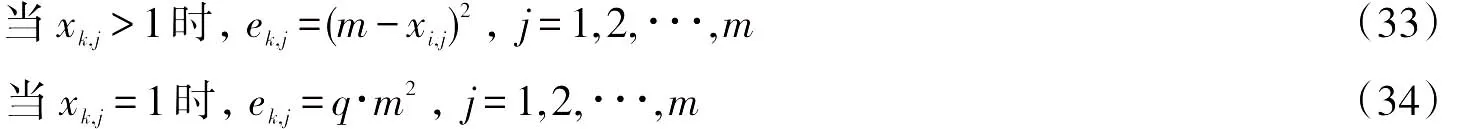
其中：m为种群中方案个数，k表示某一个目标，j表示种群中某个方案。ek,j表示种群中第j个方案对目标k的适用度值，q为区间(1,2)之间的常数，用于表示个体方案表现最优时，加大其适用度值。记为

其中：E为n×m阶矩阵。种群中每个方案对所有目标函数的综合适用度值计算可表示为

3.4 遗传算子设计

遗传算子设计包括线路方案选择、交叉与变异三种类型，是决定遗传算法实施效果的关键[9-11]。

3.4.1 交叉操作

基于多种改进的交叉运算，进行铁路三维空间线路进行全局搜索，维持线路方案群群体的多样性，成功避免了优化过程中早熟的产生。主要包括单点交叉，多点交叉，算术交叉与启发式交叉。

单点交叉是通过交换三维空间线路方案中的单个基因（即为线路中的单个交点）来完成交叉全过程。设Λi,Λj为拟进行交叉的父方案，即

首先确定产生进行交叉的平面基因位置，同时找出该交点对应纵面链式坡基因发生变化的片段位置v1,v2，且v2＞v1；交换相对应平面基因和纵面基因，形成两个新的子方案；即

算术交叉通过采用一定比例系数对所有基因进行组合完成交叉全过程。设Λi,Λj为拟进行算术交叉的两个父方案,同上式（38）和（39）；随机产生进行算术交叉的以参数ω=rd[0,1]，将平面基因与纵面链式坡基因同时进行交叉，形成两个新的子方案；即

形成的两个均应满足约束条件要求，即

启发式交叉通过对所有基因进行线性组合来完成交叉过程。同时设计非均匀启发式交叉算子，以平面交点基因片段为基本单元，确定该交点对应的三维空间基因的进化方向。

设Λi,Λj为拟进行启发式交叉的两个父方案，同上式（38）和（39）；随机产生进行启发式交叉的以参数ω=rd[0,1]，当父方案Λi比父方案Λj优时，产生新的子方案Λ'的计算方式为

整个方案的优劣确定统一的进化方向

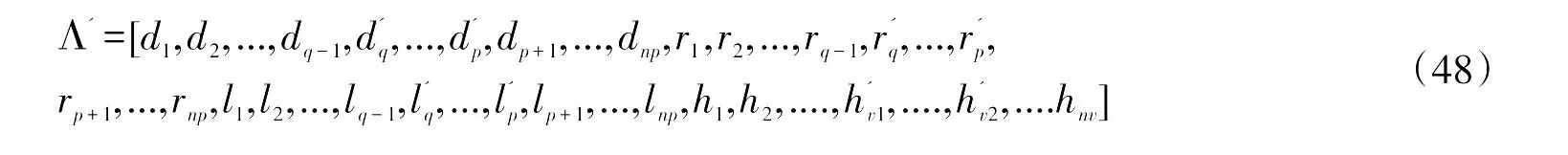
反之亦然。

3.4.2 变异操作

变异操作在遗传算法中是产生新的线路方案的辅助方法，可提高算法对整个空间的局部搜索，通过交叉与变异操作相互配合，对三维空间线路方案完成良好的全局搜索与局部搜索。

均匀变异中有利于将个体方案中穿越禁区或者高费用敏感区域的基因片段进行变异，避免线路穿越。设Λi为拟进行均匀变异的某个父方案

选择需要进行变异的平面基因位置，设随机选择的平面基因位置位于禁区内，然后用随机产生的浮点

部分基因片段的优劣确定进化方向数d'i,p给予替换，并对染色体进行扩展可得产生两个独立变量a,b分别将a至p，p至b之间的基因发生均匀变化，可得

将平面基因起终点移除，变化的平面基因片段所对应的纵面链式坡基因片段也相应发生了变化，设纵断面基因变化的片段位置v1,v2，且v2＞v1；(v1,v2)区间内纵面基因片段的生成可按照初始种群形成过程中纵面链式坡基因生成的原理进行类似处理，形成新的子方案Λ'i为

采用直线变异的方式进行变异，以平面交点为基本单元，有利于对穿越高费用敏感区域的基因片段进行变异，设Λi为拟进行直线变异的某个父方案，产生两个独立变量a,b

其中a与b不相等，并且a小于b，分别将a至b之间的平面基因发生直线变异

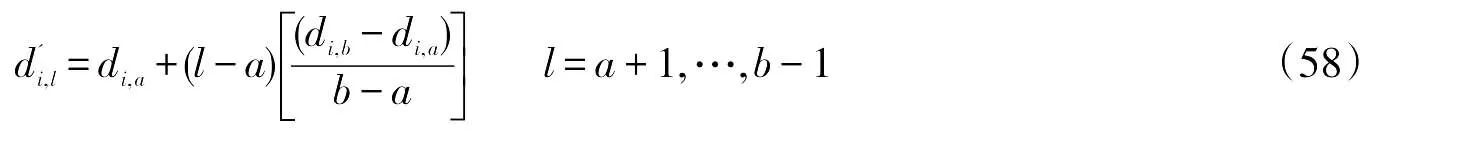
直线变异的平面基因片段所对应的纵面链式坡基因片段也相应发生了变化，设纵断面基因变异的片段位置v1,v2，且v2＞v1；即

非均匀变异的主要特征为随着线路方案更优，单个交点产生变异的幅度值越小，变异不明显，主要针对走廊带区域已优化确定条件下，对线路方案进一步产生微调的效果，使其更优而设计。设di,k为拟进行非均匀变异的某个父方案Λi中第k个平面基因，随机产生一个整数r，取值为0或者1，产生变异的方式为

其中：dmax，dmin为平面第k个基因取值的范围。

式中：t表示当前遗传进化的代数；n表示进行优化的总代数；ε为变异参数。

4 系统的开发应用

基于vs.net、OSG、ARX等技术进行铁路三维空间智能选线系统的开发，选取某地区地形条件下某铁路为例，进行铁路线路的智能优化选线，该地段人工设计线路长约为18 km。该地段铁路等级为Ⅱ级铁路，选线设计主要技术标准如下表2所示。

表2 某线路智能优化主要技术标准Tab.2 The main technical standards of line intelligent optimization

初选智能优化控制参数设置如表3所示，起终点坐标设置为起点(13 589 692.1，2 370 032.05，393），终点（13 602 166.344，2 359 424.497，318）；

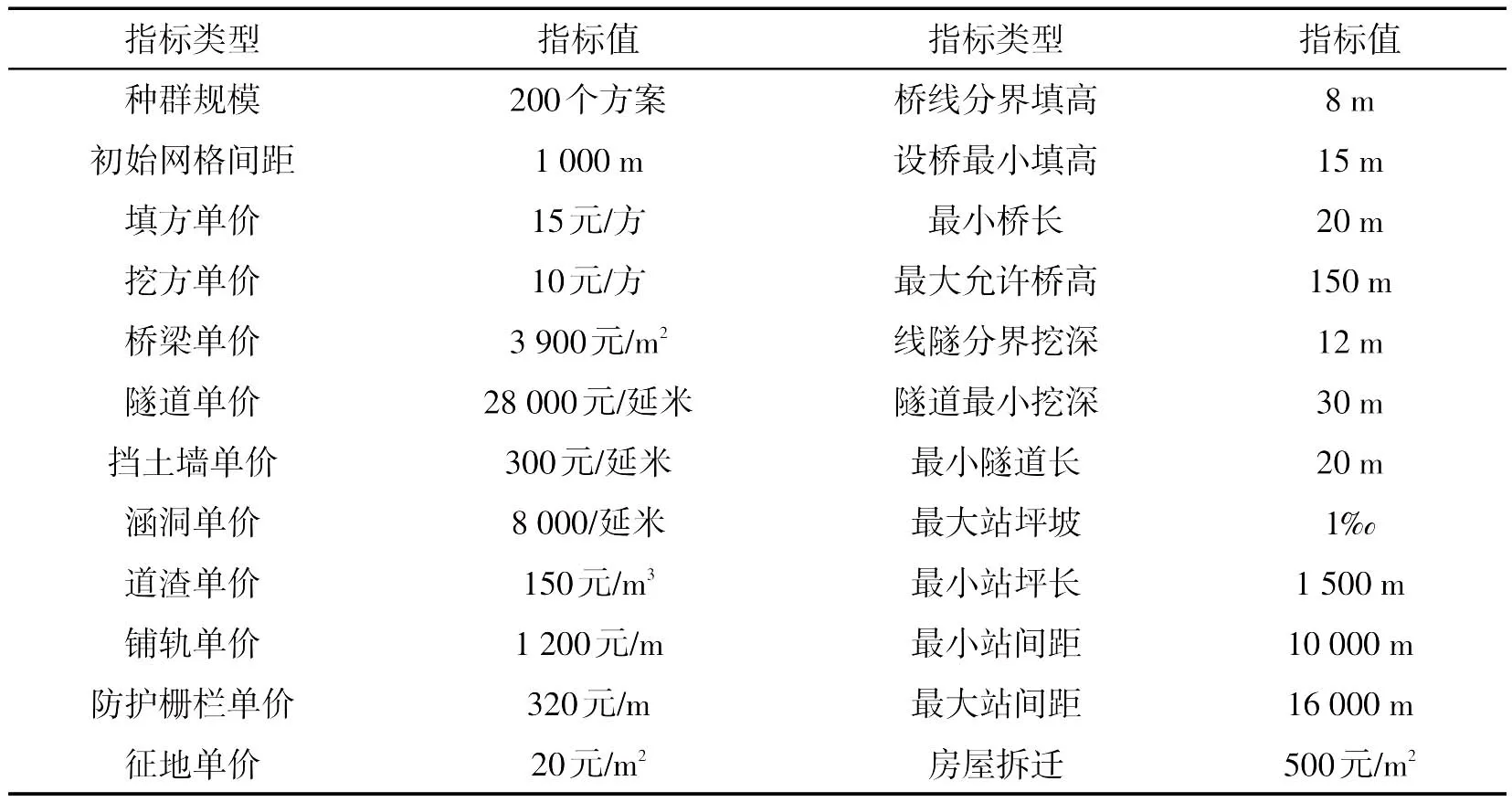
表3 某线路智能优化控制参数设置Tab.3 The control parameters of line intelligent optimization

智能优化选线在惠普Z600工作站（4核2.13 G CPU，4 G内存，500 G硬盘）上进行，搜索范围为22 km×16 km的矩形区域。方案搜索过程中，针对每一代中所有线路方案进行目标函数代价值计算，并将计算方案从优至劣进行排序，保存每一代中前10个最优线路方案，便于对每代最优方案进行对比分析。

通过对该算例进行搜索可知，迭代优化进行至80代以后，线路目标函数代价值变化相对稳定，并且变化幅度越小，线路方案代价值保持在51 182万元左右，接近于最优线路方案。进化至92代收敛，累计耗时约124分钟，得到最优线路方案群，智能优化最优方案工程代价值约为51 151.941 8万元，搜索方案最优线路方案群与人工设计方案平面图如图6所示。

图6 最优线路方案群与人工设计方案Fig.6 The optimal route plan group and the artificial scheme

如上图可知，搜索最优线路方案为了更好的适用地形起伏变化，方案中坡段数较多，方案较为合理，在该系统下将搜索的最优方案与人工选定线路方案进行对比，如表4所示。

表4 实际方案与人工选线方案对比Tab.4 The comparison of the scheme between actual line selection and artificial line selection

由对比表可见，智能选线方案线路里程长度比人工选线长度短，土地征用、填土方、挖方、植草等较人工方案更为节省；人工设计方案中出现了两条隧道，智能优化方案中没有出现隧道，降低了工程造价费用；计算可知，智能优化方案总节省费用约为3 907.539 5万元，总费用投资节约率约为7.096 9%。

5 结论

1）首先通过对国内外文献资料的阅读归纳和总结了与铁路空间线路优化相关的空间信息类型，提出了空间信息数据的挖掘与表达方法，基于OSG对空间数据进行高效组织、加工处理与信息输出为一体，建立了三维空间信息模型，为铁路三维空间线路智能搜索提供可视化地理信息环境。

2）其次对铁路空间线路优化数学模型的构建理论与方法进行了研究。以线路平面交点坐标、平曲线半径、纵面变坡点里程、变坡点高程为设计变量，充分考虑线路平面约束、纵断面约束、平纵组合约束和环境影响约束的作用，较为全面的考虑了铁路三维空间线路优化费用目标函数，建立铁路三维空间线路优化数学模型。

3）再次还基于改进遗传算法进行铁路三维空间线形的优化。采用浮点编码方式，以交点偏移距、交点半径、缓和曲线长度、链式变坡点高程为基因序列，进行了三维空间基因编码，在约束空间下生成线路方案群，对不满足约束条件的方案进行自动调整，设计出可考虑各类约束条件的遗传算子，逐代遗传进化，优化出最优线路方案群。

4）最后以理论与方法为基础，基于vs.net、ARX、数据库等技术进行了三维空间智能优化系统的开发，最终结合实际工程算例对本文的模型与优化算法进行了验证和评价。

[1]KIM E,JHA M K,SON B.Improving the computational efficiency of highway alignment optimization models through a stepwise ge⁃netic algorithms approach[J].Transportation Research,PartB,2005,39(4):339-360.

[2]JYH CHENG JONG.Optimizing highway alignments with genetic algorithms[D].College Park:University of Maryland.1998.

[3]蒲浩,李伟,龙喜安.高速铁路牵引计算与三维运行仿真研究[J].铁道科学与工程学报,2011,8(5):1-5.

[4]后宗彪.费用现值目标函数铁路主要技术标准综合优化[D].成都:西南交通大学，2006.

[5]游进军，纪昌明，付湘.基于遗传算法的多目标求解方法[J].水利学报;2003(7):64-70.

[6]KANG M W,JHA M K,SCHONFELD P.Applicability of highway alignment optimization models[J].Research,Part C,2012,21:257-286.

[7]KANG M W.An alignment optimization model for a simple highway network[D].Maryland:University of Maryland,2008.

[8]KANG M W.Prescreening and repairing in a genetic algorithm for highway alignment optimization[J].Computer-Aided Civil and Infrastructure Engineering,2009(24):109-119.

[9]JHA M K,KIM E.Highway route optimization based on accessibility,proximity,and land-use changes[J].Journal of Transporta⁃tion Engineering,2006,132(5):435-439.

[10]KIM.Intersection modeling for highway alignment optimization[J].Computer-Aided Civil And Infrastructure Engineering,2004,19:119-129.

[11]王顺利,王正彬,陈东.铁路枢纽客运站布局优化研究[J].华东交通大学学报，2013,30(1):71-75.

Intelligent Optimization of Railway Lines in Three-dimensional Space Based on Improved Genetic Algorithm

Long Xi’an
（CCCC Fourth Harbor Engineering Investigation and Design Institute Co.,Ltd.，Guangzhou 510230，China)

The internal relationship between the railway line intelligent optimization and three-dimensional geo⁃spatial data is szcmmarized.Based on OSG,it firstly establishes the three-dimensional spatial information model by organizing,processing and outputting the spatial data as a whole,which may provide visualization of geographi⁃cal information environment for searching the railway line schemes in three-dimensional space.Then,it analyzes the cost objective function of the railway lines and builds up the comprehensive optimization model for railway line intelligent optimization in three-dimensional space.Besides,it calculates the applicability of line schemes based on multi-objective sorting matrix and designs the genetic operators of selection,crossover and mutation.The line schemes to be near the group of optimal route scheme is realized by genetic evolution.And railway line intelligent optimization in three-dimensional space is completed by searching performance,forming the group of optimal and valuable line schemes.Based on the theory and method which are proposed,the intelligent line selection system in three-dimensional space is realized based on the technology of vs.net,OSG,database technology,etc.Finally,the verification and evaluation of theoretical model and algorithm has been carried out by using the practical engineer⁃ing projects.

railway location;intelligent optimization;improved genetic algorithm;spatial information model;multi-objective;mathematical optimization model

U212.3

A

1005-0523（2014）02-0048-14

2013-11-05

龙喜安（1987—），男，工程师，硕士，主要研究方向为道路与铁道工程勘察与设计、机场与港口路基路面设计。

book=61,ebook=102