铁路信号继电器触簧系统冲击特性应用研究

曹云东，孙宏杰，王贝贝，刘 炜

(1.沈阳工业大学，辽宁沈阳110000;2.沈阳铁路信号有限责任公司110000)

1 引言

铁路信号继电器是铁路运输信号控制的基础元件，无论是作为继电式信号系统的核心部件，还是电子式或计算机式信号系统的接口部件，在保障铁路信号系统安全性和可靠性方面都发挥着重要作用。由于其结构的特殊性(主要体现在触簧系统中簧片形变和触头接触都具有的高度非线性特征)和重要性，其抗振性和抗冲击性设计一直是耐环境设计中的重点和难点。继电器在机械振动与冲击的工况下，机械过载时将引起继电器闭合触点“抖断”或断开触点“抖闭”的失效模式，发生触点微动磨损，严重时甚至会造成触点误动作及机械构件疲劳断裂的现象。

国内外针对继电器的冲击特性的仿真研究较少［1.2，3］，大多数是产品验证试验，主要由于冲击触头接触高度的非线性和冲击作用的瞬时特性，采用传统算法并不能保证每个时间步的能量守恒，因此采用传统的时间积分算法显然不能得到良好的冲击特性。美国麻省理工学院提出的Bathe复合隐式时间积分算法，保证了求解时每个子步内能量守恒，能获得稳定的数值解［4，5］，并做了推理和实例验证。本文在总结了现有研究成果的基础上，建立了具有刚柔耦合结构的触簧系统等效冲击特性物理模型，将Bathe复合时间积分算法用于非线性接触和冲击问题的求解，探索了铁路信号继电器冲击特性问题求解的新途径。

2 触簧系统物理模型

针对铁路信号继电器受到冲击作用时最容易发生冲击形变的触簧部件，考虑到簧片形变和触头接触非线性的影响，建立了铁路信号继电器一组触簧系统的冲击特性物理模型，如图1所示。考虑到建模分析需要，采用等效力代替拉杆的作用。继电器动作时，推动杆给动簧片施加一个推动力F带动动触头运动，使动、静触头接触到达平衡位置，完成继电器触簧系统的闭合过程，然后根据振动传递路径，在底座施加冲击激励。

冲击非线性动力学平衡方程:

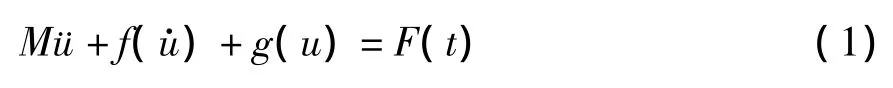
式中，M为质量矩阵;f(u·)为阻尼力;g(u)为恢复力;F(t)为冲击作用力;ü为节点加速度向量;u·为节点速度向量;u为节点位移向量。

在受到冲击作用下，动簧片和静簧片会发生非线性抖动形变，动触头与静触头接触力随着簧片形变不断发生变化，而底座固定受到冲击不会发生变形，但冲击作用力会通过底座传递到簧片使簧片发生形变。另外，由于冲击的短时瞬态性，决定了触簧系统具有高度非线性和刚柔耦合特性。如何能保证求解步内能量守恒和高效的求解精度，得到准确的冲击特性，求解积分算法成为了关键因素。为此，本文采用Bathe复合时间积分算法求解触簧系统的冲击特性。

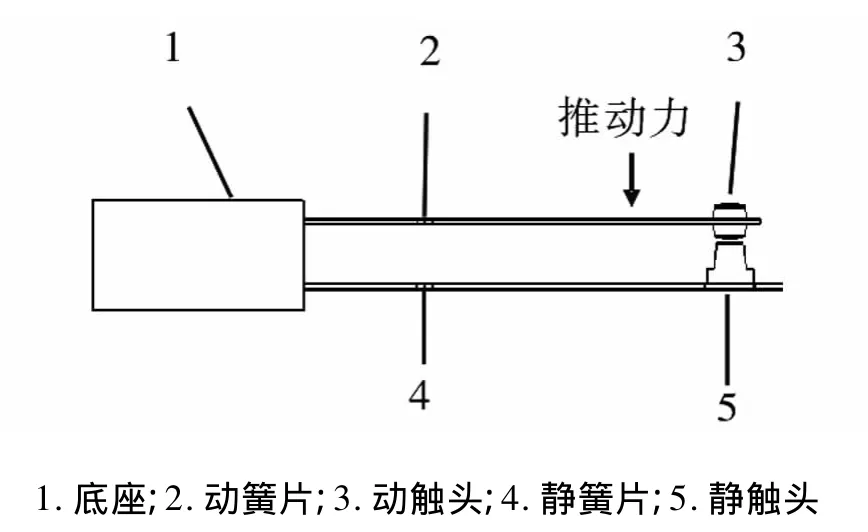
图1 触簧系统模型

3 Bathe复合时间积分算法

Bathe隐式复合时间直接积分方法进行系统迭代求解的基本思想是引入系数γ∈(0，1)，将时间步t到t+Δt分成两个时间段，分别为 和 。Bathe复合时间积分算法采用二阶隐式格式，在每个时间段内把梯形格式和三点向后差分格式有效的结合起来，进行迭代求解，而且，Bathe复合时间积分算法求解非线性问题时能保证每个时间步的能量守恒［4］，因而将Bathe时间积分算法应用到求解继电器冲击问题时，引入很小的耗散，能更好的反映结构对瞬时冲击载荷的响应，能得到准确的冲击特，有效地解决了接触非线性与短时冲击求解计算时振荡失稳和能量不守恒的问题。

联立式(2)～(4)可以得关与位移变量t+γΔtu·的Newton－Raphson迭代求解格式

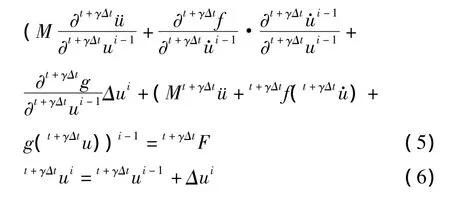
任意函数h在t+Δt时刻的导数可由其在t与t+γΔt时刻的函数值表达为:

对于t+Δt时刻系统平衡方程，联立上式可得关于位移变量t+Δtu的 Newton－Raphson迭代求解式:

针对本文冲击抖动接触问题的特殊性，当选取合适的γ时能保证引入的耗散最小，能准确地反映结构对瞬时冲击载荷的响应。

4 冲击动态计算

根据实际情况，在触头运动方向施加冲击激励信号对触簧系统的影响最大。因此，按照GBT 6902－2001铁路信号继电器试验方法标准，在底座施加如图2所示的半正弦冲击激励，脉冲信号持续时间为18ms。

图2 冲击激励信号

当沿触头运动正方向施加冲击激励信号时，进行冲击特性计算，得到如图3(a)所示的接触力变化曲线。

图3 (a)推动力为0.5N时正向冲击接触力曲线

当沿触头运动负方向施加冲击激励信号时，进行冲击特性计算，得到如图3(b)所示的接触力变化曲线。

通过图3(a)和3(b)可知，当施加正向冲击信号时，接触力按照正弦曲线增加，随后衰减震荡至稳定值，此时不会发生抖断现象;当施加反向冲击信号时，接触力按照正弦曲线减小，随后衰减震荡至稳定值，容易出现抖断接触力为零的现象，因此选取反向施加冲击信号进行计算，并以此接触力曲线作为触点是否发生抖断的判别依据。

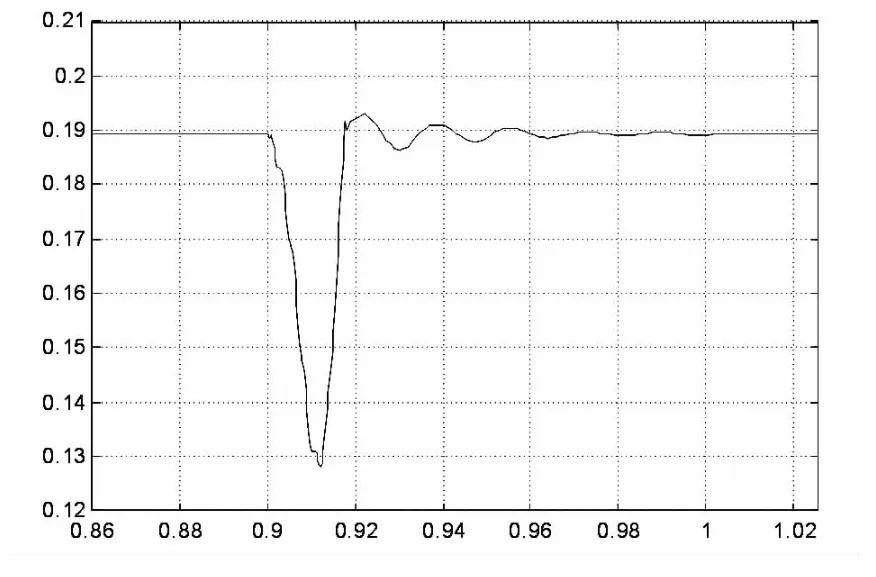
图3 (b)推动力为0.4N时反向冲击接触力曲线

5 实验研究

实验采用G系列振动实验系统，调节上位机控制振动台施加响应的冲击信号激励进行冲击实验，实验过程中通过监测触点间的电压作为触头接触状况的判据，冲击试验平台如图4所示。利用上位机对触点的状态和振动台进行控制。

图4 冲击实验平台

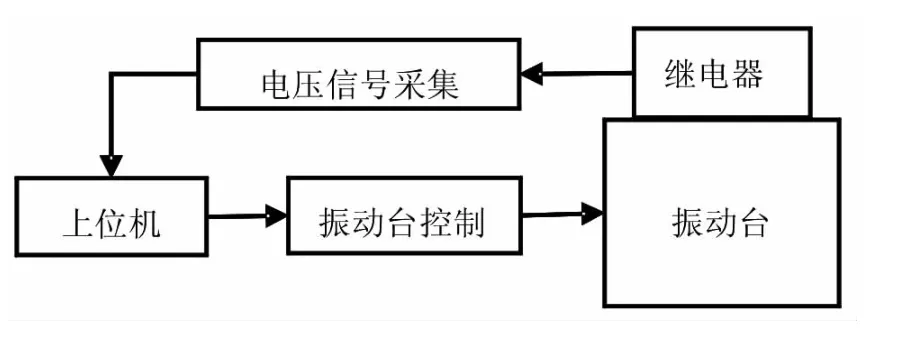
图5 冲击试验系统

实验中通过上位机调节参数施加如图2的冲击信号，并根据触头接触情况不断调节冲击加速度峰，经过实验研究，冲击信号的加速度峰值小于463时，触头电压没有陡增，触头可靠接触。触点电压信号如图6(a)所示;

图6 (a)触头无抖断电压波形

当冲击信号加速度峰值为463时触点发生抖断，触点间电压经过放大出现23.5V左右脉冲电压如图6(b)所示。

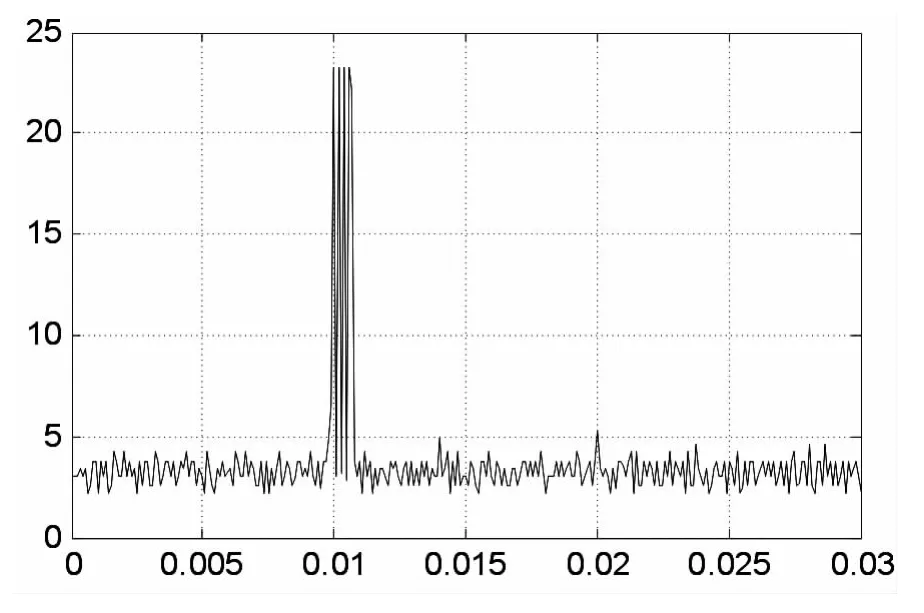
图6 (b)触头发生抖断电压波形

6 实验与计算结果分析

本文采用Bathe复合时间积分算法进行冲击特性分析，根据触点接触力的变化曲线作为触点是否发生抖断的判别依据，计算结果与实验分析对比如表1所示。

通过实验验证采用Bathe复合时间积分算法求解冲击和接触问题，很好地反映出冲击瞬时效应，克服了传统算法求解失稳发生震荡的现象，求解结果具有很高的准确性和可靠性。

表1 实验与计算结果对比

通过改变推动力的大小可以实现对初始接触力的调节，不断提高冲击加速度的峰值可以得到极限冲击加速度的临界值。

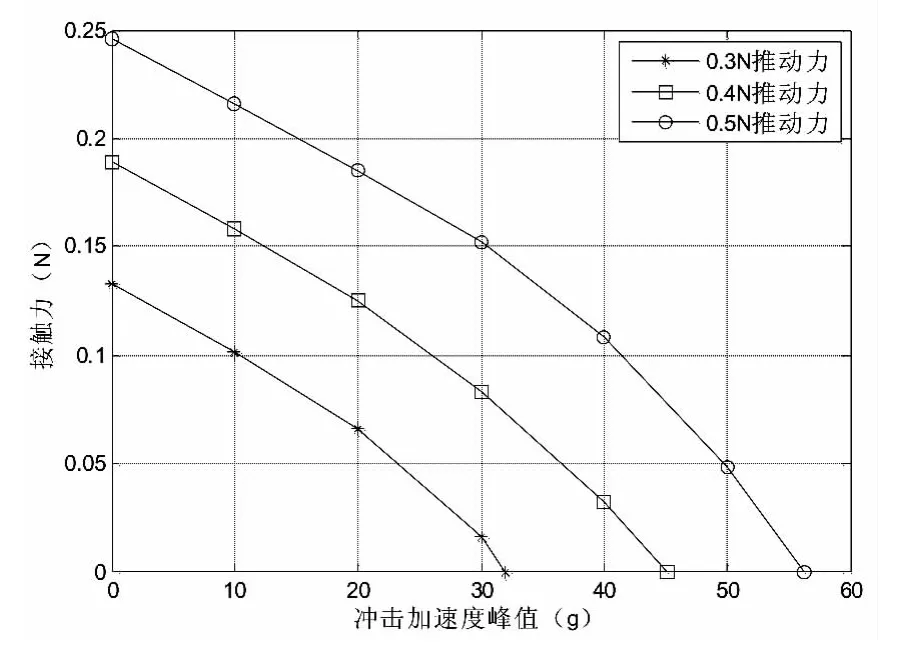
图7 接触力与冲击加速度关系曲线

从图7和8中我们可以看出，推动力越大导致初始接触力越大，承受的冲击极限加速度越大，系统越稳定，抗冲击性能越好;在同一推动力作用下，系统处于较低的冲击加速度峰值时，接触力随冲击加速度峰值增大线性下降;当冲击加速度峰值不断增大，接触力急剧下降，接触力变化呈非线性变化;不同推动力作用时，推动力越大，接触力线性段下降区域越长，接触力下降的比较缓慢。

图8 接触力、推动力与冲击加速度关系曲线

7 结论

(1)本文建立了铁路信号继电器触簧组的刚柔耦合的物理模型，将Bathe复合时间积分算法应用到继电器冲击动态特性求解，并通过试验进行验证，本研究方法对于冲击接触这类高度非线性的问题具有很高的准确度和可靠性，克服了传统算法求解瞬时冲击响应时发生震荡失稳的缺点，并且能够保证收敛过程中每个子步的能量守恒，得到了铁路信号继电器比较准确的冲击特性;

(2)通过分析可知，初始推动力越大，系统可承受的冲击峰值越大，抗冲击性能越好;在同一推动力作用下，接触力随冲击加速峰值增大呈两段式下降，冲击加速度峰值较低时，接触力呈线性变化;冲击加速度峰值较大时，接触力呈非线性变化;且推动力越大，非线性段持续的时间越长。

(3)本文为解决短时冲击和接触高度非线性这类难题提供了一种有效地方法，具有重要的研究价值。

［1］ Dominic J Chambega.A qualitative analysis on the effect of external vibrations on the performance of relays.IEEE AFRICON4th，1996;(2):1035 －1039

［2］ ［苏］罗依金.小型密封电磁继电器.王蓉芳译.北京:人民邮电出版社，1979:81－82

［3］ 翟国富，任万滨，许峰，等.电磁继电器触簧系统振动极限加速度的分析方法［J］.振动工程学报，2004，17(1):66－71.

［4］ K J Bathe，M Baig.On a composite implicit time integration procedure for nonlinear dynamics［J］.Computers ＆Structures.2005，83:2513 －2524.

［5］ K J Bathe.Conserving energy and momentum in nonlinear dynamics:a simple implicit time integration scheme［J］.Computers＆Structures.2007，85:437 －445.

［6］ 焦常科，李爱群，王浩.非线性阻尼动力方程的复合积分法［J］.力学与实践，2010，32:66 －70.

［7］ 宋宇，曹树良.复合隐式时间积分格式的非线性问题仿真研究［J］.计算机仿真.2012，11:180－184