MTF曲面构造方法研究

朱近

（南京理工大学计算机科学与工程学院，南京 210094）

0 引言

调制传递函数（modulation transfer function，MTF）是反映成像系统在对目标物成像过程中信号扩散与衰减程度的函数[1]。MTF以空间频率的函数形式存在，其值的大小反映了光学成像系统的清晰度，是客观表示像质的一个重要指标，并可以扩展到成像过程的各个环节。

假定成像系统具有线性及空间不变性的特点，而MTF是定义在二维空间频率域的实函数，因此可以用一个空间曲面——MTF曲面来描述。在数字成像系统中，MTF二维曲面常用一个MTF矩阵来近似表示。在航天相机系统设计、成像系统品质评价、遥感影像复原等领域[2-4]，准确估算MTF曲面是研究工作的前提。但成像系统MTF曲面不能直接通过测量获得，需要对几个特定方向进行测量，以获取各方向的一维MTF曲线[5-6]，再由这些特定方向的一维MTF曲线构造二维的MTF曲面[7-9]。

本文对现有的构造MTF曲面方法：乘积法和插值法进行分析，提出一种利用多个方向的一维MTF曲线绕中心轴旋转生成MTF曲面算法：旋转插补法。采用（准）高斯函数和4次多项式函数作为二维MTF曲面的模拟标准，对上述各方法的有效性和误差分布进行定量分析。

1 二维MTF曲面构造方法

一维MTF是一条随频率变化的单值连续曲线[10]，其横坐标为频率u，以截止频率作为基准对频率坐标做归一化处理，取频率区间u∈[–0.5,0.5]，u=0.5处称为Nyquist频率；纵坐标为MTF值。曲线MTFu(u)＞0与原点对称，归一化处理后在0频(u=0)处取最大值，MTFu(0)=1。

设空间频率坐标系为UOV，二维MTF曲面MTFuv(u,v)应具有性质：

1）在u,v∈[–0.5,0.5]，MTFuv(u,v)是单值、连续的；

2）MTFuv(u,v)≥0，归一化处理后在原点取最大值MTFuv(0,0)=1；

3）由于模的对称性，MTF曲面与原点对称。

因此，本文对MTF曲面的推导计算均在第I象限进行，由对称性可方便地推广到其他3个象限。目前常用的由多个特定方向的一维MTF曲线，建立二维的MTF曲面的方法包括乘积法和插值法。

1.1 乘积法

已知U、V两个特定方向的MTF曲线分别为MTFu(u)和MTFv(v)，则二维MTF曲面的表达式为[6]

用对称于原点的二维高斯函数模拟MTFuv(u,v)曲面为

式中σ1、σ2为U，V方向的尺度参数；ρ为相关系数。

根据二维概率分布函数的定义，当参数ρ=0时，MTFuv(u,v)函数曲面独立，为

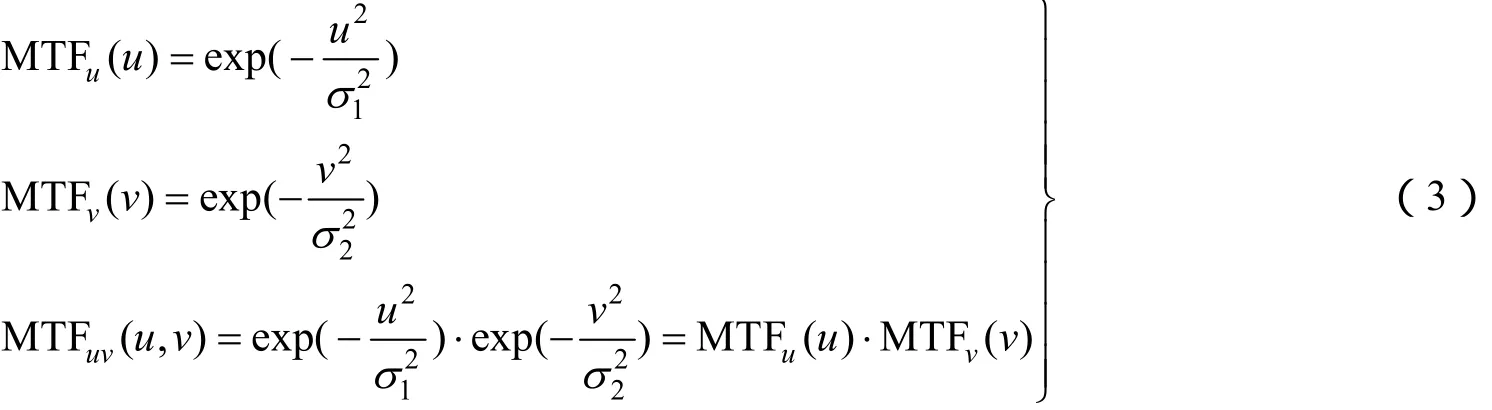
此时的MTFuv(u,v)函数曲面如图1所示，满足MTFu(u)=MTFuv(u,0)，MTFv(v)=MTFuv(0,v)；可用式（1）的计算结果精确构建对应的二维MTF曲面。

在实际成像系统中，二维MTF曲面一般不满足独立性要求[6]。用式（1）构造的二维MTF曲面在±45°方向边界上的值会出现与常规MTF曲面不一致的局部极小现象[3]。

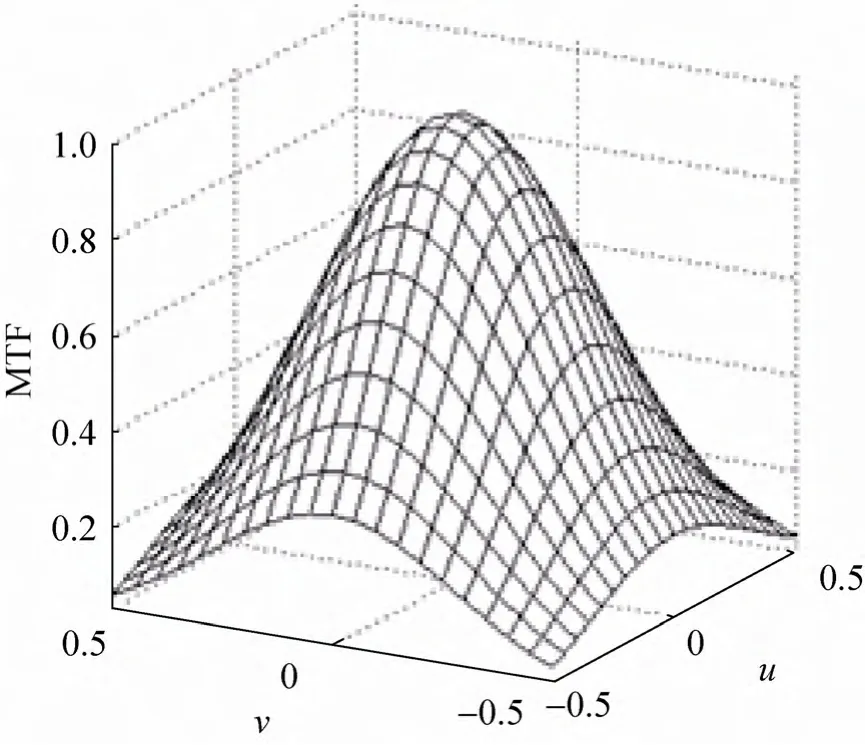
图1 二维高斯曲面Fig.1 2-D Gaussian surface

1.2 插值法

为了弥补乘积法的缺陷，文献[3]提出了一种使用二维插值构造MTF曲面的方法，经推导整理得到计算步骤为：

但在实际计算中，往往无法获得真实的45°方向MTF曲线，文献[4]提出了一种估算MTF45°(0.5)的经验公式，即：

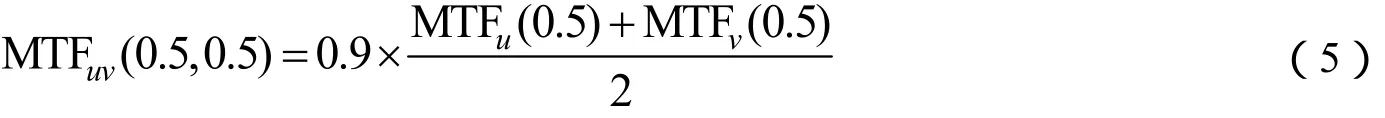
2）根据U方向的MTF向量之间的比例关系进行一维插值：

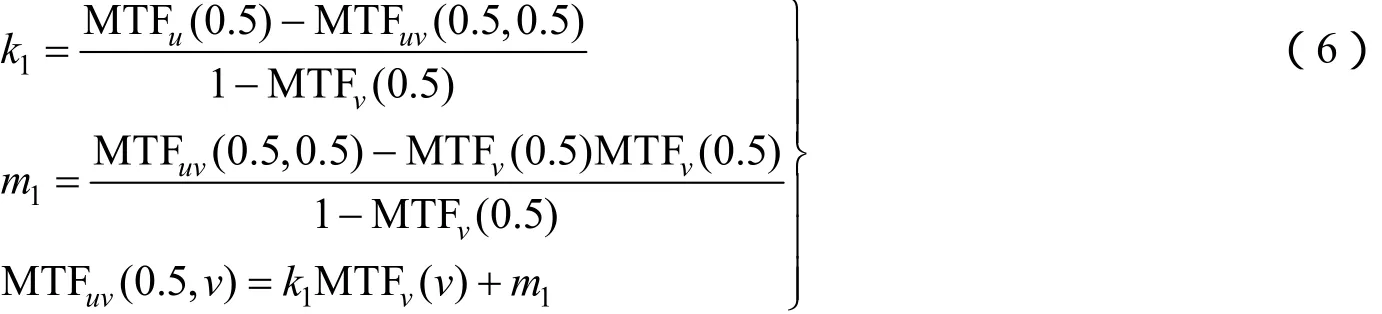
式中k1和m1为直线方程的斜率和截距；MTFuv(0.5,v)即为通过插值得到的MTF曲面v方向的一维边界函数。

3）通过一维插值获得第I象限中MTF曲面在(u,v)点的值MTFuv(u,v)为

式中k(v)，m(v)为与v相关的中间变量。

使用这种方法需要已知45°方向的一维MTF曲线，增加了构造难度；并且仅使用了45°方向的MTF曲线在u=0.5处的值，没有充分使用45°方向的完整MTF数据。在使用经验公式情况下，边界条件的准确度难以保证。

1.3 旋转插补方法

针对上述两种方法存在的不足，本文提出了一种新方法——旋转插补方法。基于旋转插补方法的两维MTF曲面的构建式为

式中θ为归一化角度，θ∈[0,1]；u,v∈ (0,0.5]；d为(u,v)点到原点距离。计算结果对应第I象限，利用曲面关于原点对称的特性，可得到其他各象限的结果。

以吉林大学2017年度本科教学改革研究项目为依托，研究将PBL教学法应用于.NET企业级应用开发系列课程教学，前期实践取得了较好效果。本文对PBL教学法运用于《企业级项目开发实训》课程实践教学的具体方法进行了总结与思考，以期通过对实践教学的以问题为导向的教学改革达到更好的教学效果。PBL教学法能激发学生的学习兴趣，提升学习主动性，为软件技术专业以能力为本位的教育思想提供了一条值得推广的有效途径，对计算机相关专业实践教学及课程教学都有巨大的应用价值。

在构造MTF曲面时，如能获得额外方向(φ,φ＜π/2)的一维MTF曲线作为边界条件，则可将旋转插补区间进行分段：将[0,π/2]区间分为[0,φ]和(φ,π/2]两个区间进行构造，这样就能减少MTF曲面重建的误差。

2 实验与分析

2.1 二维M TF曲面的模拟标准设计

由于不同系统的二维MTF曲面形状也各不相同，而且很难测量得到准确的MTF曲面。为定量研究不同方法构造二维MTF曲面的误差，本文设计了两种满足二维MTF曲面特性的函数：准高斯函数和4次多项式函数作为参考标准，用于模拟MTF曲面。设定各向不同性的约束条件：MTFu(0.5)=0.3、MTFv(0.5)=0.2和MTFu(0.5)=0.4、MTFv(0.5)=0.3。所有实验均在MATLAB 7.0环境[11]下进行。

（1）准高斯函数曲面

对于标准高斯曲面的表达式，当使用参数ρ＜0模拟（不满足独立性的）二维MTF曲面时，所构造的函数曲面在(u,v)=0的边界处会出现与常规MTF曲面不一致的局部极小现象。为此对式（2）的相关系数项做修改，得到“准高斯曲面”函数为

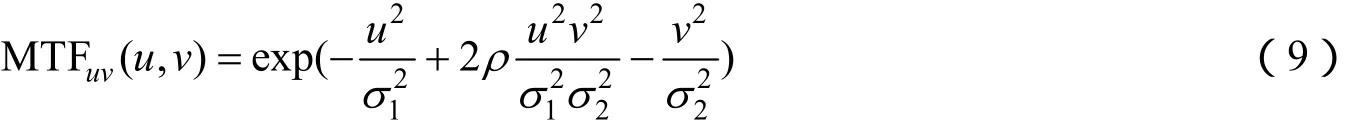
由约束条件可计算得到准高斯曲面的参数为：σ1=0.455 68，σ2=0.394 12；ρ为相关系数，可调整曲面的4个顶点值。取ρ=–0.15时，函数曲面如图2所示，其外形与取相同参数σ1和σ2且ρ=0的标准高斯曲面相似，但4个边界点的值大于标准高斯函数。

（2）4次多项式函数曲面

4次多项式函数曲面的数学表达式为

式中a，b为多项式系数。

由约束条件可计算得到参数：a=–1.809 1，b=–2.211 1，函数图形如图3所示。

2.2 实验设计

具体实验步骤如下：

1）用式（1）、（9）和（10）定义的（准）高斯函数以及4次多项式函数作为二维MTF曲面的模拟标准，记为MTFuv0(u,v)；

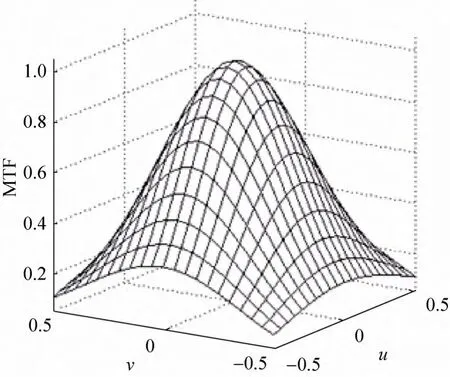
图2 二维准高斯曲面（ρ=–0.15）Fig.2 2-D QuasiGaussian surface（ρ= –0.15）

图3 4次多项式曲面（a=–1.809 1，b=–2.211 1）Fig.3 4-degree polynom ial surface（a= –1.809 1，b= –2.211 1）

2）根据U和V方向上精确的一维MTF函数曲线，分别用乘积法、插值法和旋转插补法构造MTF曲面：MTFuvi(u,v)；

3）计算MTFuvi(u,v)与标准二维MTF曲面的误差为

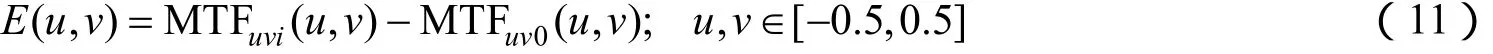
E(u,v)为构造曲面与标准MTF模拟曲面在(u,v)点的误差，以4次多项式函数作为标准的MTF曲面，构造误差分布见图4。

Eave为平均误差，与误差的大小和分布有关，期望值为0。

Rmse为均方差，表示构造曲面与标准MTF模拟曲面的总体偏差。实验结果见表1。

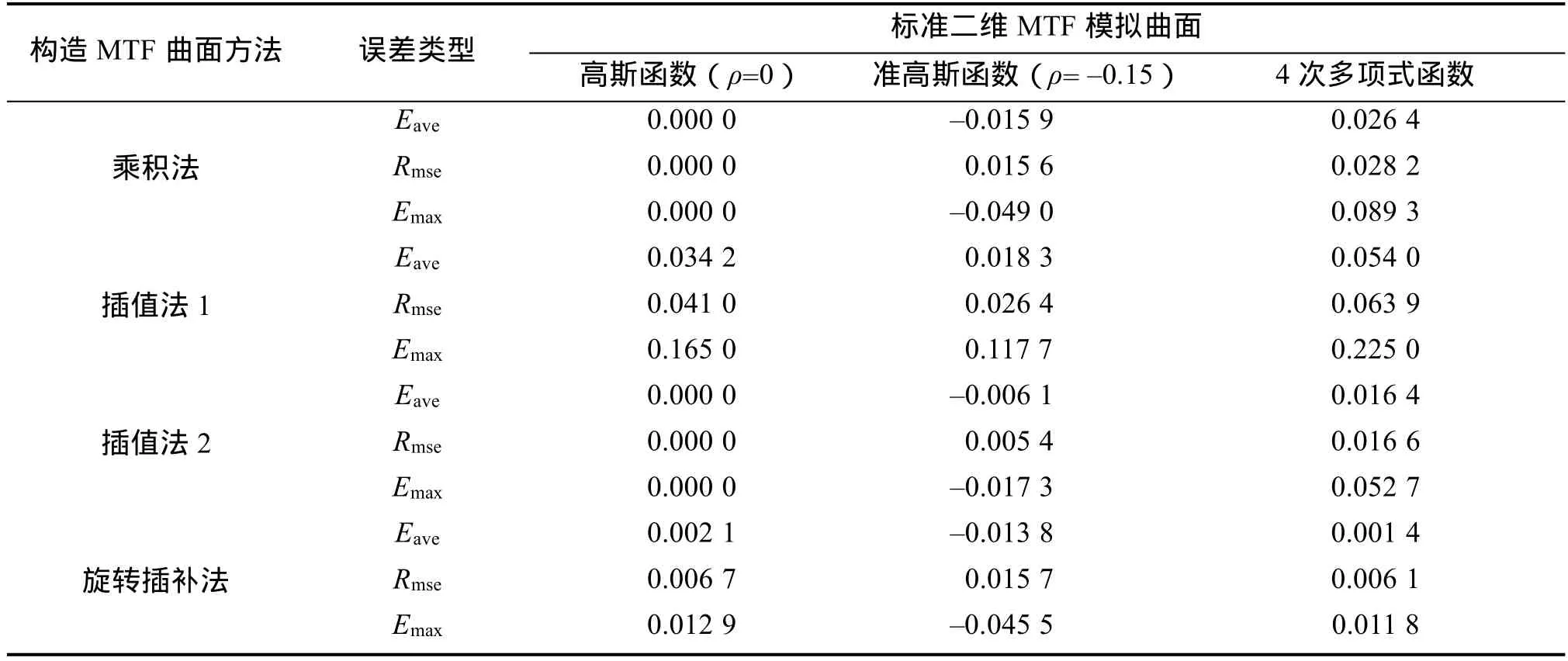
表1 M TF曲面构造误差Tab.1 The errors of MTF surface construction

表1中的Emax为实际最大误差。插值法1为式（4）估算4个边界点得到的计算结果，插值法2为由式（3）获取4个精确边界点得到的计算结果。

图4 MTF曲面构造误差分布图Fig.4 The errorsmaps of MTF surface construction

2.3 结果分析

由于高斯曲面（ρ=0）满足独立条件，作为模拟MTF曲面标准时，乘积法可通过U和V两个方向的一维高斯曲线构造得到精确的高斯曲面，所以表1中对应的3个误差都为0。

插值法的误差与4个边界点（MTF45°(0.5)）的精确度相关。在边界点为精确值时（见表1中插值法2），用准高斯函数（ρ=0，–0.15）作为标准，具有很好的重构性，其误差基本为0。在4次多项式函数作为标准曲面时，边界点的精确值为2.6×10–5；而由式（4）计算的估值为(0.2+0.3)/2×0.9=0.225，而导致重构误差增大：Emax=0.225，Rmse=0.0639。

相比之下，旋转插补法具有较小的重建误差，特别是在4次多项式函数作为标准时。但该方法需要对U、V两个方向的一维MTF曲线进行外推计算，因此对一维MTF曲线的精确性有一定的要求。

3 结束语

通过U、V两个方向的一维MTF曲线构造二维MTF函数曲面问题，实际上是一个由特定边界条件构建二维MTF函数曲面的数学问题[13]。为研究构建曲面模型算法，客观评价算法的有效性，在对现有的乘积法、插值法构造MTF函数曲面的方法进行了分析和研究，并提出了一种新的旋转插补法。最后设计使用了（准）高斯函数和4次多项式函数作为二维MTF曲面的模拟标准，对现有的各种方法的有效性进行了定量分析。其结果显示：各种方法在针特定的目标函数和条件时，有各自的优点；但总体上看，旋转插补法具有更好的适用性。

References)

[1] 张冬英,易维宁,王先华,等.空基遥感图像的MTF试验研究[J].安徽大学学报,2007,31(6):55-58.ZHANG Dongying,YIWeining,WANG Xianhua,etal.Experimental Study on MTF of Remote Sensing Image[J].Journal of AnhuiUniversity Natural Science Edition,2007,31(6):55-58.(in Chinese)

[2] 周春平,宫辉力,李小娟,等.遥感图像MTF复原国内研究现状[J].航天返回与遥感,2009,30(1):27-32.ZHOU Chunping,GONG Huili,LIXiaojuan,etal.The Summary ofMTFRestoration on Remote Sensing Image[J].Spacecraft Recovery&Remote Sensing,2009,30(1):27-32.(in Chinese)

[3] 顾行发,李小英,闵祥军,等.CBERS-02卫星CCD相机MTF在轨测量及图像MTF补偿[J].中国科学E辑信息科学,2005,35(Z1):26-40.GU Xingfa,LIXiaoying,M IN Xiangjun,etal:In-flightMTFMeasurementand MTFC of CBERS-02 Satellite CCD Images[J].Science in China Ser.E Information Sciences,2005,35(Z1):26-40.(in Chinese)

[4] 孙业超,朱晓波,郝雪涛.基于统一设备架构的影像实时MTF补偿方法[J].航天返回与遥感,2013,34(4):93-99.SUN Yechao,ZHU Xiaobo,HAO Xuetao.Optical Image Real-time MTF Compensation Method Based on CUDA[J].SpacecraftRecovery&Remote Sensing,2013,34(4):93-99.(in Chinese)

[5] 陈强,戴奇燕,夏德深.基于MTF理论的遥感图像复原[J].中国图象图形学报,2006,11(9):1299-1305.CHEN Qiang,DAIQiyan,XIA Deshen.Restoration of Remote Sensing Images Based on MTF Theory[J].Journal of Image and Graphics,2006,11(9):1299-1305.(in Chinese)

[6] 曾湧,于晋,陈世平.基于调制传递函数的航天遥感图像恢复研究[J].航天返回与遥感,2008,29(2):11-17.ZENG Yong,YU Jin,CHEN Shiping.Research on Remote Images Restoration Based on MTF[J].Spacecraft Recovery&Remote Sensing,2008,29(2):11-17.(in Chinese)

[7] 姚大杰.MTF测量方法研究[D].合肥:合肥工业大学,2012.YAO Dajie.MTFMeasurementTechnology Research[D].Hefei:HefeiUniversity,2012.(in Chinese)

[8] Borner A.Simulating Opto-electronic System for Remote Sensing w ith Sensor[C].Proc.SPIE 4881,Sensors,Systems,and Next-Generation Satellites.

[9] ElberG.Curve Evaluation and Interrogation on Surfaces[J].GraphicalModels,2001,63(3):197-210.

[10] Taeyoung Choi.IKONOS Satellite on Orbit Modulation Transfer Function(MTF)Measurement using Edge and Pulse Method-2001 report[R].A Thesis Subm itted in Partial Fulfillment of the Requirements for the Master of Science Major in Engineering South Dakota State University,2002.

[11] 赵海滨.MATLAB应用大全[M].北京:清华大学出版社,2012.ZHAO Haibin.TheMATLABApplication[M].Beijing:Tsinghua University press,2012.(in Chinese)

[12] 岳天祥,杜正平,刘纪远.高精度曲面建模与误差分析[J].自然科学进展,2004,14(3):300-306.YUE Tianxiang,DU Zhengping,LIU Jiyuan.Modeling and Error Analysis of High Accuracy Surface[J].Progress in Natural Science,2004,14(3):300-306.(in Chinese)

[13] 顾步云,周来水,刘胜兰,等.逆向工程中二次曲面拟合方法的研究[J].机械制造与自动化,2004,33(1):11-13.GU Buyun,ZHOU Laishui,LIU Shenglan,et al.Study on Algorithm of Quadric Surface Fitting in Reverse Engineering[J].Machine Building&Automation,2004,33(1):11-13.(in Chinese)

[14] 费业泰.误差理论与数据处理[M].北京:机械工业出版社,2005.FEIYetai.Error Theory and Data Processing[M].Beijing:Machinery Industry Press,2005.(in Chinese)