基于GPU的高光谱遥感主成分分析并行优化

柳家福 李欢 贺金平 刘天石 王启聪 吴泽彬,4

（1 南京理工大学计算机科学与工程学院，南京 210094）（2 北京空间机电研究所，北京 100094）（3 北京航空航天大学电子信息工程学院，北京 100191）（4 南京理工大学连云港研究院，连云港 222006）

0 引言

高光谱遥感具有较高的光谱分辨率，能够获取丰富的地表信息，是继多光谱遥感技术之后的一种新型遥感技术。其光谱分辨率小于10nm，波长范围在0.37～2.48μm之间，能从紫外线、可见光、近红外和短波红外等光谱区域获取大量且光谱连续的遥感数据。一幅高光谱图像通常包含了同一个地表区域内上百个不同波段的光谱信息[1]，如我国首次自主研制的搭载在HJ-1A星上的干涉型高光谱成像仪（HSI），能够以 115个波段同时对地表物质成像[2]。但丰富的遥感数据信息，在实际应用中提高了高光谱遥感数据传输和处理效率的难度。主成分分析（principal component analysis, PCA）是光谱特征提取常用的线性组合方法[3-4]，能够有效提取出特征光谱，降低光谱图像的数据量级，但是在实际的工程应用中存在降维计算速度慢的问题，尤其在处理海量的高光谱数据时十分耗时，严重影响高光谱图像处理的实时性，计算效率已成为其应用推广的瓶颈。如何快速降低高光谱图像的维数，提取出特征数据，是高光谱遥感图像处理面临的重要问题。

随着图形处理技术不断发展，尤其是NVIDIA公司使用类C语言开发的用于通用计算的CUDA框架问世之后[5]，具备CUDA框架的显卡可以支持大量的线程并行，而且能够动态的调度和执行。该框架中的单指令多线程执行模型，是对单指令多数据的一种改进，这种模型能够将执行数据的宽度作为硬件细节被隐藏起来，使硬件可以自适应不同的执行宽度，提高编程的灵活性。此外，图形处理器（graphic processing unit，GPU）的设计者将更多的晶体管作为执行单元，而不是像中央处理器（central processing unit，CPU）那样用作复杂的控制单元和高速缓存，因而在密集型的数据计算中GPU具有明显的优势，CPU则更擅长逻辑控制较多的数据运算。以上特点，使图像处理单元具有高度的并行计算和并行数据处理能力，成为能够辅助CPU计算的通用计算单元。有学者尝试利用GPU来提高PCA算法的执行效率，并取得了一定的成果。文献[6]比较了基于SSE与GPU两种方法对PCA算法的加速效果，结果证明基于GPU的PCA加速算法的最高加速比达到20倍，明显优于基于SSE（stream ing SIMD extensions）的加速算法，但效率仍有较大提高；文献[7]研究了光谱解混的GPU加速流程，其中PCA算法加速比最高可达122倍，但在特征分解部分采用乘幂法，该方法主要用于求取实矩阵的主特征值，求矩阵的全部特征值需要对矩阵进行降阶，而每降阶一次计算精度就会损失或降低一些，因此这种PCA算法的计算精度也较低。由于PCA算法的复杂性，部分计算过程并不适合GPU并行执行，因而如何设计适当的并行算法流程，在保证PCA并行算法的精度基础上提高计算效率，已成为快速遥感处理领域中亟待解决的问题。

针对PCA串行计算方法效率低、GPU并行算法精度难以保证的特点，本文提出基于GPU+CPU异构系统的PCA并行优化算法，将适合GPU加速计算的协方差矩阵计算与矩阵投影运算部分在GPU上执行，而特征分解部分采用改进的Jacobi单侧旋转算法在CPU上进行计算[8]，充分利用CPU与GPU各自的计算特性，在保证了PCA算法的精度的同时提高了该算法的计算效率。

1 基于PCA方法的高光谱遥感数据特征提取原理

高光谱遥感数据特征提取是将光谱数据特征按一定准则由原高维空间变换到较低维数空间，提取的特征应尽可能保留针对地物光谱差异的有价值信息[9]。一般通过对原始n维特征空间进行空间变换，然后求得其特征子空间。特征提取需要找到一个映射关系Q:X→Y，将原始特征空间的n个特征X=(X,X,X,…,X)T映射到维数较低的特征子空间Y中，使其通过这种映射关系产生m个新特征

1 2 3n

Y= (Y,Y,Y,…,Y)T，其中m＜n。

1 2 3m

PCA又称为 K-L变换，是高光谱特征提取常用的线性组合方法[1]。若X=(X1,X2,X3,…,Xn)T是n维随机变量，且均值E(X)=μ，协方差D(X)=Δ，考虑其线性变换:

可得:

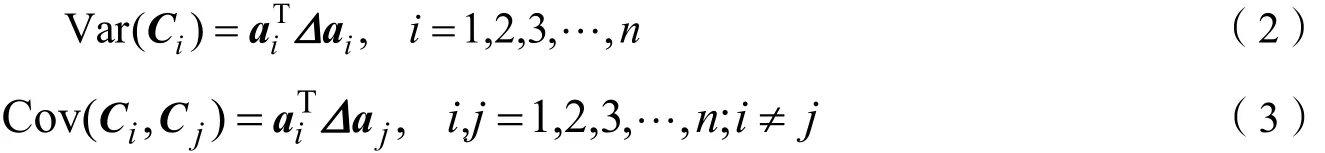
式中ai（i= 1,2,3,…,n）为X变换的系数矩阵；Ci（i= 1,2,3,…,n）为变换矩阵；Var(Ci)为Ci的方差；Cov(Ci,Cj)为Ci、Cj的协方差。

假设C1=a1TX为所求的第一主成分，则C1应能尽可能多地反映原有n个变量的信息，其信息可以用C1的方差来表达。该问题转化为求a1= [a11,a21,…,an1]T，使得在约束条件a1=1下，Var(Ci)达到最大值。可用拉格朗日乘数法求解，令

得到:

式中λ为拉格朗日乘子；为对φ关于自变量a1求导；为对φ关于自变量λ求导；I为单位矩阵。由于a1≠0，因此∑-λI=0，即转化为求解协方差矩阵Σ特征向量和特征值问题。假设λ=λ1是∑的最大特征值，则相应的单位特征向量a1即为所求值。以此类推，求X的第i个主成分需要先求出协方差矩阵∑的第i个特征值λi对应的单位特征向量ai，为了更有效地表征原来变量的信息，前i-1个主成分体现的信息不希望在Ci中出现，则需添加约束条件j= 1,2,3,…,i-1；通过i= 1,2,3,…,n进行运算，即可得到变换后的矩阵。传统的PCA算法流程如图1所示。

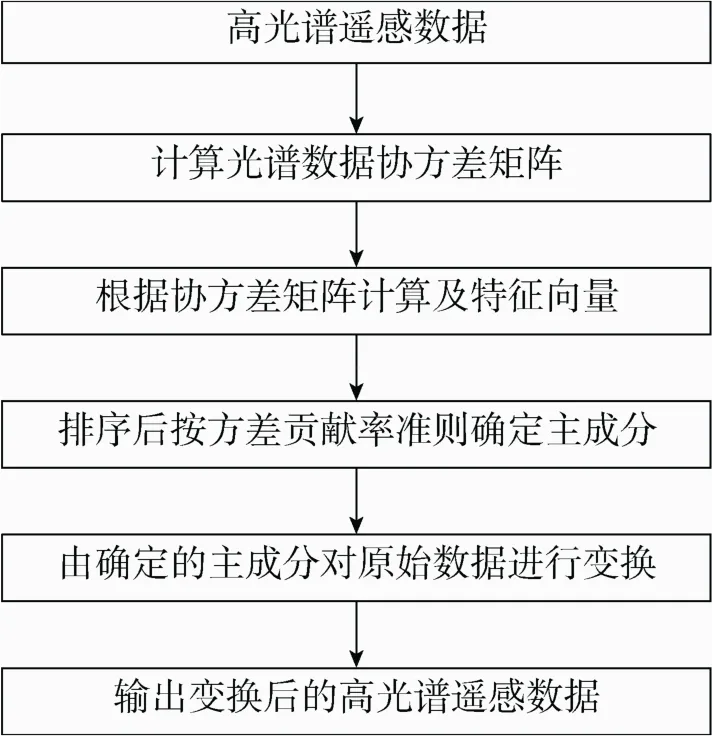
图1 传统PCA算法流程Fig. 1 Traditional PCA algorithm flow

计算时通常只需要选择与最大的m个特征值相对应的特征向量即可，这样便可以减少原始矩阵的维数，还保留了主要的数据信息。

2 基于GPU+CPU异构系统的主成份分析方法并行优化

2.1 PCA并行优化设计

根据上述分析，PCA算法的关键步骤在于协方差矩阵的计算、特征分解以及光谱数据投影。其中协方差矩阵计算最为耗时，是PCA算法并行优化的重点[10-11]；特征分解则是该算法的性能瓶颈，对精度有很大影响；光谱矩阵投影是常规的矩阵运算，十分适合GPU并行加速。

高光谱遥感数据的协方差矩阵计算，用传统方法需要对各波段图像求均值并对所有像元逐一去中心化，但由于原始高光谱矩阵的数据量大，该方法的执行效率较低。本文对其进行改进，如式（6）所示，若)是高光谱图像任意两个波段对应的像元向量，∑ij为其协方差，s为高光谱图像像元个数。使用传统方法需要对N i、N j中每个像元分别求均值，由于s的量级通常大于 105，因而计算量很大。改进后的方法只需对结果去一次均值即可，即先求N i、N j对应像元乘积的累加和，再求出N i、N j对应的均值，二者相减即可求出波段i和j的协方差∑ij，从而极大地提高运行效率。

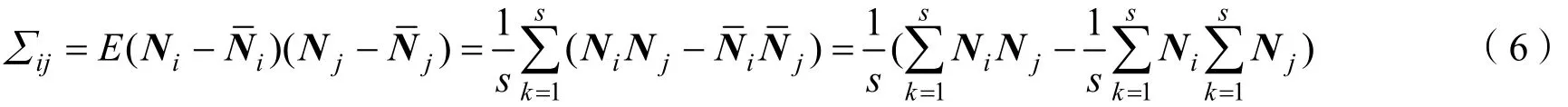
对于协方差矩阵的特征分解，求解算法很多，如 QR算法[12]、乘幂法[7]、MRRR算法[13]、Arnoldi算法[14]、Jacobi-Davidson[15]算法等，但这些算法都有各自的特性，或是通用算法，收敛速度慢；或是精度不高，准确性低。如文献[7]中提出的PCA并行优化算法（以下称为SPCA算法），利用乘幂法进行特征分解，该方法采用矩阵乘法运算，适合并行加速，但是由于乘幂法求矩阵的全部特征值需要对矩阵进行降阶运算，导致相邻特征对数据依赖较大，每降阶一次计算精度就会降低一些，所以降阶法实际上只可使用少数几次，仅适用于求矩阵前几个按模最大特征值及相应特征向量。本文采用了Jacobi单侧旋转算法求解协方差矩阵的特征分解值，该算法是对传统Jacobi双侧旋转算法的改进。Jacobi算法的主要思想是通过正交相似变换将一个实对称矩阵对角化，从而求出该矩阵的全部特征值和对应的特征向量。已知协方差矩阵Σ是对称方阵，设λ为其特征值，a为其特征向量矩阵，则:Σa=λa。由于∑=ΣT，所以ΣTΣa=Σλa=λλa，这说明λ2为ΣTΣ的特征值，a为ΣTΣ的特征向量，即ΣTΣ与Σ具有相同的特征向量a，且特征值具有平方关系。现使用Givens旋转变换对Σ进行一系列的列变换，得到方阵Q，使其各列两两正交，即ΣV=Q，这里V为正交化过程的变换方阵。由于QTQ为n阶对称方阵，因此可得即可得到特征值λ，其中V即为所求特征向量。由以上分析可知，Jacobi单侧旋转法仅需对对称方阵实施列变换，就可使数据相关关系仅在同列之间，不但计算速度快，而且精确性较高。

根据上述方法，将求得的特征向量矩阵a= [a1,a2,a3,…,am]T与光谱矩阵N进行矩阵运算，即可得到经过特征提取的降维矩阵。

本文设计的基于GPU+CPU异构系统的高光谱遥感主成分分析并行优化算法如图2所示，其中s为高光谱图像像元个数；M为高光谱图像及其自身转置乘积；M uv为第u、v波段对应像元向量内积；Su、Sv分别为第u、v波段对应像元向量累加和。当高光谱数据加载到内存后，CPU端将数据由主机端拷贝到GPU的Global Memory；由设备端执行Kernel函数，计算高光谱数据的矩阵乘积以及高光谱图像像元向量的累加和；再由改进的协方差矩阵公式计算出高光谱图像的协方差矩阵；由CPU端辅助计算出协方差矩阵的特征向量矩阵，并按特征值的大小进行排序；最后再由GPU计算出特征图像，并将结果拷回主机端内存。

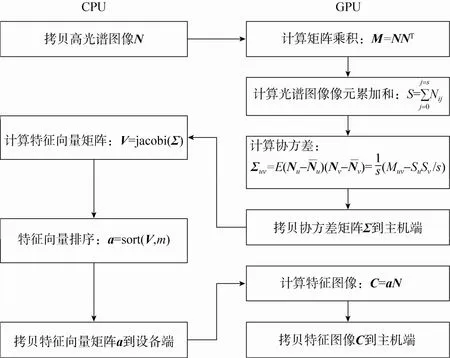
图2 PCA方法的并行优化算法流程Fig. 2 Parallel optim ization flow of PCA

2.2 协方差矩阵计算并行优化

计算高光谱数据的协方差矩阵Σ，需要对高光谱数据及其转置求矩阵乘积，该过程十分适合 GPU并行加速，可采用CUBLAS库中的矩阵乘积函数进行计算，此函数会发布与结果矩阵相同大小的线程个数来执行计算，效率较高。为了计算矩阵N的协方差，还需要知道每个波段图像的均值，由于各波段求和相互独立，可以使用GPU进行计算，而各波段内部求和可采用Reduction的方法来进行计算，为此需要发布一个名为SumKernel的核来执行该操作，其中SumKernel为核函数名称，本文实验中，该核创建与原始光谱图像波段数n相同个数的线程块，每个块内包含256个线程，计算一个波段图像累加和的线程，在一个块内，块内线程共享一个共享存储器，计算时使用合并访问将数据拷贝到该共享内存内可提高读取数据的速度。如图3所示，描述了该累加和的缩减过程。计算结束后，根据式（6），将光谱数据乘积减去该均值，即可求出光谱矩阵的协方差，该过程如图4所示。

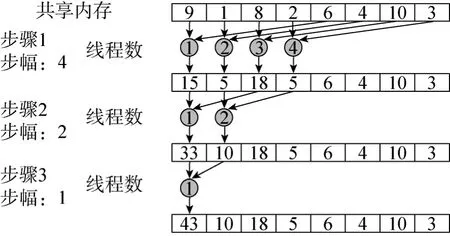
图3 GPU累加和归约过程Fig. 3 Reduction process of summation on GPU

图4 协方差矩阵计算并行优化流程Fig.4 Parallel optim ization flow of covariance matrix calculation

2.3 特征分解计算及矩阵投影并行优化

通过以上方法计算得到图像各波段的协方差矩阵Σ后，需要计算该矩阵的特征分解值，记特征向量为a= [a,a,a,…,a]T，由以上分析可知，乘幂法适合GPU并行加速，但每降阶一次，计算精度就会损

1 2 3m失或降低一些，实际中只可用少数几次。本文采用Jacobi单侧旋转算法进行求解，该算法是Jacobi双侧旋转法的改进，精确性较高，尽管数据之间的依赖性较大，不能在GPU上加速，但这已不是并行加速的瓶颈。得到特征向量矩阵后，按方差大小进行排序，取前m个特征向量a，将其与矩阵N相乘，即得到降维矩阵C。这一步仍然是标准的矩阵相乘运算，可以调用GPU中CUBLUAS库的内置函数cublasSgemm来执行。

与SPCA方法相比，本文提出的优化算法有两方面改进:1）在波段对应图像累加和计算方面，采用线程折半顺序累加，减少了bank冲突，提高了访存效率；2）在计算协方差矩阵特征对时，使用Jacobi单侧旋转法，不但精度较高，而且速度也接近SPCA方法中的乘幂法。

3 实验结果与分析

根据以上算法，本文采用NASA的AVIRIS高光谱图像数据（美国内华达州南部沙漠的Cuprite数据）进行模拟测试，图像已经经过大气校正并且已转换为光谱反射率，原有224个波段，去除1～3、105～115、150～170、223～224噪声段，剩余波段数为187；然后从中截取3个不同像元大小的图像（300×300像元、450×450像元、614×512像元）进行试验测试，其中614×512像元是在NASA网站上下载的原始高光谱图像。本文实验环境为:英特尔Xeon E5603四核CPU；主频为1.6GHz；内存为8 Gbyte。使用的GPU为Nvidia Quadro 600，拥有96个CUDA cores和1Gbyte的显存。软件环境为:Windows7 专业版64bit操作系统；Visual Studio 2010集成开发环境和CUDA 5.0版本工具包。

3种不同数据规模下，串行算法和并行算法的运行时间以及并行算法的加速比见表1。结果表明，随着数据规模的增大，加速效果更加明显，当数据大小为614×512像元时，最高加速比可达141倍，其并行算法优势明显。

表1 不同数据的执行时间及加速比Tab. 1 Execution time and speedup of different hyperspectral images

表2比较了本文方法（JPCA算法）、SPCA以及MATLAB计算特征分解中特征值结果，由表中的数据可知，采用本文的特征值求解算法，其特征值结果和 MATLAB软件计算的结果完全相同，而 SPCA方法尽管适合GPU并行优化，但其计算精度却有较大的误差。

表2 PCA特征值比较Tab. 2 Eigenvalues comparison of PCA

综合以上实验数据可以验证，本文提出的基于GPU+CPU异构系统的高光谱遥感PCA并行优化算法，在保证算法精度的同时，计算效率也得到了显著提高。

4 结束语

本文从高光谱遥感图像数据处理的实时性问题出发，提出了基于GPU+CPU异构系统对高光谱遥感图像进行特征提取的PCA并行优化方法，经实验验证，达到以下结果:

1）改进了协方差矩阵的计算步骤，优化了高光谱像元去均值的计算流程，减少了运算次数，避免了多次访存操作；

2）优化了GPU中的累加和计算，减少了非合并访问；

3）在特征分解部分，使用精确度更高的Jacobi单侧旋转算法进行求解，并将该部分设计在CPU端执行，不但提高其计算效率，而且精确度很高；

4）充分利用GPU的存储层次模型，将部分数据存储在共享内存，减少对全局内存的访问，节省了访存时间。

GPU的并行优势主要体现在密集型数据计算上，将迭代次数多、需要反复通信的特征分解放在CPU端执行，也体现了基GPU+CPU异构计算的模型思想。本文提出的PCA并行优化方法达到了高光谱数据实时特征提取的效果。但在实际应用过程中还需考虑GPU显存的限制，当高光谱遥感数据超出GPU的显存能力时，如何对数据进行分块处理，平衡数据块在存储设备间传输的时间开销，需要进一步的研究。

（References）

[1] 童庆禧, 张兵, 郑兰芳. 高光谱遥感—原理、技术与应用[M]. 北京: 高等教育出版社, 2006.TONG Qingxi, ZHANG Bing, ZHENG Lanfang. Hyperspectral Remote Sensing-Principles, Technology and Applications[M]. Beijing: Higher Education Press, 2006. (in Chinese)

[2] 王爱春, 闵祥军, 李杏朝, 等.“环境-1号”A星高光谱成像仪飞行定标[J]. 航天返回与遥感, 2009, 30(3): 34-41.WANG Aichun, M IN Xiangjun, LI Xingchao, et al. In-flight Absolute Calibration of the HJ-1A HSI[J]. Spacecraft Recovery& Remote Sensing, 2009, 30(3): 34-41. (in Chinese)

[3] Kambhatla N, Leen T K. Dimension Reduction by Local Principal Component Analysis[J]. Neural Computation, 1997, 9(7):1493-1516.

[4] Manolakis D G, Marden D B. Dimensionality Reduction of Hyperspectral Imaging Data Using Local Principal Components Transforms[C]//Defense and Security. International Society for Optics and Photonics, 2004: 393-401.

[5] Manavski S A, Valle G. CUDA Compatible GPU Cards as Efficient Hardware Accelerators for Smith-Waterman Sequence Alignment[J]. BMCbioinformatics, 2008, 9(2): 10-19.

[6] Joth R, Antikainen J, Havel J, et al. Real-time PCA Calculation for Spectral Imaging (Using SIMD and GP-GPU)[J]. Journal of Real-time Image Processing, 2012, 7(2): 95-103.

[7] Sánchez S, Ramalho R, Sousa L, et al. Real-time Implementation of Remotely Sensed Hyperspectral Image Unm ixing on GPUs[J]. Journal of Real-Time Image Processing, 2012: 1-15.

[8] 李平. 基于FPGA的矩阵特征值并行计算研究[D]. 重庆: 重庆大学, 2013: 44-47.LI Ping. Study on FPGA-based Parallel Computing of the Matrix Eigenvalues[D]. Chongqing: Chongqing University, 2013:44-47. (in Chinese)

[9] 何明一, 畅文娟, 梅少辉. 高光谱遥感数据特征挖掘技术研究进展[J]. 航天返回与遥感, 2013, 34(1): 1-12.HE M ingyi, CHANG Wenjuan, MEI Shaohui. Advance in Feature M ining from Hyperspectral Remote Sensing Data[J].Spacecraft Recovery & Remote Sensing, 2013, 34(1): 1-12. (in Chinese)

[10] LU J, ZHANG B, HUANG W, et al. IHS Transform Algorithm of Remote Sensing Image Data Fusion Based on GPU[J].Computer Engineering, 2009, 35(7): 261-263.

[11] SONG J, ZHOU S. Fast Image Matching Based on GPU Parallel Computing[J]. Journal of Hubei University for Nationalities:Natural Science Edition, 2011, 29(3): 306-310.

[12] 袁晖坪. 关于酉对称矩阵的QR分解及其算法[J]. 系统科学与数学, 2012, 32(2): 172-180.YUAN Huiping. On QR Factorization and Algorithm for Unitary Symmetric Matrix[J]. Journal of Systems Science and Mathematical Sciences, 2012, 32(2): 172-180. (in Chinese)

[13] Petschow M, Bientinesi P. The Algorithm of Multiple Relatively Robust Representations for Multi-core Processors[M].Berlin: Springer Berlin Heidelberg, 2012: 152-161.

[14] Guan L, Gao J L, Wang Z W, et al. A Refined Arnoldi Algorithm Based Krylov Subspace Technique for MEMS Model Order Reduction[J]. Key Engineering Materials, 2012, 503: 260-265.

[15] Andrzejew ski J. On Optimizing Jacobi–Davidson Method for Calculating Eigenvalues in Low Dimensional Structures Using Eight Band k/p Model[J]. Journal of Computational Physics, 2013, 249: 22-35.