α-蒎烯的发酵动力学模型

任 萌，高国富，咸 漠，杨建明，*

（1.南京农业大学生命科学学院，江苏南京 210095；2.中国科学院生物基材料重点实验室，中国科学院青岛生物能源与过程研究所，山东青岛 266101）

α-蒎烯的发酵动力学模型

任 萌1，2，高国富1，*，咸 漠2，杨建明2，*

（1.南京农业大学生命科学学院，江苏南京 210095；2.中国科学院生物基材料重点实验室，中国科学院青岛生物能源与过程研究所，山东青岛 266101）

以α-蒎烯生产菌株YJM28为供试菌株，对其发酵动力学特征进行了研究。通过对Logistic等方程进行了最优参数估计和非线性拟合，得出了α-蒎烯的发酵动力学模型及相关参数。并且对动力学模型的拟合曲线分析可知，发酵实验值与模型预测值能够较好的吻合，说明所建立的发酵动力学模型能够较好的反应α-蒎烯的发酵过程。

α-蒎烯，发酵动力学模型，拟合

α-蒎烯是一种重要的天然产物，主要存在于松节油当中，广泛应用于农药、香料、医药以及精细有机合成工业[1-2]。利用微生物法生产α-蒎烯具有原料来源广泛，生产不受季节限制，生产周期短以及易扩大生产等优点。由于遗传背景清楚，基因操作简单，大肠杆菌被广泛应用于微生物发酵领域中[3-4]，利用重组后的大肠杆菌进行α-蒎烯的生产研究报告较少，而有关其发酵过程中的生长特性、发酵动力学分析方面研究未见文献报道。

本文以重组大肠杆菌YJM28作为实验菌株，研究 了 该 菌 株 的 发 酵 动 力 学 性 质 。 利 用 Logistic 及Luedeking-Piret方程建立了该菌的菌体生长、产物合成以及底物消耗的动力学模型。通过Matlab 2012软件进行实验数据处理，拟合出所有的模型参数，建立发酵动力模型[6]。最后对模型预测值与实验真实值之间进行比较，验证所得模型的可靠性。本文目的是初步确定YJM28的发酵动力学模型，为进一步优化及放大提供理论依据。

1 材料与方法

1.1 材料与仪器

重组大肠杆菌YJM28（recombination Escherichia coli YJM28） 本实验室构建及保存；氨苄青霉素 北京索来宝公司；氯霉素 购自北京东胜泰博科技有限公司；诱导剂IPTG 购自合肥BIOSHARP公司；蛋白胨 天津大茂试剂有限公司；其余试剂 均为国药公司分析纯试剂。

种子培养基 蛋白胨10g，酵母粉5g，NaCl 10g，蒸馏水1000mL，121℃灭菌20min，冷却后使用；发酵培养基（1L） 柠檬酸铁铵0.15g，K2HPO4·3H2O 4.9g，C6H8O7·H2O 0.525g，蒸馏水1000mL，121℃灭菌20min，冷却后使用；葡萄糖（20g/L）、MgSO4（1mol/L） 115℃灭菌30min，冷却后4℃保存；氨苄青霉素（100mg/L）、氯 霉 素（34mg/L）、IPTG溶 液（20mg/mL） 过 滤 灭 菌后-20℃保存；微量元素溶液（0.37g（NH4）6Mo7O24·4H2O，0.29g ZnSO4·7H2O，2.47g H3BO4，0.25g CuSO4·5H2O，1.58g MnCl2·4H2O，用 蒸 馏 水 定 容 至 100mL）过 滤 灭菌后4℃保存。

Cary-50紫外-可见分光光度计 美国瓦里安技术有限公司；SP-6890气相色谱仪 山东鲁南瑞红化学分析仪器有限公司；IS-RDS3恒温振荡器 美国CRYSTAL公司；1-14台式高速离心机 美国Sigma公司；SBA-40C生物传感器 山东省微生物研究所。

1.2 实验方法

1.2.1 种子培养 用无菌牙签挑取单克隆于3mL LB培养液中活化，再以5%接种量接入40mL LB液体培养基中，37℃，180r/min培养4h后准备转接。

1.2.2 发酵培养 按1%接种量转接上一步活化好的种子至590mL厌氧培养瓶中，37℃，180r/min培养至OD600达到0.6～0.9，接着，以终浓度为0.04mmol/L的IPTG诱导，诱导后加瓶塞并将培养温度调至30℃，转速不变，连续发酵48h[5]。

1.2.3 α-蒎烯发酵液的检测 发酵液在10000r/min下离心1min，取上清液稀释，采用SBA-40C生物传感器分析仪分析葡萄糖浓度；细胞密度用紫外-可见风光光度计测定OD600，1个OD600菌体密度相当于0.2g/L菌体干重；发酵产物采用SP-6890气相色谱仪进行检测（柱型号HP-INNOWAX；检测器FID，200℃；进样量1mL摇瓶上空气体；柱温升温程序50℃保温0.5min，然后4℃/min升温至70℃，再以20℃/min升温至250℃，保温10min；气化室200℃；Rt≈3.75min）。

1.2.4 数 据 处 理 所 得 实 验 结 果 在 Logistic 以 及Luedeking-Piret方 程 基 础 上 ，建 立 α - 蒎 烯 产 生 菌YJM28发酵过程中菌体生长、产物形成、底物消耗的动力学模型[6]。应用Matlab 8.0软件处理实验数据，拟合模型及其相关参数，建立发酵动力学模型。

2 结果与讨论

2.1 α-蒎烯发酵过程代谢变化特征

图1 YJM28生产α-蒎烯发酵过程曲线Fig.1 Fermentation curve of YJM for fermentation α-pinene

YJM28生产α-蒎烯整个发酵过程代谢变化如图1所示。从图1中可以看出，菌体的生长曲线呈现出典型的S型曲线，供试菌株的延滞期较短，菌体生长较为迅速，0～4h为菌株的延迟期，菌体生长较为缓慢，4～16h为对数生长期，菌体生长迅速，20h达到稳定期，菌体生长趋于稳定，菌浓增加变小，在发酵24h时菌体干重达到0.43g；发酵产物α-蒎烯浓度变化过程与细胞生物量变化趋势稍有不同，α-蒎烯浓度在20h达到最大，产物浓度达到32.8mg/L，此后稍有下降，但是较为缓慢，仍可在较高水平维持一段时间。从菌株生长和产物合成曲线可以看出，细胞生长伴随着产物的合成，待菌体生长达到稳定后，产物合成也趋于稳定。因此可以推测YJM28菌株生产α-蒎烯的发酵类型为生长部分偶联。从限制性底物消耗曲线可知葡萄糖利用与细胞生长基本成对称关系[7]。

2.2 动力学模型的建立

发酵动力学模型一般由3部分组成：菌体生长动力学模型、产物形成动力学模型、底物消耗动力学模型。按照建模方法来分，可以将动力学模型分为三类：结构模型、半经验模型以及经验模型。目前，国内学者所构建的多属于经验或者半经验模型。其中，半经验模型建模方式较为简单，易于分析，故此应用范围较广。建模目的是为了实现发酵过程控制的最优化[8]。

2.2.1 菌体生长动力学模型 描述微生物生长动力学的模型很多，以Monod方程和Logistic方程最为简单常用[7]。前者是一种近乎理想的模型，它不考虑菌体浓度的增加对菌体生长的抑制作用，主要用来描述非抑制性单一底物限制下的细胞生长。后者作为典型的S型曲线，能够较好地反应发酵过程中因菌体浓度增加对自身生长造成的影响，能够较好地拟合发酵过程中的菌体生长规律。Logistic方程形式如下：

其中：μmax是最大生长速率（h-1）；X表示菌体干重（g/L）；t是发酵时间（h）。在发酵初始，当t=0时，此时菌浓X远小于Xm，因此X/Xm项可以忽略不计，方程表示菌体呈指数形式生长；当处于稳定期，X=Xm，方程表示菌体停止生长。对式1进行积分，可得

式（1）是YJM28菌体发酵过程中的菌体生长动力学模型表达方程，式（2）是其积分形式。

2.2.2 产物形成动力学模型 由于发酵产物形成复杂，Gaden[9]将产物形成与细胞生长之间的关系分为3类：I类发酵，产物形成于细胞生长相偶联；II类发酵，产物形成与细胞生长部分偶联；III类发酵，产物形成与细胞生长不偶联。为此，Luedeking和Piret[10]总结了下述公式来描述产物形成与细胞生长的关系：

其中，α表示与菌体生长相关的产物生成系数，β表示与菌体量相关的产物生成系数。当α≠0，β=0时表示产物形成与生长偶联；当α，β≠0时，产物与生长部分偶联；α=0，β≠0时，产物与生长不偶联。根据图1可以看出，YJM28应该属于II类发酵，是菌体生长与产物合成部分偶联，可以用Luedeking-Piret方程表示[11]。联合式（1），（2），（3）并积分得到如下公式：

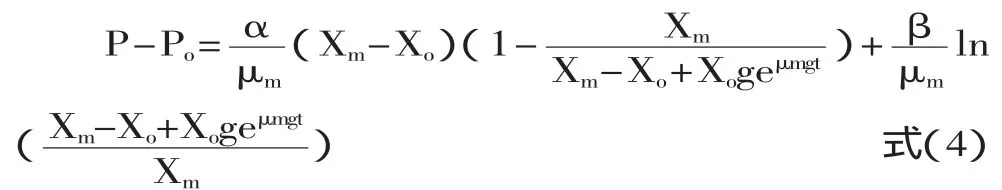
其中，P：产物α-蒎烯浓度（mg/L）；Po：产物的初始浓度（mg/L）；α：生长偶联系数（mg·L-1）；β：生长偶联系数（L·mg-1）。

当Po=0，Xo对产物的影响忽略不计，式4可简化为：

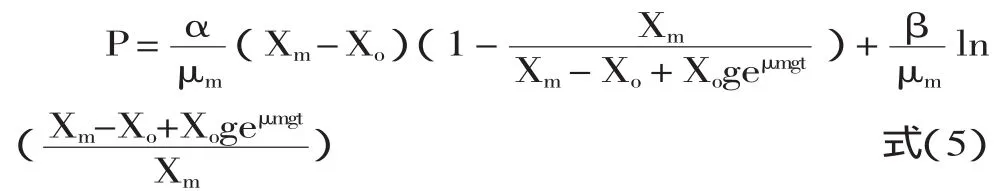
2.2.3 底物消耗动力学模型 根据物料守恒原理，限制性底物消耗主要用于三部分，即：菌体的生长、产物的合成以及维持细胞自身的代谢。由于α-蒎烯发酵过程中只有底物葡萄糖作为主要能量来源在随着发酵时间延长被不断消耗，因此，选择建立在单一限制性底物基础上的底物消耗动力学方程进行底物消耗动力学模型的建立，该方程可用Luedeking-Piret-Like方程[9]定量表示：

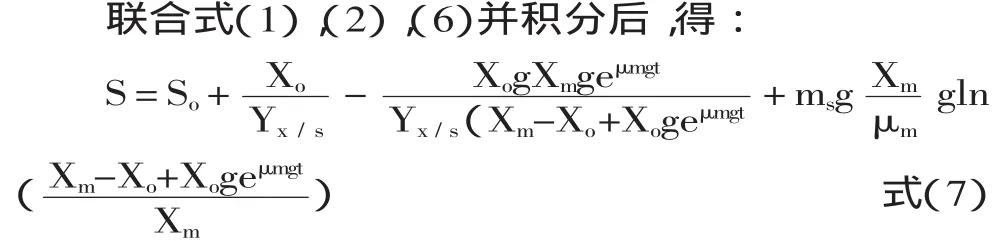
2.3 模型参数求解

采用麦夸特算法，以误差平方和最小为目标，通过Matlab软件中cftool工具箱进行非线性拟合，获得参数值[12]。根据发酵结果获得模型参数的初步估计值，不断拟合，直至得到全局收敛的最优化参数估计[13]。结果见表1。

根据表1结果，可得α-蒎烯发酵动力学模型为：

菌体生长动力学模型：

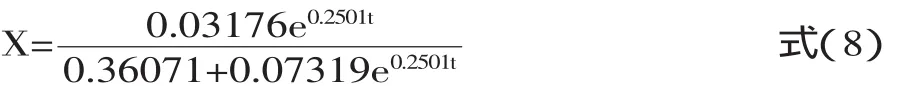
产物合成动力学模型：

底物消耗动力学模型：

2.4 拟合曲线分析

为进一步分析模型可靠性，运用软件得到的α-蒎烯发酵过程拟合曲线如图2～图4所示。图中实线代表模型预测值，虚线则表示实验测试值。

由图2～图4可以看出，曲线拟合结果较为理想，并且从菌体生长、产物合成、底物消耗的实验测试值与模型预测值随时间变化曲线上看，两者比较接近，经过计算，误差都在5%之内，表明动力学模型选择正确，模型拟合良好，能够真实的反映α-蒎烯的发酵过程。

图2 α-蒎烯分批发酵细胞生长实验值与模型计算值的比较Fig.2 Comparison of the predicted data with experimental data on biomass growth

图3 产物形成模型计算值与实验值比较Fig.3 Comparison of the predicted data with experimental data on alpha-pinene yield

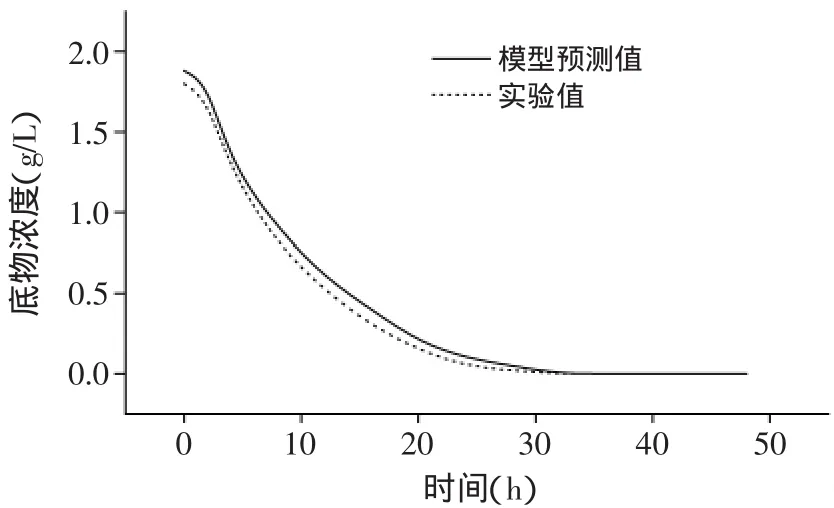
图4 底物消耗模型计算值与实验值比较Fig.4 Comparison of the predicted data with experimental data on substrate consumption

表1 发酵动力学模型估计值Table 1 Estimated values of kinetics model of fermentation

3 结论与讨论

由于微生物发酵整个过程包含有许多因素，例如生长、繁殖、维持、死亡、溶胞等，因此工程上的理论在应用之前要进行合理的简化，也就是说需要采用特定的模型来描述[14]。在分批发酵过程当中，一般采用均衡生长的非结构模型，即菌体细胞随着生长时间的延长，胞内各组分以相同比例增加，不考虑外界环境对菌体组成的影响[15]。本实验建立的各种模型就是基于以上假设而定。

本实验对重组大肠杆菌YJM28的菌体生长、α-蒎烯合成以及基质消耗的动力学进行了研究。结果表明，构建的模型基本真实的反映了菌体发酵的过程变化，尤其是菌体生长的模型拟合较好。在发酵前期，产物合成以及底物消耗的模拟值与实验值有较小的偏差。推测可能是实验条件所限，由于产物是气体形式存在于厌氧摇瓶发酵尾气当中，发酵过程中不追加葡萄糖，初始葡萄糖浓度较低以保持菌体在生长的初期生长速率不能过快，造成后期在诱导阶段菌体产物合成能力下降[16]。因此，在描述α-蒎烯产生时不能单纯的只考虑细胞生物量，还必须考虑以上诸因素的影响，才能不断的修正所建立的动力学模型使之能更真实的描述发酵过程。

利用麦夸特算法，以误差平方最小为目标，通过Matlab软件中cftool工具箱进行非线性拟合，可以获得待解参数。根据发酵结果获得模型参数的初步估计值，经过不断拟合直至得到全局收敛的最优化参数估计，通过非线性拟合求解得到参数数值。而且从菌体生长、产物合成以及底物消耗与时间关系曲线上看，动力学模型选择正确，拟合效果良好，较真实的反映了α-蒎烯的发酵全过程。

[1]李凝. 蒎烯 化学性 质的 应 用[J]. 广 西化 工，2000，29（1）：37-38.

[2]Meylemans H A ，R L Quintana， B G Harvey.Efficient conversion of pure and mixed terpene feedstocks to high density fuels[J].Fuel，2012，97：560-568.

[3]Jian-ming Yang，Mo Xian，Si-zheng Su，et al.Enhancing production of bio-isoprene using hybrid MVA pathway and isoprene synthase in E.coli[J].Plos One，2012，7（4）：1-7.

[4]Jiang M ， Chen X ， Liang L et al.Co-expression of phosphoenolpyruvate carboxykinase acid and nicotinic phosphoribosytransferase for succinate production in engineered Escherichia coli[J].Enzyme Microb Technol，2014，56：8-14.

[5]Jian-ming Yang，Qing-juan Nie，Meng Ren，et al.Metabolic engineering of Escherichia coli for the biosynthesis of alphapinene[J].Biotechnol for Biofuels，2013，6：60.

[6]臧春荣，夏凤毅. 微生物动力学模型[M]. 北京：化学工业出版社，2003.

[7]Bouvile M.Fermentation kinetics including product and substrate inhibitors plus biomass death：A mathematical analysis [J].Biotecnol Lett，2007，29：737-741.

[8]田雪，解鑫，周晓杭，等.地衣芽孢杆菌产β-甘露聚糖酶分批发酵动力学模型[J]. 中国农学通报，2013，29（18）：193-199.

[9]Elmer L Gaden J.Fermentation Process Kinetics[J].Journal of Biochemical and Microbiological Technology and Engineering，1959，1（4）：413-429.

[10]Robert Luedeking，Edgar L Piret.A Kinetic study of the lactic acid fermentation batch process at controlled pH[J]. Journal of Biochemical and Microbiological Technology and Engineering，1959，1（4）：393-431.

[11]Colombie S，Malherb S，Sablayrolles J M.Modeling alcoholic fermentation in enological conditions：Feasibility and interest[J]. Am J Enol Vitic，2005，56：238-245.

[12]Jessica L Linville，Miguel Rodriguez Jr，Jonathan R Mielenz et al.Kinetic modeling of batch fermentation for populus hydrolysate tolerant mutant and wild type strains of Clostridium thermocellum[J].Bioresource Technology，2013，147：605-613.

[13]João Moreira Neto，Daniella dos Reis Garcia，Sandra Marcela Go’mez Rueda，et al.Study of kinetic parameters in a mechanistic model for enzymatic hydrolysis of sugarcane bagasse subjected to different pretreatments[J].Bioprocess Biosyst Eng，2013，36：1579-1590.

[14]程新，夏海林，黄林，等.红曲霉JR发酵动力学模型的建立[J]. 江西农业大学学报，2010，32（3）：590-594.

[15]Ma L， Li C， Yang Z et al.Kinetic studies on batch cultivation of Trichoderma reesei and application to enhance cellulase production by fed-batch fermentation[J].J Biotechnol，2013，166（4）：192-197.

[16]Mitchell D A，Meien O F，Krieger N，et al.A review of recent developments in modeling of microbial growth kinetics and in traparticle phenomena in solid state fermentation[J]. Biochem Eng J，2004，17：15-26.

Kinetic models for alpha-pinene fermentation

REN Meng1，2，GAO Guo-fu1，*，XIAN Mo2，YANG Jian-ming2，*
（1.School of Life and Sciences，Nan Jing Agricultural University，Nanjing 210095，China；2.CAS Key Laboratory of Bio-based Material，Qingdao Institute of Bioenergy and Bioprocess Technology，Chinese Academy of Sciences，Qingdao 266101，China）

The dynamic models for alpha-pinene fermentation by Escherichia coli were studied.The kinetic models for cell growth ， alpha-pinene production and substrate consumption were proposed with Logistic equation ， Luedeking-Piret equation and Luedeking-Piret-Like equation though the optimal parameters estimation and nonlinear least-squares fitting method.The observed and estimated values of the models were in a good agreement， the result showed that the models could provide a reasonable description for the fermentation process of alpha-pinene.

α-pinene；fermentation kinetic model；fit.

Q851

A

1002-0306（2014）20-0196-04

10.13386/j.issn1002-0306.2014.20.034

2014－01－15

任萌（1988-），男，硕士研究生，研究方向：生物活性物质资源。

* 通讯作者：高国富（1963-），男，副教授，研究方向：生物活性物质资源。杨建明（1977-），男，副研究员，研究方向：生物催化。

国家自然科学基金（21206185，21376255）；国家高技术研究发展计划（SS2013AA050703-2）；国家科技支撑计划重大项目（2012BAD32B06-2）。