考虑风电场影响的电力系统支路脆弱性评估

陈 卓，李华强，周柯宇，许海青，黄昭蒙

（1.四川大学电气信息学院智能电网四川省重点实验室，成都610065；2.四川省电力公司成都电业局，成都610041）

风力发电作为可再生能源中发展最快的、最具有发展前景的一种发电方式，正日益走向规模化和产业化。大型并网风力发电场（简称风电场）成为风力发电的主流，在电力系统中发挥着越来越重要的作用。而风力发电的随机性及异步发电机组运行需要无功支持等显著的风电并网特点，都会对电力系统的安全稳定运行产生一系列影响[1-2]。电网脆弱性是指正常运行或受扰动、故障等影响下，电网承受干扰能力或传输能力可能呈现不断弱化趋势的特性[3]。随着风电并网规模不断扩大，电网结构变得更为复杂，可能会使电网脆弱性受到影响，进而影响系统稳定性。

在现有的国内外文献中，文献[4]对异步风力发电机组的模型进行了研究；文献[5]基于异步风力发电机模型，对并网风电场的最大注入功率进行计算分析；文献[6]研究了风电场无功补偿容量的确定，分析了风电场接入后电网的稳定性；文献[7]评估了大规模风电场对发输电系统可靠性的影响。而对电网脆弱性的研究主要分为两方面：文献[3]和文献[8，9]分别从能量函数、灵敏度技术、概率论基础上建立了脆弱性评估指标，用以研究电网元件的状态变量偏离正常状态或距离临界值的程度——状态脆弱性；文献[10，11]通过分别构建基于线路电抗的加权电网拓扑模型，基于P、Q 网分解的电网有向加权拓扑模型，从网络拓扑的角度研究某一单元在网络结构中的“重要程度”，即结构脆弱性。上述研究为含风电场的电网稳定性分析以及电网脆弱性评估的扩展和深入提供了极其重要的借鉴作用。

实际系统中判断一个元件是否脆弱，与其对网络结构的重要性和其运行状态易于受扰动或故障影响的程度都有密不可分的关系，二者兼顾才更符合电网实际情况。因此，本文综合考虑电网支路运行状态脆弱性和结构脆弱性，提出一组新的支路综合脆弱性评估指标，并由此对风电场接入电网的影响进行分析。首先建立风电场输出功率模型，确定采用常规潮流计算和异步发电机内部电路计算两部分交替迭代的方法来计算含风电场的电力系统潮流；其次由支路功率与节点电压建立支路静态能量函数模型，结合电气介数[13]加权，提出脆弱趋势指标和脆弱程度指标，综合反映支路在网络结构上的重要程度以及潮流、电压、发电机和负荷等的变化。以IEEE-30 节点系统为例加入风电场节点，对风电场接入前后、以及不同风速和不同接入点条件下的电力系统支路脆弱性仿真结果进行对比分析，评估了风电并网对电力系统脆弱性的影响，对实际风电并网规划具有一定参考意义。

1 风电场模型

1.1 风力发电机的输出功率模型

与常规发电机组不同，风力发电机组的输出功率主要由风速决定，二者间为非线性函数关系，表示[7]为

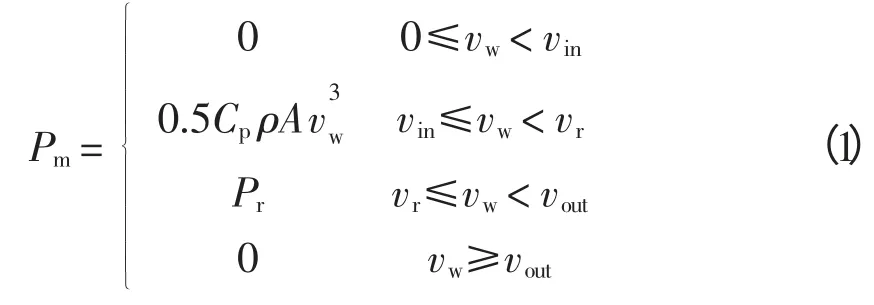
式中：vw、vin、vr、vout、Pr分别为风机的当前风速、切入风速、额定风速、切出风速和额定功率；Cp为与风机叶尖速比和桨距角有关的风能利用系数；ρ 为空气密度，kg/m3；A 为风机的扫掠面积，m2。

由式（1）可见，自然界的风能通过风机叶片转化为发电机转子上的机械功率Pm，根据确定的风速vw则可计算得Pm值。

1.2 异步发电机模型

由异步发电机原理可知，由于其定子电抗远小于励磁电抗，且定子电阻和铁心功率损耗可忽略，因此注入电网的有功功率Pw可视为与转子上的机械功率Pm相等，由此得到异步发电机Γ 型等值电路如图1[14]所示。

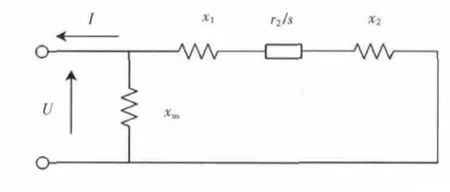
图1 单台异步发电机简化等值电路Fig.1 Simplified equivalent circuit of asynchronous generator

图中，U 为异步发电机机端电压，xm为励磁电抗，x1、x2分别为定子电抗和转子电抗，xk=x1+x2，r2为转子电阻，s 为滑差。根据图1 中所示电路连接关系，可得异步发电机有功功率和无功功率为

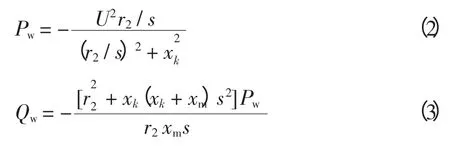
功率因数角正切为

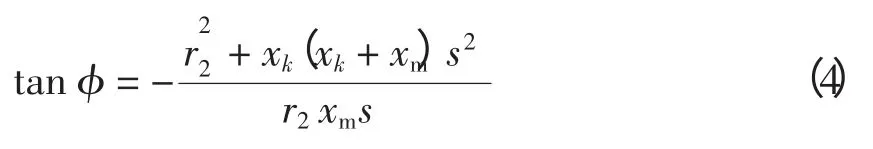
其中

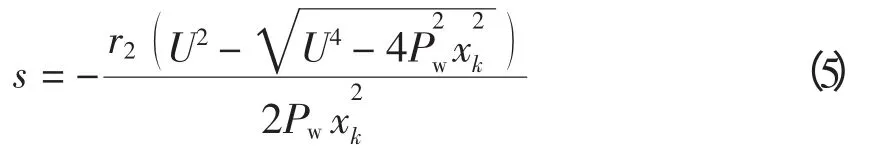
由式（3）可见，当异步发电机输出的有功功率Pw确定时，它吸收的无功功率Qw大小可由机端电压U、滑差s 求得。

1.3 含风电场的电力系统潮流计算

本文计算含风电场的电力系统潮流时[15]，将风电场整体接入电网同一个节点，暂不考虑尾流效应、地形因素等对风电机组之间的相互影响，但不可忽略风电机组的以下特点：异步发电机其本身不具备励磁调节装置，没有电压调节能力，因此不可将它视为电压幅值恒定的PV 节点；异步发电机向系统注入有功功率时会从系统吸收无功功率，且吸收无功的大小与其机端电压、有功输出以及滑差值成一定的函数关系，故也无法把它简单处理为恒定功率的PQ 节点[14]。

鉴于上述原因，本文采用将异步发电机内部电路计算和电力系统潮流计算交替迭代的方法：由发电机等值电路求得风电场输出的有功和吸收的无功，代入电力系统计算潮流，再将所得潮流结果代回发电机等值电路进行下一次计算。具体步骤如下：

（1）读入风电场风速vw，根据式（1）计算风电场输出有功功率Pw=Pm；

（2）设定风电场电压初值Us；

（3）由Pw、Us，根据式（5）计算滑差s；

（4）由式（3）计算风电场吸收的无功功率Qw；

（5）把风电场看作PQ 节点并入系统，利用电力系统常规潮流计算，求出风电场节点电压U；

（6）判断，若U≠Us，令Us=（U + Us）/2，返回（3）～（5）继续执行，直到|Us-U|＜ε 为止（ε=10-5）。

2 基于静态能量函数和电气介数的支路脆弱性综合评估指标

2.1 支路静态能量函数模型

支路能量能综合体现支路功率输送量的变化在能量积累上的映射，包括有功功率与无功功率传输对应的两部分势能[11]。这里在文献[16]所建节点能量函数模型基础上，构建支路静态能量函数模型。其中，支路两节点间的电压相角差决定其有功功率传输，而电压幅值差则决定支路的无功功率传输，所以同时对电压相角差和电压幅值差两部分进行积分，则可求得支路能量函数[3]。

根据图2 所示支路模型，支路节点i、j 间的电压幅值差为

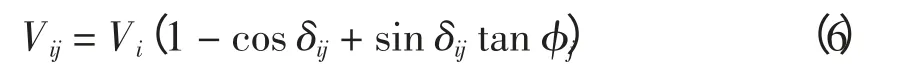
式中：Vi为支路节点i 的电压幅值；δij为节点i、j 间的相位差；φj为节点j 的功率因数角。

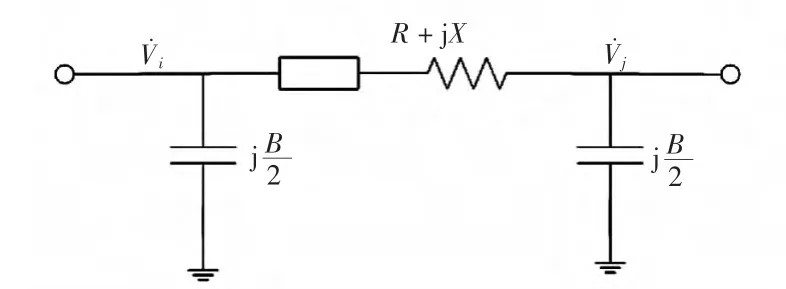
图2 电网支路等值电路Fig.2 Equivalent circuit of power network branch

由此建立节点i、j 间支路能量表达式为

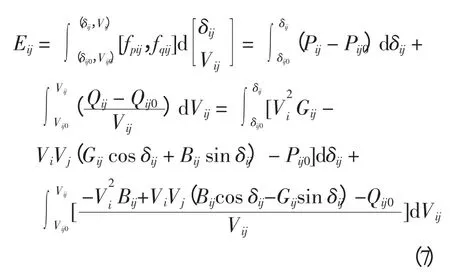
式中：Gij、Bij分别为支路ij 的电导和电纳；Pij、Qij分别为支路ij 在当前运行状态下的有功功率和无功功率传输量；Vij0、δij0、Pij0、Qij0分别为Vij、δij、Pij、Qij的初始状态值。将式（6）代入式（7），可求得支路静态能量函数值。

根据静态能量函数的数学模型在支路功率传输方程基础上构建的式（7），量化了从初始运行状态变化到当前运行状态时，支路上传输的功率变化量对应的能量积累。若将多母线系统的节点编号代入节点i 和j，式（7）即可推广到多母线系统中表示任一支路能量函数。

2.2 支路的电气介数

大多数复杂网络模型基于潮流沿最短路径传播的假设，将介数作为指标来评估网络的结构脆弱性。其局限在于只考虑最短路径，片面扩大了其在功率传播中的重要性，而忽略其他路径的影响，不符合电力系统的物理实际。为此提出支路ij 的电气介数（electric betweenness）Bij[13]，即

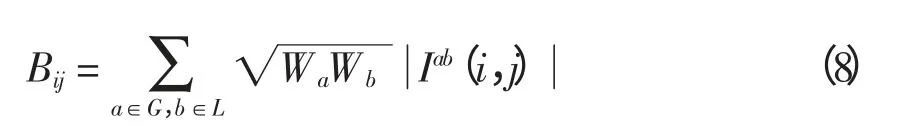
式中：Wa为发电机节点a 的权重，取发电机额定容量或实际出力；Wb为负荷节点b 的权重，取实际或峰值负荷；G 和L 分别为发电节点、负荷节点的集合；Iab（i，j）表示向“发电-负荷”节点对（a，b）间注入单位电流元后，在线路（i，j）上引起的电流。

Bij综合考虑发电和负荷节点的权重，将支路在全网潮流传输中的贡献量化，对线路的承载能力及其在网络中的活跃程度进行有效反映，可用于筛选系统中的关键支路。传统加权介数假设潮流只按最短路径传输，而电气介数的计算基于电路方程，因而比前者更符合电网实际。

2.3 基于静态能量函数和电气介数的支路脆弱性综合评估指标

2.3.1 支路脆弱趋势指标

根据系统脆弱性的定义，提出支路脆弱趋势指标表达式为

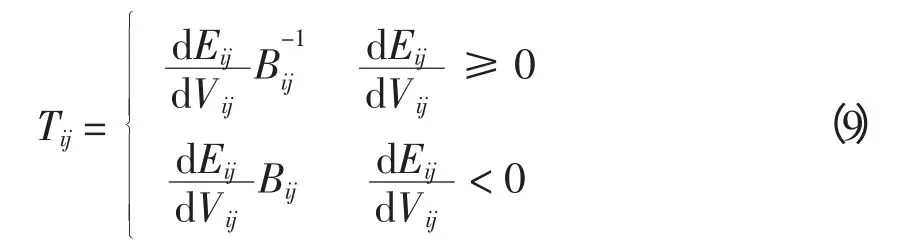
随着系统结构和支路传输任务的改变，各条支路均会呈现出脆弱趋势，但其脆弱趋势的表现不同。

综上所述，根据脆弱趋势指标的物理意义，可得Tij越小，支路更容易表现出脆弱趋势。

采用Tij作为支路脆弱趋势评估指标，不仅全面量化了支路状态脆弱性受其功率传输和节点电压幅值相角的影响，同时有效反映了支路在网络拓扑结构中的重要程度。

2.3.2 支路脆弱程度指标

为更好地对比电网接入风电场后支路脆弱程度的变化，提出脆弱程度指标为

式（10）中，Cij能够度量在不同风速情况下，支路能量逼近其能量极限的裕度与其初始能量裕度的比值，即状态脆弱程度，加权后，从结构角度对支路状态脆弱程度进一步放大，能更完整地反映系统中任一支路在当前风速和接入点情况下对应运行状态和结构的综合脆弱程度。

当风电场接入电网，系统结构和潮流发生改变，Cij越小，表明系统运行在当前状态下，该支路能量更逼近其能量极限边界，支路在状态上更脆弱；若越小，则该支路在全网潮流传输中贡献更大，在结构上更脆弱；Cij加权后，使得相同状态脆弱程度的线路中，结构上更活跃者的Kij更小，支路传输功率的脆弱程度更深。

综上所述，本文拟采用脆弱趋势指标Tij来筛选脆弱支路，用脆弱程度指标Kij来判断支路脆弱严重程度，并将两者结果相结合来综合评估支路的脆弱性，物理意义清晰，判据简单实用。

3 算例仿真

风电场经变压器和110 kV 线路接入IEEE-30节点系统，如图3 所示。应用Matlab 编程实现该系统的仿真计算。

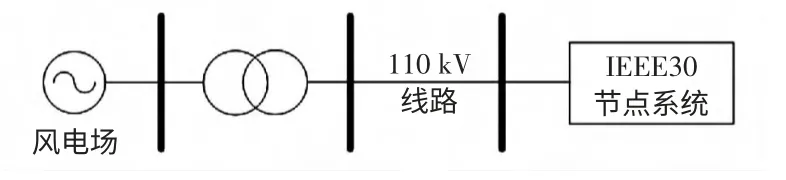
图3 风电场接入IEEE-30 节点系统Fig.3 Wind farm connected to IEEE-30 system

风电场由50 台风机组成，单台风机容量为600 kW，场中风电机组分为5 排，横向、纵向间距分别为120 m 和150 m，叶轮高50 m；风电场空气密度取1.235 kg/m3，风机的扫掠面积为1 800 m2，风机切入、切除、额定风速分别为3 m/s、25 m/s、14m/s；风电机组低压侧基准电压为0.69 kV，风电场接入系统的线路等效阻抗标幺值为0.104 1+j0.206 3。

经交替迭代计算，得风速–功率关系如表1所示（以接入26 号节点为例）。

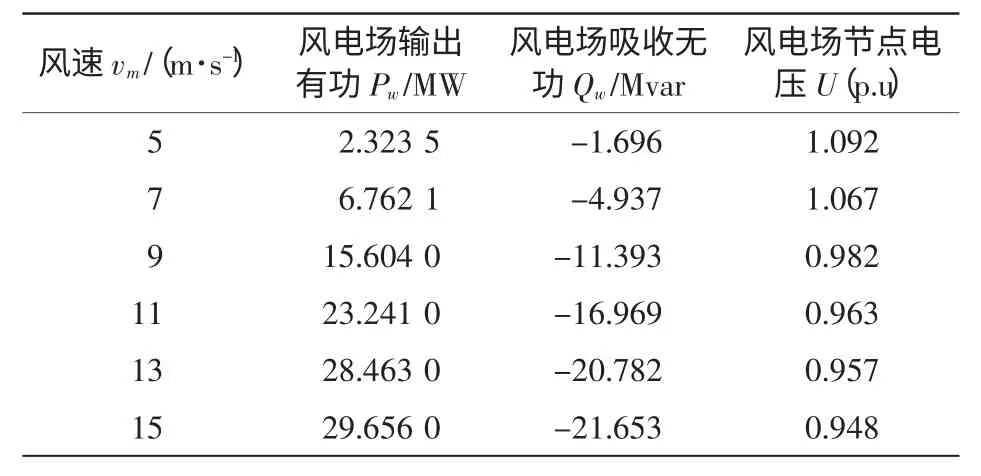
表1 风电场风速-功率关系Tab.1 Realpower，reactivepowerandvoltageofwindfarm

表2 为风电场接入前、风电场接入26 号节点后不同风速下的支路脆弱趋势指标值，因篇幅有限，仅列出按照本文指标判断的脆弱趋势较明显的几条支路。

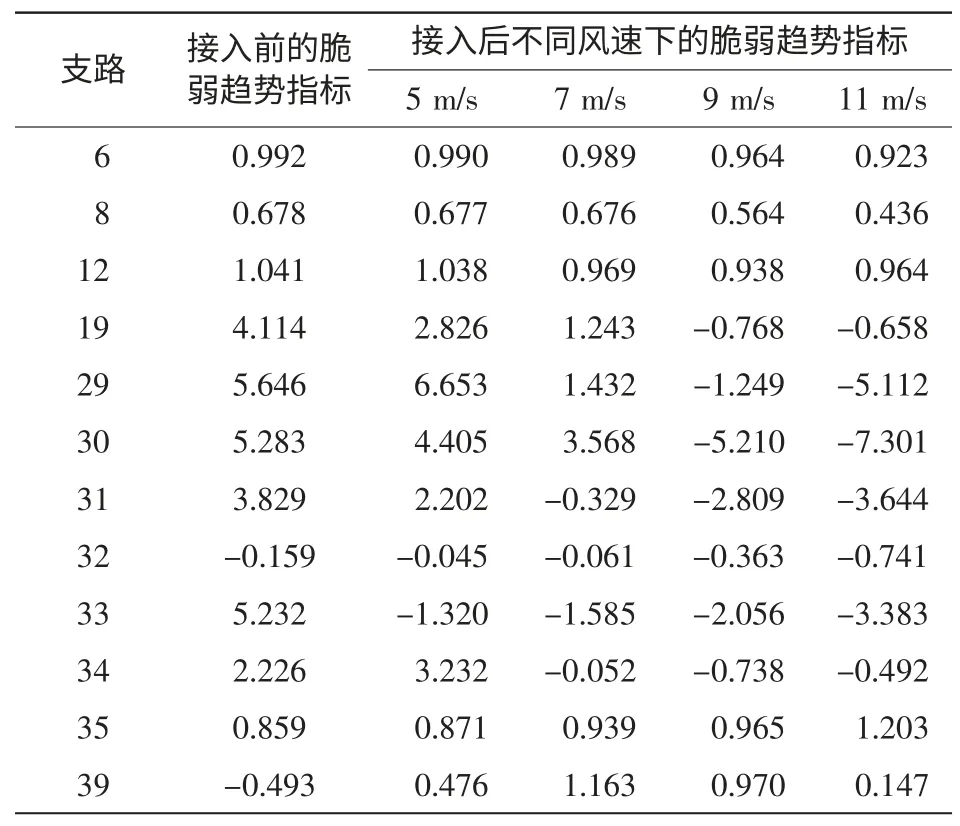
表2 风电场接入前后的支路脆弱趋势指标Tab.2 Vulnerable branch before and after wind farm connected to the system

由表2 可知，风电场接入前，原系统支路6、8、12、32、35、39 的脆弱趋势指标值明显小于其他支路；随着风电场接入，风速增大，脆弱趋势明显的支路逐渐增多。其原因在于风电场并网后改变了电网结构，其从电网吸收无功功率的特性使得系统的无功负担加重，支路更容易表现出脆弱趋势。其中，支路6、8、39 距离发电机较近，承担着由发电机向系统注入的能量，且能量变化量均较大，导致该类支路脆弱；支路12 为变压器支路，支路19、28、29、30、31、32、33、34、35 都是带负荷的末端支路，传输任务重，因此这类支路易表现出更明显的脆弱趋势。

但支路脆弱趋势指标值并不全都随着风速的增大而一直减小，如支路19 的脆弱趋势指标值就是先增大再减小。这是因为风电场出力和负荷需求变化会引起系统的潮流分布和运行状态改变，这种变化还受系统结构影响，故并非简单的线性关系。

根据表3 数据可见，随着风速增加，支路脆弱程度指标值普遍减小，表明支路的脆弱程度会随着风速增大而加深。这是因为风速越大，风电场从电网吸收无功越多，导致系统支路电压和能量波动越大。说明本文所提的脆弱程度指标与风速的增长存在相应的递减关系，即该指标能准确地反映在不同风速条件下的支路脆弱程度。

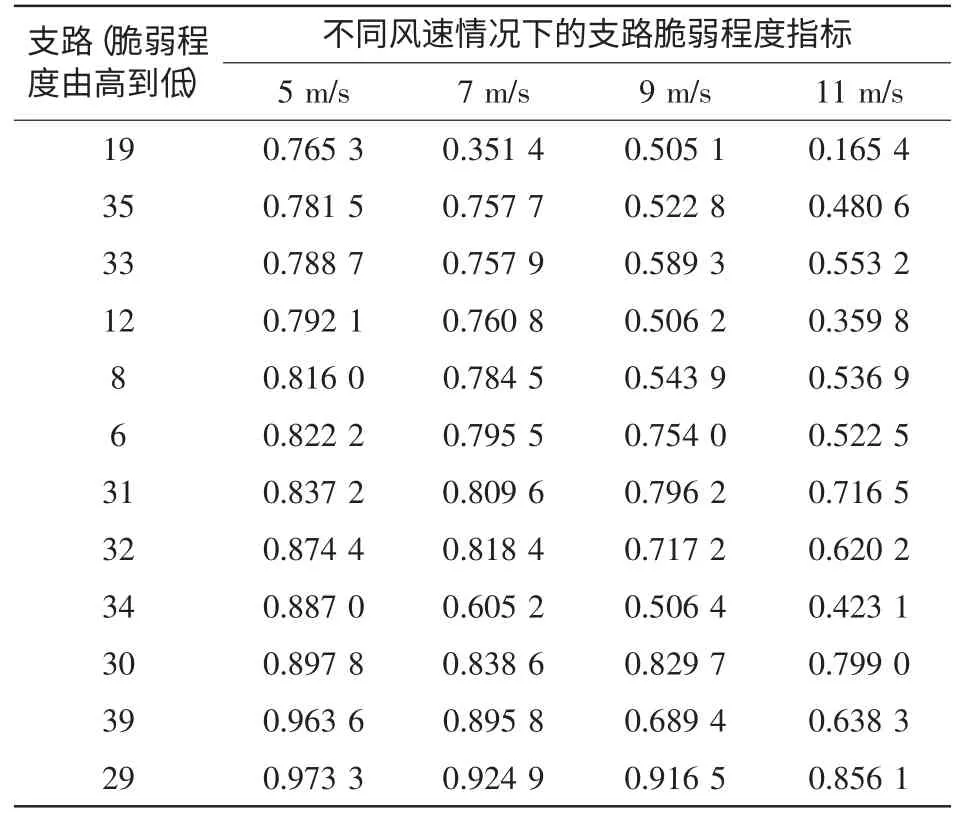
表3 不同风速条件下的支路脆弱程度Tab.3 Branchvulnerabilitydegreeatdifferentwindspeeds

此外，在接入点附近的支路32、33、34 的脆弱程度对风速变化的波动幅度较其他支路更大，因此在实际风电并网中，为了提高并网后系统的稳定性，有必要在接入点进行适当的无功补偿。

将风电场分别接入系统所有节点进行仿真，汇总比较支路脆弱趋势和脆弱程度。限于篇幅，表4 仅列出带无功补偿的两个并网点，以及对系统影响分别最大、最小的并网点。

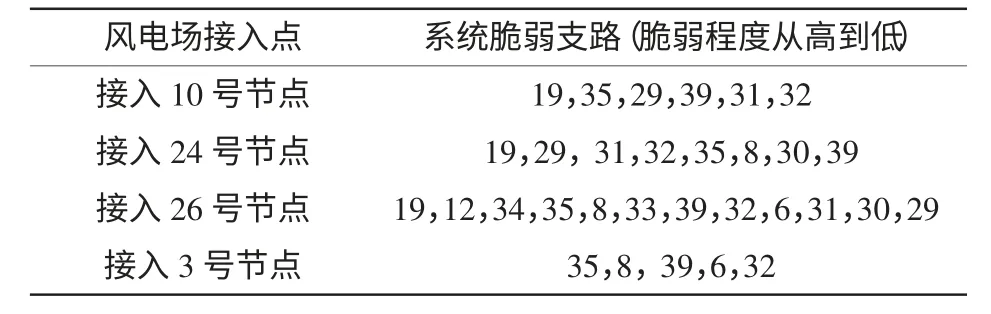
表4 风电场接入不同节点后的支路脆弱性（风速9 m/s）Tab.4 Branch vulnerability assessment at different connecting points（at 9 m/s）

结果表明接入点不同，系统脆弱支路不同，且排序不尽相同；但是几条重要脆弱支路35、8、39的相对排序不变。原因在于接入点不同，对系统结构和潮流分布的改变不同，故对系统支路脆弱性的影响不同。

同时，节点10 和节点24 都是原系统的无功补偿点，风电场接入此类节点能够在一定程度上减小对系统脆弱性影响；但因补偿量不同，且两节点的电气介数不同，即在电网拓扑结构中的重要程度不同，故接入节点10 与节点24 的支路脆弱性不同。

此外，对比所有接入点的仿真结果，可发现接入节点30 时，系统脆弱支路最多，且脆弱程度普遍较深，对电网脆弱性影响最大。究其原因是该节点为带负荷的系统末端节点，传输任务较重，电压水平较低，将风电场并入此类节点，无疑比接入其他节点对系统的扰动更大，因此实际规划风电场并网时应避免选择这类节点作为并网点。

而接入点选在节点3 时，系统支路脆弱性在所有接入点中最低，这是因为该节点邻近发电机节点，电压水平较高，且拓扑结构中位置较为独立，承担的传输任务较轻，故加入此节点对电网脆弱性影响最小。

4 结论

本文克服目前的脆弱性研究不能兼顾元件实时运行情况和网络拓扑结构的不足，将支路静态能量函数模型和电气介数进行有效结合，建立了综合考虑支路的状态参数和结构参数的支路脆弱性评估指标，更符合电力系统实际情况，且物理意义清晰，计算速度快。

经过对风电场接入前后、以及不同风速、不同接入点情况下系统支路脆弱性仿真结果对比分析表明：

（1）风电场接入后，将改变电网拓扑结构和潮流分布，进而增大电网的支路脆弱性；

（2）风速增加时，风电场从电网吸收更多的无功功率，对电网扰动更大，因而脆弱支路随风速增大而增多，且脆弱程度普遍加深；

（3）风电场接入点附近支路脆弱性波动更大；

（4）风电场接入点不同，对电网潮流分布和拓扑结构的改变不同，故对支路脆弱性的影响结果也会变化。

这些结论，对于风电场接入电力系统的规划以及稳定运行具有一定的指导意义。本文风电场模型暂未考虑尾流效应、地形因素等对风电机组之间的相互影响，可能与实际情况有一定误差，今后可就此进行更深入完善的研究。

[1]陈树勇，戴慧珠，白晓民，等（Chen Shuyong，Dai Huizhu，Bai Xiaomin，et al）.风电场的发电可靠性模型及其应用（Reliability model of wind power plants and its application）[J].中国电机工程学报（Proceedings of the CSEE），2000，20（3）：26-29.

[2]孙涛，王伟胜，戴慧珠，等（Sun Tao，Wang Weisheng，Dai Huizhu，et al）.风力发电引起的电压波动和闪变（Voltage fluctuation and flicker caused by wind power generation）[J].电网技术（Power System Technology），2003，27（12）：62-66，70.

[3]刘群英，刘俊勇，刘起方（Liu Qunying，Liu Junyong，Liu Qifang）.基于支路势能信息的电网脆弱性评估（Power grid vulnerability assessment based on branch potential energy information）[J].电力系统自动化（Automation of Electric Power Systems），2008，32（10）：6-11.

[4]Petru T，Thiringer T. Modeling of wind turbines for power system studies[J].IEEE Trans on Power Systems，2002，17（4）：1132-1139.

[5]吴俊玲，周双喜，孙建锋，等（Wu Junling，Zhou Shuangxi，Sun Jianfeng，et al）.并网风力发电场的最大注入功率分析（Analysis on maximum power injection of wind farm connected to power system）[J].电网技术（Power System Technology），2004，28（20）：28-32.

[6]田春筝，李琼林，宋晓凯（Tian Chunzheng，Li Qionglin，Song Xiaokai）.风电场建模及其对接入电网稳定性的影响分析（Modeling and analysis of the stability for the power system considering the integration of the wind farms）[J].电力系统保护与控制（Power System Protection and Control），2009，37（19）：46-51.

[7]张硕，李庚银，周明（Zhang Shuo，Li Gengyin，Zhou Ming）.含风电场的发输电系统可靠性评估（Reliability assessment of generation and transmission systems integrated with wind farms）[J].中国电机工程学报（Proceedings of the CSEE），2010，30（7）：8-14.

[8]孟绍良，吴军基，王虎（Meng Shaoliang，Wu Junji，Wang Hu）.电网脆弱性评价的灵敏度分析法（Power grid vulnerability assessment based on sensitivity analysis）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（5）：89-93.

[9]陈为化，江全元，曹一家，等（Chen Weihua，Jiang Quanyuan，Cao Yijia，et al）. 基于风险理论的复杂电力系统脆弱性评估（Risk-based vulnerability assessment in complex power systems）[J]. 电 网 技 术（Power System Technology），2005，29（4）：12-17.

[10]丁明，韩平平（Ding Ming，Han Pingping）.加权拓扑模型下的小世界电网脆弱性评估（Vulnerability assessment to small-world power grid based on weighted topological model）[J]. 中 国 电 机 工 程 学 报（Proceedings of the CSEE），2008，28（10）：20-25.

[11]魏震波，刘俊勇，李俊，等（Wei Zhenbo，Liu Junyong，Li Jun，et al）.基于P、Q 网分解的有向加权拓扑模型下的电网脆弱性分析（Vulnerability analysis of electrical power network under a directed-weighted topological model based on the P-Q networks decomposition）[J]. 电力系统保护与控制（Power System Protecting and Control），2010，38（24）：19-22，29.

[12]魏震波，刘俊勇，朱国俊，等（Wei Zhenbo，Liu Junyong，Zhu Guojun，et al）.基于电网状态与结构的综合脆弱评估模型（A new integrative vulnerability evaluation model to power grid based on running state and structure）[J]. 电力系统自动化（Automation of Electric Power Systems），2009，33（8）：11-14，55.

[13]徐林，王秀丽，王锡凡（Xu Lin，Wang Xiuli，Wang Xifan）.电气介数及其在电力系统关键线路识别中的应用（Electric betweenness and its application in vulnerable line identification in power system）[J]. 中国电机工程学报（Proceedings of the CSEE），2010，30（1）：33-39.

[14]王海超，周双喜，鲁宗相，等（Wang Haichao，Zhou Shuangxi，Lu Zongxiang，et al）.含风电场的电力系统潮流计算的联合迭代方法及应用（A joint iteration method for load flow calculation of power system containing unified wind farm and its application）[J]. 电网技术（Power System Technology），2005，29（18）：59-62.

[15]Feijoo A E，Cidras J. Modeling of wind farms in the load flow analysis [J]. IEEE Trans on Power Systems，2002，15（1）：110-115.

[16]刘慧，李华强，郑武，等（Liu Hui，Li Huaqiang，Zheng Wu，et al）.基于电压脆弱性的支路事故排序快速算法（Fast algorithm of branch contingency ranking based on voltage vulnerability）[J]. 电力系统保护与控制（Power System Protection and Control），2010，38（23）：177-181.