基于改进PSO 算法的电力系统无功优化
2014-03-02陈前宇陈维荣戴朝华张雪霞
陈前宇,陈维荣,戴朝华,张雪霞
(西南交通大学电气工程学院,成都610031)
无功优化问题是典型非线性规划问题,具有多目标、多约束、连续变量和离散变量同时存在的特点[1,2],传统的算法如线性规划法、非线性规划法、内点发、牛顿法[3~5]等在求解无功优化的离散变量规整和多峰多极值问题时具有一定的局限性[6]。近年来,遗传算法、蚁群算法、粒子群优化PSO(particle swarm optimization)算法等智能优化算法在无功优化中得到了成功运用。其中,PSO 算法由于具有简单易行、收敛速度快、优化效率高、鲁棒性好等优势,在处理非线性问题中取得了很好的效果[7],但其不足在于易于陷入局部最优解[8]。
针对PSO 算法易于陷入局部最优的缺点,很多文献提出了改进的PSO 算法。文献[8]考虑其他粒子的历史最优信息使得搜索方向多样化。文献[9]提出一种动态调整种群规模的方法以更好地适应进化,该算法可以较好地避免PSO 算法过快收敛于局部最优解。文献[10]提出的随机聚焦粒子群优化SFPSO(stochastic focusing particleswarm optimization)算法使粒子并不同时向种群中的全局极值和个体极值趋进,而是在全局极值的一个邻域中进行搜索,以避免粒子陷入局部最优。文献[11]提出的自适应聚焦粒子群优化AFPSO(adaptive focusing particle swarm optimization)算法使平衡点更新更加频繁,提高了算法的搜索效率。本文借鉴部分已有的改进算法,针对PSO 算法易于陷入局部最优,对PSO 算法进行以下方面的改进:分阶段调节加速因子与动态调整惯性权重,以很好地平衡全局搜索和局部寻优的关系;每次迭代后,使部分性能较差的粒子朝本次迭代中性能最好的粒子运动,若粒子性能变得更好,则该粒子继续保持该速度搜索,粒子的某维位置超出了规定的范围,则将粒子的该维位置返回至上次迭代处,改进后的算法称为多策略融合自适应粒子群优化MSI-APSO(adaptive particle swarm optimization with multistrategy integration)算法。
将本文的MSI-APSO 算法运用到电力系统无功优化上,对IEEE 30 节点系统中进行仿真试验,并与其他一些改进的PSO 算法的优化结果进行比较。
1 电力系统无功优化数学模型
1.1 目标函数和惩罚因子
目标函数为
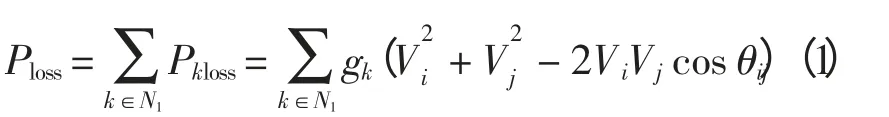
采用罚因子后有
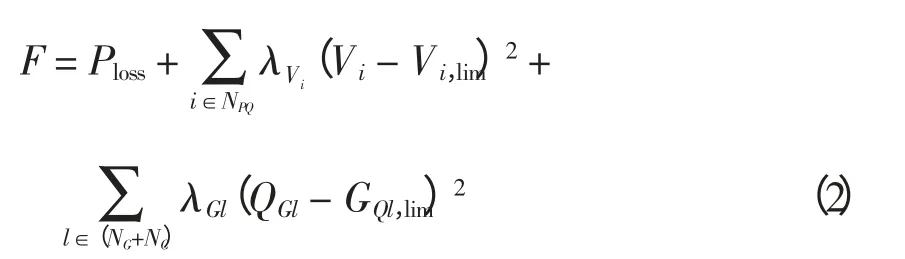
式中:N1表示系统参与损耗计算支路的条数;gk为节点i、j 之间支路电导;Vi、Vj分别为节点i、j 的电压模值;θij表示i、j 节点电压相角差;λVi和λGl为罚因子;Vi,lim和GQl,lim可表示为

式中:Vi,max、Vi,min分别为节点电压的上下限值;QGl,max、QGl,min分别为各发电机发出无功功率的上下限值。
1.2 等式约束
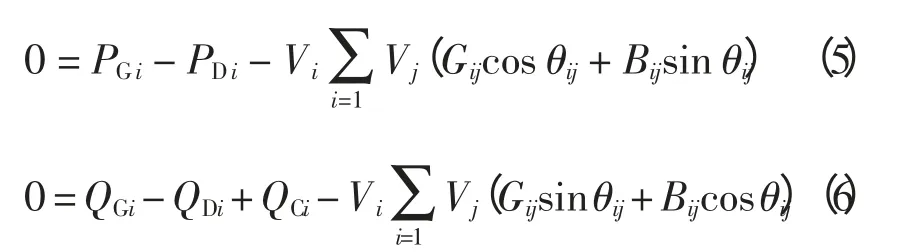
式中:PGi、QGi、PDi、QDi分别表示节点i 对应发电机发出的有功功率、无功功率、节点i 对应负荷有功功率和无功功率;QCi为电容器/电抗器无功补偿功率;Gij、Bij表示节点导纳矩阵的实部和虚部。
1.3 不等式约束
控制变量约束条件为
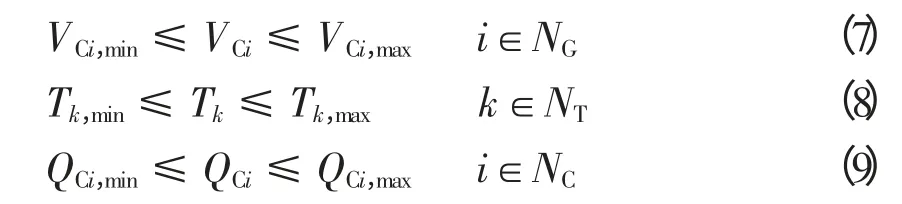
式中:VGi为发电机的端电压;Tk为可调变压器变比;NG、NT、NC分别为系统发电机节点数、有载变压器数和无功补偿数。
状态变量的约束为

式中:QCi为节点i 对应发电机发出的无功功率;Vi为第i 个PQ 节点的电压模值;ND为负荷节点数。
2 改进的PSO 算法
2.1 标准PSO 算法
PSO 算法是由Kennedy 和Eberhart 于1995年提出的一种基于群体智能的全局优化进化算法。该算法最初是在二维空间对鸟类觅食过程中迁徙和群聚生物智能行为的模拟。由于实际系统的多维性,后来又发展到了D 维空间,搜索空间中粒子的位置就是每个优化问题的一个潜在解,粒子通过一定的速度在搜索空间中寻优,这个速度源于其自身的经验总结和优良信息的传递。
本文将第i 个粒子在解空间的位置记为xi=[xi1,xi2,…,xid,…,xiD],粒子的速 度 记为vi=[vi1,vi2,…,vid,…,viD],fxi为每个粒子位置适应值,同时,每个粒子拥有一个历史最好位置pi=[pi1,pi2,…,pid,…,piD]和粒子现在的位置(xi)。通过粒子之间pi适应值的比较,适应值最小(目标函数是最小化问题)的位置即为pg=[pg1,pg2,…,pgD],即种群中目前最佳位置。粒子在搜索空间中,每一次搜索均追随个体历史最佳位置和群体历史最佳位置,通过这两个最佳位置为粒子的搜索指明方向。
在粒子的第t+1 次迭代中,每个粒子的每一维速度和位置更新为
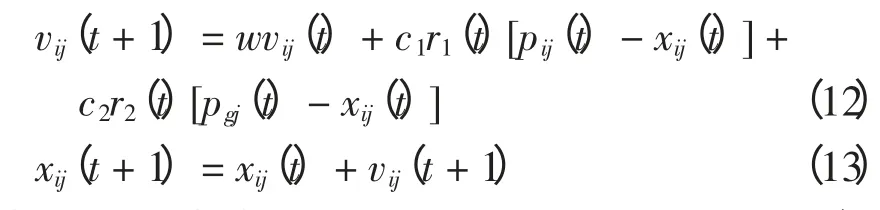
式中:w 为惯性权重;c1、c2为加速因子;r1、r2为(0,1)之间的随机数。
2.2 MSI-APSO 算法
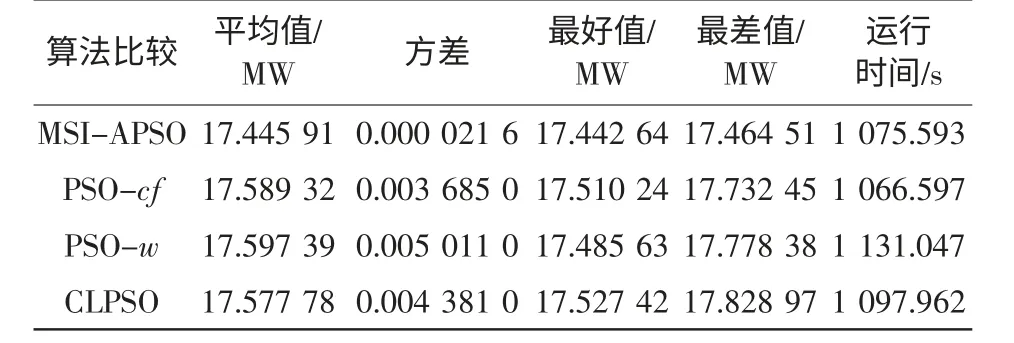
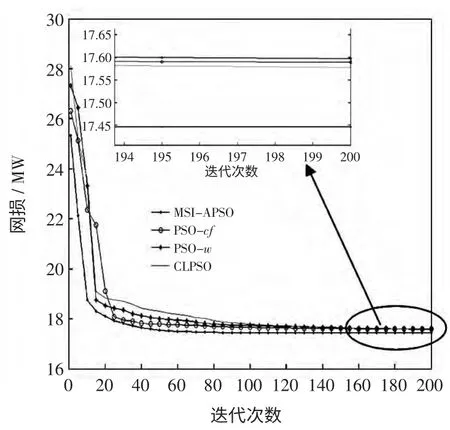
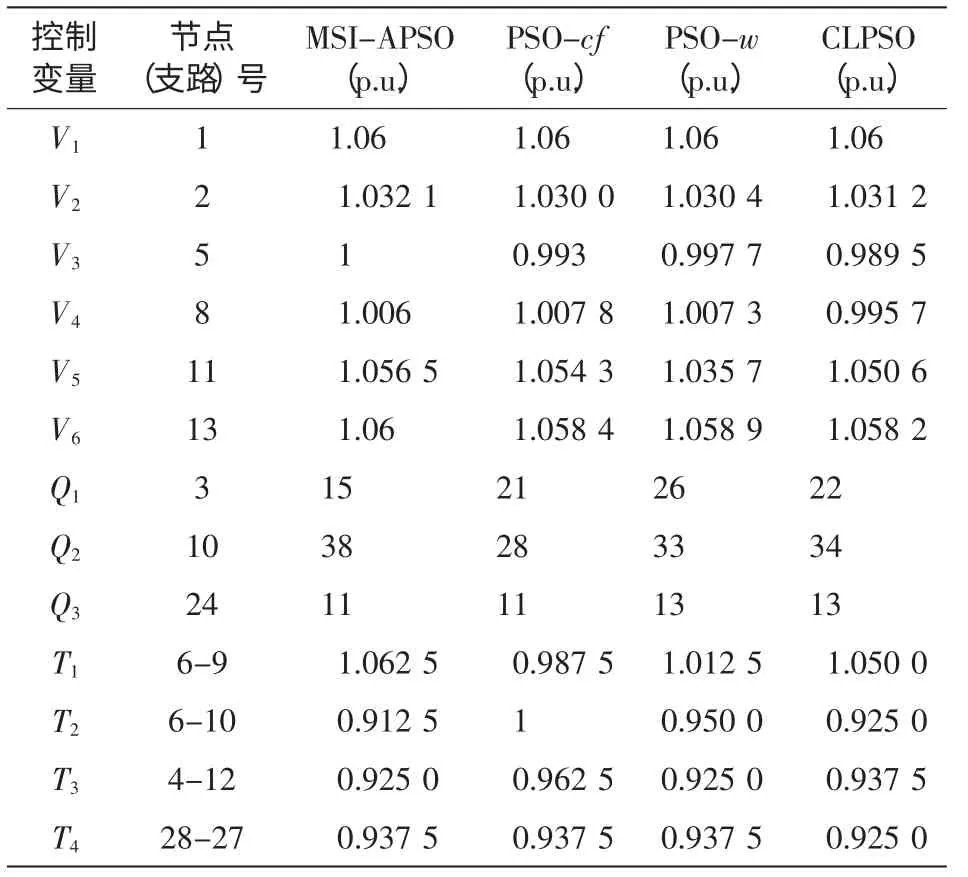
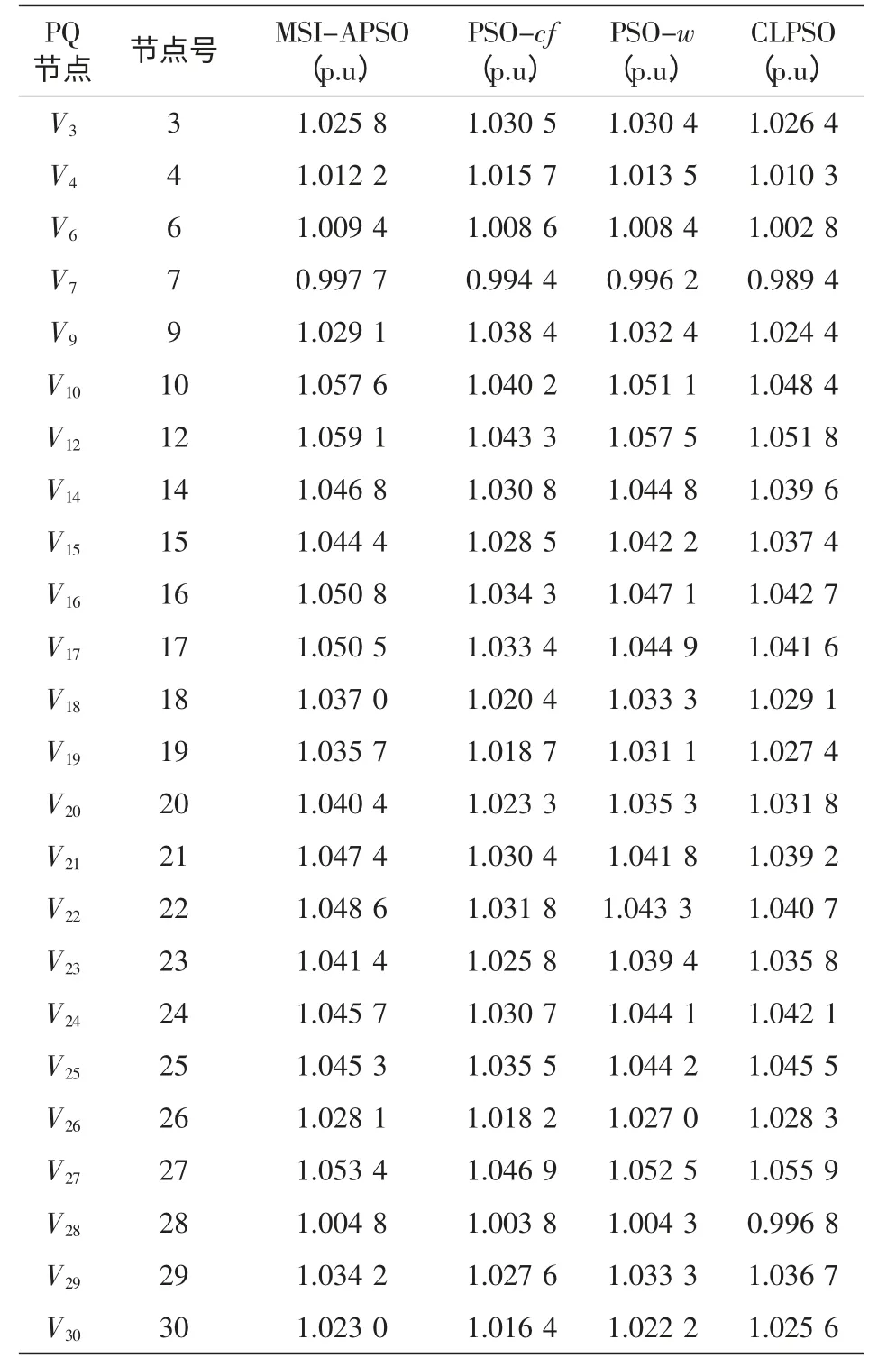
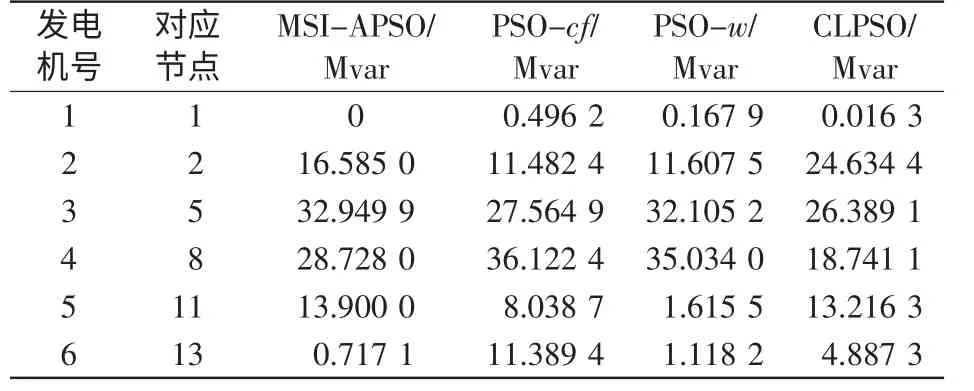
加速因子c1和c2用于调整粒子“自身经验”与“群体经验”以对其速度更新。标准版PSO 算法通常取c1=c2,粒子朝向两个“最佳位置”运动时的权重相同,没有考虑粒子各个搜索阶段搜索的重点。本文的MSI-APSO 算法采用分阶段调整加速因子,粒子在搜索前期主要跟随个体历史最佳位置pi,粒子的个体导向因素占据主要作用,在这一阶段粒子充分探索自己周围的区域,在保持个体自身快速开发能力的同时,保持群体多样性和较好的全局探索能力;在搜索的后期,粒子主要跟踪种群历史最佳位置,进行集中搜索,加快收敛速度能力的同时,保持全局的搜索精度,这一阶段粒子的全局导向起主要作用[8]。采用的更新策略为:当t 惯性权重w 保持粒子运动惯性,使其具有扩展探索空间的趋势。较大的惯性权重将使粒子具有较大的速度,从而有较强的探索能力;较小的惯性权重将使粒子具有较强的开发能力,动态调节惯性权重有利于平衡粒子的全局搜索和局部开发的关系,本文的MSI-APSO 算法根据粒子各自的个体历史最佳位置与种群历史最佳位置的关系自适应调节惯性权重,即 式中:fpi(t)为第i 个粒子个体历史最佳位置的适应值;fbest(t)为种群历史最佳位置的适应值;N 为种群中粒子个数;r 为(0,1)之间的常数。该方法区分文献[13]的动态调节惯性权重的策略是将粒子的个体历史最佳位置适应值与种群历史最佳位置适应值的“距离”作为惯性权重调节依据,该“距离”表征粒子的个性与共性的接近程度,“距离”越小,惯性权重减小,粒子进行集中搜索,增大其局部开发能力;“距离”越大,惯性权重增大,扩大其全局开发能力。 改善部分性能差的粒子,使部分个体历史最佳位置适应值较大的粒子朝向该次迭代中性能最好(种群历史最佳位置)的粒子运动,这有利于算法快速收敛。即:设[Fp1,Fp2,Fp3,…,Fpi,…,FpN]为个体历史最佳位置适应值按从小到大的排序,其对应个体历史最佳位置为[p1,p2,p3,…,pi,…,pN]。 式中,m 为待改善粒子的个数。 对于每个粒子而言,迭代后,若粒子的适应值比该粒子的个体历史最佳位置适应值更小,说明粒子以该速度搜索更有利于找到全局最优值,于是可以保持这个速度继续搜索下去。即 该方法区分文献[10]所提速度位置更新方式在于判断粒子第t-1 次位置更新后搜索效果与t-2次的个体历史最佳位置适应值比较,若比较后前者效果较好,则下次可沿此速度搜索下去。 若每次迭代后粒子的位置超出了规定的搜索范围,则将粒子的该维位置返回到上次迭代处,这样避免了粒子总在边界上搜索,造成粒子难以跳出边界值的后果。即 罚函数处理约束条件时,罚因子的选取是一个复杂的过程:罚因子过小,可能过分搜索不可行域,导致得到可行解的收敛时间过长,甚至得不到可行解;罚因子过大,可能没有充分搜索不可行域,容易陷入局部极值。因此,本文采用随迭代次数线性递增罚因子的方法来处理状态变量越界的问题。罚因子经过多次测试选取以保证各状态变量不会越界。MSI-APSO 算法中连续变量和离散变量混合处理,然后对离散变量取整,潮流计算采用牛顿拉夫逊法,于是基于MSI-APSO 算法的无功优化的步骤如下。 步骤1 原始数据的输入。 输入包括MSI-APSO 算法的种群数、最大迭代次数、粒子的维数、加速因子。读入控制变量和状态变量的取值范围、各节点的负荷功率以及系统支路的参数等。 步骤2 对粒子进行初始化。 (1)初始粒子的位置每维计算公式为 (2)粒子速度的最大步长一般设置为 (3)初始粒子的速度每维计算式为 步骤3 求解个体适应度值。 由于可调变压器变比、各节点无功补偿量是离散变量,而粒子群优化算法是在连续空间的搜索,因此,求解适应度值之前,先需要对控制变量中离散变量进行离散化,即 式中:k 为在MSI-APSO 算法中没被离散化前的变压器变比;kmin为变压器变比的下限值;lk为变压器分接头调节步长;Tki为离散后的变压器变比;round(·)函数表示对数据的四舍五入取整;Q为在MSIAPSO 算法中没有被离散化前的电容器/电抗器无功补偿功率;Qmin为电容器/电抗器无功补偿功率的下限值;lQ为无功补偿的调节步长;QCi为离散后的电容器/电抗器无功补偿功率。 然后,把进行离散化后的控制变量及连续变量带入测试系统,进行潮流计算,计算网络损耗,然后按式(2)采用罚函数对越界量进行处理,计算粒子的适应值fxi,并将此时各个粒子的位置记为各自的初始个体极值pi,适应值最小的位置记为初始全局极值gbest。 步骤4 更新个体极值和全局极值。 更新个体极值:若fxi<fpi,则令fpi=fxi,pi=xi,否则,pi不变;更新全局极值:若fpi<fbest,则令gbest=pi,否则gbest不变。 步骤5 粒子的速度和位置更新。 运用第2.2 节中的MSI-APSO 算法更新粒子的位置xi和速度vi。 步骤6 迭代计算。 重复步骤3~步骤5,判断结果是否达到收敛精度或者满足最大迭代次数,若是,则输出结果;否则,继续循环计算。 本文采用IEEE30 节点系统进行测试,该系统包含41 条支路、21 个负荷节点、6 台发电机、4 条可调变压器支路、3 台并联电容器。21 个负荷节点分 别 在 节 点2,3,4,5,7,8,10,12,14,15,16,17,18,19,20,21,23,24,26,29,30。6 台发电机在节点1,2,5,8,11,13。4 台可调变压器在支路6~9、6~10、4~12、28~27。3 台并联电容器在节点3,10,24。参数详见matpower4.1 中IEEE30 文件[14,15]。取补偿电容器无功补偿量调节步长为1Mvar,可调变压器变比步长为0.0125。 IEEE30 节电系统发电机参数上下限值见表1。并联电容器补偿无功功率上下限值如表2 所示。各节点电压和变压器变比上下限值如表3 所示。 表1 发电机参数及其上下限值Tab.1 Parameters and their limitations of generation 表2 并联电容器补偿无功功率上下限值Tab.2 Reactive power compensation limitations of Shunt capacitor 表3 各节点电压和变压器变比上下限值Tab.3 Limitations of bus voltages and transformer taps 初始条件下,各节点无功功率补偿电容量设置为0,各发电机端电压为1.0 p.u.,变压器变比为1.0。系统总的负荷量为Pload= 284.3 MW,Qload=126.2 Mvar,系统总损耗Ploss= 20.88 MW,Qloss=81.02 Mvar。 在初始状况下,有11 个PQ 节点电压越限,分别为:节点18 电压为0.934 p.u.、节点19 为0.930 p.u.、节点20 为0.934 p.u.、节点21 为0.936 p.u.、节点22 为0.936 p.u.、节点23 为0.932 p.u.、节点24 为0.924 p.u.、节点25 为0.933 p.u.、节点26 为0.914 p.u.、节点29 为0.927 p.u.、节点30 为0.914 p.u.。4 台发电机无功功率越限,平衡节点1 对应发电机无功功率为-59.49 Mvar,节点2 为51.05 Mvar,节点5 为63.31 Mvar,节点8 为83.3 Mvar。 采用改进的PSO 算法—PSO-w、PSO-cf[10,11]和CLPSO[16]算法与MSI-APSO 算法在2.1GHz,2GB RAM 的intel(R)Core(TM)2PC 机进行仿真测试计算,仿真软件采用matlab7.8.0。 PSO-w 的参数设置:学习因子c1和c2均取为经典值,c1=c2=2,惯性权重w 随迭代次数递减由0.9 线性递减至0.4;PSO-cf 参数设置:学习因子c1和c2均取2.05,压缩因子K = 0.728 3。PSO-cf、PSO-w、CLPSO 算法位置越界时取边界并在1/4 搜索空间取随机量,计算公式见式(23)和式(24),每维最大速度大小为搜索空间的30%;所有算法均对IEEE30 节点系统进行仿真测试。 当粒子位置越下界时,粒子位置为 当粒子位置越上界时,粒子位置为 在本仿真测试中,取算法种群数为30,最大迭代次数为200,潮流计算用牛顿拉夫逊法,每种改进PSO 算法重复运行20 次,得到结果见表4~表7和图1~图2。 表4 基于各种改进PSO 算法的无功优化网损Tab.4 Network active losses of reactive power optimization based on different improved PSO algorithms 图1 基于各种改进PSO 算法的网损收敛曲线Fig.1 Network losses convergence curves based on different improved PSO algorithms 表5 不同改进PSO 算法控制变量优化后的值Tab.5 Values of control variables besed on different improved PSO algorithms 表6 不同改进PSO 算法状态变量(PQ 节点电压)优化后的值Tab.6 Values of state variables(voltage values of PQ nodes)besed on different improved PSO algorithms 表7 不同改进PSO 算法状态变量(各发电机发出无功量)优化后的值Tab.7 Values of state variables(reactive power generated by generators)besed on different improved PSO algorithms 图2 优化后各PQ 节点电压值Fig.2 Each PQ nodes voltage with optimazation 由测试结果可以看出,各种改进PSO 算法采用本文的罚函数法,可严格罚除越界的状态变量,使各个状态变量不越限,这样有利于提高电压质量和维护电气设备,使设备正常有序的运行。本文所提改进PSO 算法对电力系统无功优化取得了较好的效果,使得网损最好值达到了Ploss=17.446 MW,网损率下降16.44%。而且MSI-APSO 算法的收敛迭代次数较其他几种改进PSO 算法少,基本在80代左右就收敛到最优值,收敛精度也较其他几种改进PSO 算法高。当迭代至最大迭代次数时,MSIAPSO 算法所用时间比PSO-cf 稍多,但总体相差不大。从表4 和图1 可知,无论是网损最终值的最好值还是平均值,MSI-APSO 都比其他几种算法更好、收敛速度更快,有功损耗最优值和最差值相差很小,具有很好的收敛性和鲁棒性。 MSI-APSO 是在综合有利于平衡粒子的局部搜索和全局搜索,动态改变惯性权重,提高粒子的收敛速度,保留粒子优良信息几方面对基本PSO算法进行的改进。MSI-APSO 在收敛精度、收敛速度和收敛稳定性方面都具有很大优势,因此对解决电力无功优化等条件限制问题具有重要意义。 [1]许文超,郭伟(Xu Wenchao,Guo Wei).电力系统无功优化的模型及算法综述(Summarize of reactive power optimization model and algorithm in electric power system)[J].电力系统及其自动化学报(Proceedings of the CSUEPSA),2003,15(1):100-104. [2]祝洪博,徐刚刚,海冉冉,等(Zhu Hongbo,Xu Ganggang,Hai Ranran,et al).基于云自适应梯度粒子群算法的无功优化(Reactive power optimization based on cloud adaptive gradient particle swarm optimization)[J].电网技术(Power System Technology),2012,36(3):162-167. [3]邓佑满,张伯明,相年德(Deng Youman,Zhang Boming,Xiang Niande).配电网络电容器实时优化投切的逐次线性整数规划法(A successive linear integer programming methodology for capacitor switching on distribution systems)[J]. 中 国 电 机 工 程 学 报(Proceedings of the CSEE),1995,15(6):375-383. [4]崔挺,孙元章,徐箭,等(Cui Ting,Sun Yuanzhang,Xu Jian,et al).基于改进小生境遗传算法的电力系统无功优化(Reactive power optimization of power system based on improved niche genetic algorithm)[J].电网技术(Power System Technology),2011,31(19):43-50. [5]聂宏展,张冰冰,王新,等(Nie Hongzhan,Zhang Bingbing,Wang Xin,et al).基于改进粒子群优化算法的电力市场下的无功优化(Research on MPSO algorithm based reactive power optimization in electricity market)[J].电网技术(Power System Technology),2007,31(21):85-90. [6]刘世成,张建华,刘宗岐(Liu Shicheng,Zhang Jianhua,Liu Zongqi).并行自适应粒子群算法在电力系统无功优化中的应用(Application of parallel adaptive particle swarm optimization algorithm in reactive power optimization of power system)[J].电网技术(Power System Technology),2012,36(1):108-112. [7]张文,刘玉田(Zhang Wen,Liu Yutian). 自适应粒子群优化算法及其在无功优化中的应用(Adaptive particle swarm optimization and its application in reactive power optimization)[J].电网技术(Power System Technology),2006,30(8):19-24. [8]顾威,李兴源,王渝红,等(Gu Wei,Li Xingyuan,Wang Yuhong,et al).基于改进粒子群算法的次同步阻尼控制器设计(Design of subsynchronous damping controller based on improved particle swarm optimization algorithm)[J].电网技术(Power System Technology),2010,34(8):52-56. [9]吴方劼,张承学,段志远(Wu Fangjie,Zhang Chengxue,Duan Zhiyuan).基于动态多种群粒子群算法的无功优化(Application of modified particle swarm optimization in reactive power optimization)[J].电网技术(Power System Technology),2007,31(24):35-39. [10]刘述奎,陈维荣,李奇,等(Liu Shukui,Chen Weirong,Li Qi,et al).基于随机聚焦粒子群算法的电力系统无功优化(Reactive power optimization in power system based on stochastic focusing particle swarm optimization)[J]. 电网技术(Power System Technology),2008,32(S2):8-11. [11]刘述奎,陈维荣,李奇,等(Liu Shukui,Chen Weirong,Li Qi,et al).基于自适应聚焦粒子群优化算法的电力系统多目标无功优化(Power system multi-objective reactive power optimization based on adaptive focusing particle swarm optimization algorithm)[J]. 电网技术(Power System Technology),2009,33(13):48-53. [12]曾传华,申元霞(Zeng Chuanhua,Shen Yuanxia).新型分阶段粒子群优化算法(A new phased particle swarm optimization algorithm)[J]. 计算机工程与应用(Computer EngineeringandApplications),2008,44(24):81-82,138. [13]韩富春,刘利红,岳永新(Han Fuchun,Liu Lihong,Yue Yongxin).基于改进粒子群算法的电力系统无功优化研究(Research of particle improved swarm algorithm in power system reactive power optimization)[J]. 电气技术(Electrical Engineering),2011(7):6-8,13. [14]Zimmerman R D,Murillo-Sanchez C E,Gan Deqiang.MATPOWER—A MATLAB power system simulation package [EB/OL].http://www. pserc. cornell.edu/matpower,2013. [15]陈功贵,李智欢,孙永发,等(Chen Gonggui,Li Zhihuan,Sun Yongfa,et al). 电力系统无功优化的LRS-PSO 算法(LRS-PSO algorithm for optimal reactive power flow)[J].电力系统及其自动化学报(Proceedings of the CSUEPSA),2008,20(4):92-97. [16]Liang J J,Qin A K,Suganthan P N,et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]. IEEE Trans on Evolutionary Computation,2006,10(3):281-295.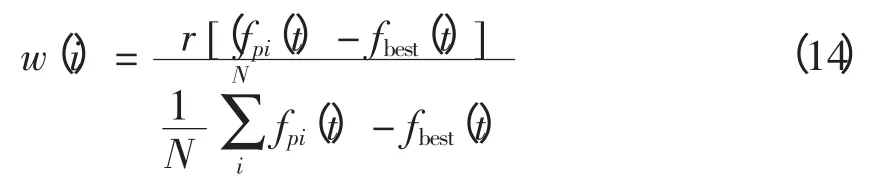
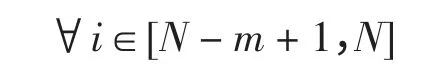
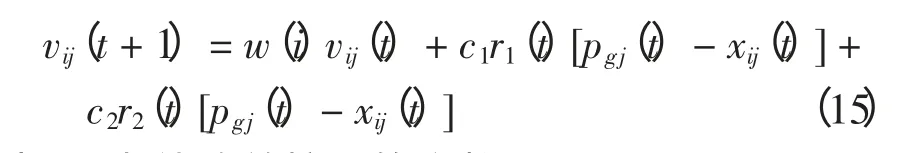
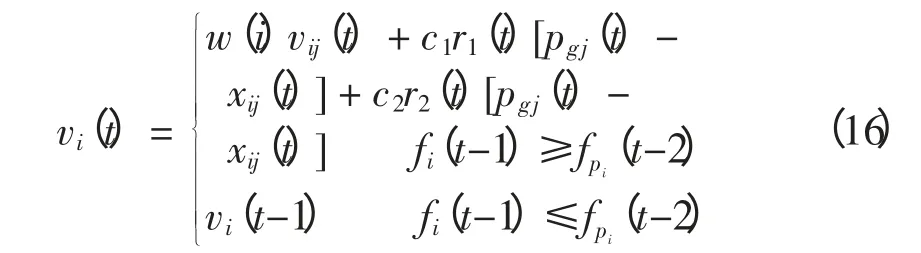
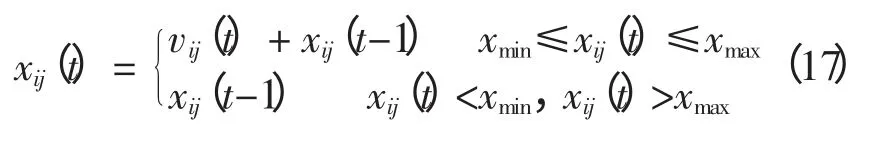
3 基于MSI-APSO 算法的无功优化步骤
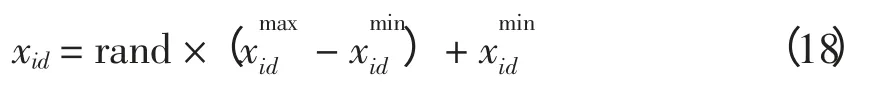

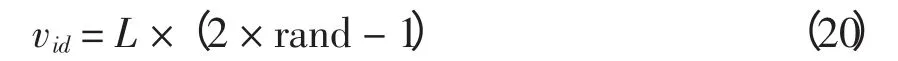
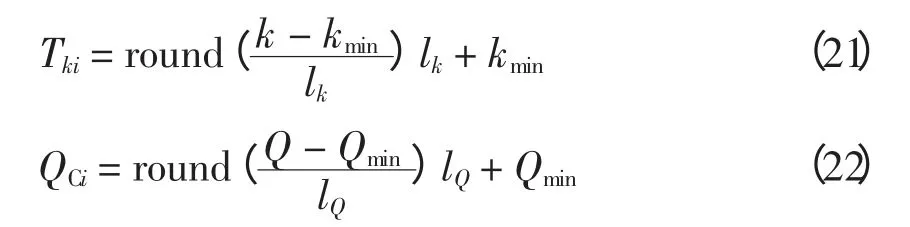
4 算例分析
4.1 仿真环境设置


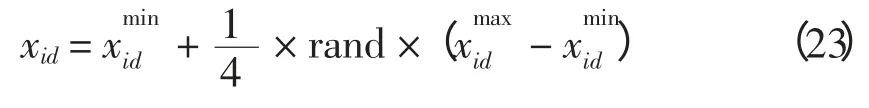
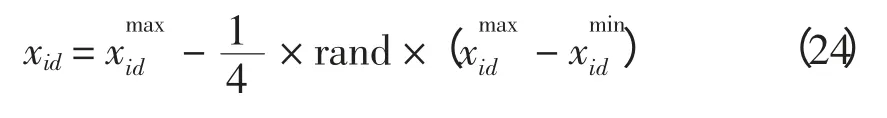
4.2 测试结果

5 结语
