P－n－右析取语言的相关性质

刘 莉

（延安大学数学与计算机科学学院，陕西延安716000）

P－n－右析取语言的相关性质

刘 莉

（延安大学数学与计算机科学学院，陕西延安716000）

主要研究了P－n－右析取语言的一些相关性质，给出了P－n－析取辖的定义，得出了P－n－析取辖是稠密语言等结论。

P－n－右析取语言；稠密语言；P－n－稠密

1 基本概念

设X是非空的字符集（有限或无限），我们称X是字母表，X上的元素称为字母，X上的有限字符串称为X上的字，我们定义空字是不包含任何字母的字，用1表示空字，记X上的所有字的集合为X*，即

其中X0＝1，

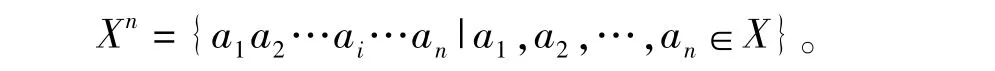
令S是一个非空集合，S×S的子集ρ称为S上的二元关系。若ρ满足下面的条件：

（1）xρx，（∀x∈S）

（2）xρy⇒yρx，（∀x，y∈S）

（3）xρy，yρz⇒xρz，（∀x，y，z∈S）

则称ρ是S上的等价关系。

等价关系ρ称为右同余（左同余），若满足aρb⇒acρbc（aρb⇒caρcb），∀c∈S。

若ρ既是右同余又是左同余，称ρ是同余关系。

设X是一个有限字母表，定义X*上的全序如下：∀x，y∈X*，若lg（x）＜lg（y）。则x＜y；若lg（x）＝lg（y）＝n，∀n≥1，则定义＜是Xn上的字典序，例如，设X＝｛a，b，c｝，则X*＝｛1＜a＜b＜c＜aa＜ab＜ac＜ba＜bb＜…｝。

定义1［1］设L⊆X*，定义X*上的等价关系Pn，L：

其中u，v∈X*，uy≠1，vy≠1。则Pn，L是X*上的右同余关系。

定义2［2］设L⊆X*，称L是P－n－右析取语言：如果Pn，L是X*上的恒等关系。

定义3［3］称L是P－n－稠密的，如果满足：∀u∈X*，∃x，y∈X*，∃n，s.t.x（uy）n∈L。

定义4［3］称L是P－n－离散的，如果满足

引理1［4］若um＝vn，m，n≥1，则u，v是同一字的方幂。

引理2［5］令L⊆X＋，则下列条件等价：

（1）L是P－n－稠密语言；

（2）L（k）是P－n－稠密语言；

引理3［5］一个语言是P－n－稠密的当且仅当它包含有一个P－n－右析取语言。

2 主要结论

定义语言D⊆X*称为P－n－析取辖。如果D满足对任意L⊆X*，若Pn，L在D上是恒等关系，则L是P－n－右析取语言。

命题1设X是有限字母表，D⊆X*，若D是P－n－析取辖，则D是稠密语言。

证明：令X*＝｛u1＜u2＜u3…＜un＜…｝，我们利用P－n－右析取辖D作语言。

L＝｛x′｜x∈D/｛1｝｝，

这里＃x就是x在全序X*中的位置。显然，x与x′是一一对应的。由于lg（x）＜＃x，所以x′是本原字。即L⊆Q。

令L（k）＝｛uk｜u∈L，k∈N｝，

用染色序列对P进行着色,实际上是对m(2n+1)+2n-1条边进行着色,而图4中色集合的个数有个,根据上述染色算法,当k是奇数时,有当k是偶数时,有因此恒成立,此时求得最小的整数k满足⎤。

下证Pn，L（k）是D上的恒等关系。

首先，令x，y∈D/｛1｝，x≠y，不妨设＃x＞＃y，＃x＝n。

（1）若x∉X*a，则存在空字1和an使得

1（xan）k＝（xan）k∈L（k）

假设 1（yan）k＝（yan）k∈L（k），

由L（k）的定义知∃z∈D/｛1｝，＃z＝m使得（yan）k＝（z′）k。

①若z∉X*a，则（yan）k＝（zam）k。

令lg（yan）＝p，lg（zam）＝q，则（yan）q＝（zam）p。

由引理1知yan和zam是同一字的方幂。又yan，zam∈L⊆Q，故yan＝zam。

若lg（y）＜lg（z），则∃z1∈X＋使得z＝yz1，故an＝z1am，但z∉X*a，z1是z的后缀，从而z1∉X*a，即z1不是以a结尾，这与an＝z1am矛盾。

若lg（y）＞lg（z），则y＝zal其中l＋n＝m，l＞0。由y＝zal知＃y＞＃z，又＃x＞＃y，＃x＝n，＃z＝m故有n＞m，这与l＋n＝m矛盾。

②若z∈X*a，则（yan）k＝（zbm）k从而yan＝zbm，但a≠b 故 yan≠zbm矛盾。

因此，假设不成立。故（yan）k∉L（k）。

即x与y没有（Pn，L（k））关系。

（2）若x∈X*a，则类似可以证明存在空字1和bn使得1（xbn）k＝（xbn）k∈L（k）但1（ybn）k＝（ybn）k∉L（k）。从而即x与y没有（Pn，L（k）关系。

其次，对∀x∈D/｛1｝，不妨设x＝x1a，x1∈X*，＃x＝n则存在空字1和bn使得1（xbn）k＝（xbn）k∈L（k），1（1bn）k＝1（1bn）k＝∉L（k）。

从而即x与1没有（Pn，L（k））关系。

综上∀x，y∈D，x≠y，x与y没有（Pn，L（k））关系。

又D是P－n－右析取辖，故L（k）是P－n－右析取语言。

由引理2知L是P－n－稠密语言。

假设D不是稠密语言。则∃w∈X＋，

由于L是P－n－稠密语言，从而∀wk∈X＋，其中w与k的末尾字母互异。∃u，v∈X*，∃n，s.t.u（wkv）n∈L，由L得作法知uwv1∈D，其中v1是kv的前缀，这与X*wX*∩D＝Ø矛盾。

因此D是稠密语言。

命题2设L⊆X*，若L是P－n－右析取语言，则L′＝L∩X*/（X＋）（k），其中k∈N，是P－n－右析取语言。也就是说P－n－右析取语言中所有最终周期字所作的集合还是P－n－右析取语言。

证明：对于∀u，v∈X*，u≠v，由于L是P－n－右析取语言。所以u和v没有Pn，L关系。即∃x，y∈X*，n≥2，有x（uy）n∈L，x（vy）n∉L或x（vy）n∈L，x（uy）n∉L。

不妨设x（uy）n∈L，x（vy）n∉L，

又 L′＝L∩X*（X＋）（k），故

即u和v没有Pn，L′关系。

由u，v的任意性知L′是P－n－右析取语言。

命题3设L1⊆X*是P－n－右析取语言，L2⊆X*/X*（X＋）（k），则L＝L1∪L2是P－n－右析取语言。

证明：对于∀u，v∈X*，u≠v，由于L1是P－n－右析取语言。故u和v没有Pn，L1关系。即∃x，y∈X*，n≥2，有

不妨设x（uy）n∈L1，x（vy）n∉L1，

则x（uy）n∈L，x（vy）n∈X*（X＋）（k），故

即x（vy）n∉L2，x（vy）n∉L。

所以u和v没有Pn，L关系。

由u，v的任意性知L是P－n－右析取语言。

P－n－右析取语言与任一非最终周期字的并还是P－n－右析取语言，也就是说X*中不存在极大的P－n－右析取语言。

命题4设L⊆X*是P－n－右析取语言，若L＝L1∪L2且L1∩L2＝Ø，则下面两式中至少有一个成立：（1）L1和L2中至少有一个是P－n－右析取语言；

（2）L1和L2都包含P－n－右析取语言。

证明：假设（2）不成立，即L1和L2中至少有一个不包含P－n－右析取语言。不妨设L1不包含P－n－右析取语言。由引理3可知，L1不是P－n－稠密语言。则∃w∈X*，∀x，y∈X*，∀n∈N 有x（wy）n∉L1，（*）。

下证∀u，v∈X*，若u≡v（Pn，L2），则u＝v。

事实上，由同余关系的性质有

O159

A

1004－602X（2014）03－0024－03

10.13876/J.cnki.ydnse.2014.03.024

2014-06-20

刘 莉（1985—），女，陕西延安人，延安大学助教。