Smarandache函数在数列ap-bp上的一个下界估计
2014-02-28郝虹斐鲁伟阳
高 丽,郝虹斐,2,鲁伟阳
(1.延安大学数学与计算机科学学院,陕西延安716000;
2.榆林市清涧县店则沟镇九年制学校,陕西榆林719000)
Smarandache函数在数列ap-bp上的一个下界估计
高 丽1,郝虹斐1,2,鲁伟阳1
(1.延安大学数学与计算机科学学院,陕西延安716000;
2.榆林市清涧县店则沟镇九年制学校,陕西榆林719000)
研究Smarandache函数在数列ap-bp上的下界估计问题。利用初等方法和组合方法,证明了估计式S(ap-bp)≥10 p+1,其中p≥17为任意素数,a与b为任意不同的正整数,且a>b。结论给出了Smarandache函数在数列ap-bp上的一个较强的下界估计。
Smarandache函数;下界估计;初等方法;组合方法
对于任意的正整数n,F.Smarandache给出Smarandache函数S(n)被定义为最小的正整数m,使得n|m!,即S(n)=min{m:m∈N+,n|m!}。其中N+表示所有的正整数集合。假设n的标准分解式为:n,依据S(n)的定义易得:S(n)=,由此容易通过计算可以得到:S(1)=1,S(2)=2,S(3)=3,S(4)=4,S(5)=5,S(6)=3,S(7)=7,S(8)=4,…。而关于函数S(n)的初等性质,近几年有许多学者进行了研究,并获得了不少有趣的结论[1-4]。例如陆亚明[1]研究了关于Smarandache函数S(n)的方程,并证明了

的可解性问题,并利用解析数论中的三素数定理证明了对于任意正整数k≥3,该方程有无数组正整数解(m1,m2,m3,…,mk)。
此外,一些学者对Smarandache函数S(n)在某特殊数列上的下界估计做出研究。其中,苏娟丽[2]研究了S(2p+1)的下界估计问题,证明了:当p≥17且为素数时,有估计式

温田丁在文献[3]中更精确了文献[2]的结果,证明了:当p≥17为素数时,有估计式

文献[4]中石鹏等人则讨论了S(n)在特殊数列ap+bp上的下界估计问题,证明了:当a与b为任意不同的正整数,p≥17为素数时,有估计式

受到文献[2-4]的启示,本文利用初等方法及组合方法,研究Smarandache函数S(n)在特殊数列ap-bp上的下界估计问题,并获得了一个较强的估计式。从而得到结果为:
定理设p≥17为素数,a与b为任意不同的正整数,且a>b,有估计式

1 相关引理
引理1 设p为奇素数,对于任意互素的正整数a及b,且a>b,有



由于(a,b)=1,d|a-b,所以(a,b)=1,进而由(1)式立刻推出d|p,进而推出d=1,p。
引理2[5]对任意素数p,正整数及α,t及n,有

则S(pα)≥S(pt)≥pt。
2 定理的证明
本节利用初等方法和组合方法给出定理证明。
由引理2中Smarandache函数S(n)的性质知:对任意素数p,若p|n,有S(n)≥S(p),而且p|S(pα)对任意满足α≤p的正整数α成立。所以对任意素数p≥17,令q为ap-bp的任意素因子,显然q≥3,于是可得S(ap-bp)≥q,又因为q|ap-bp,因而ap-bp≡0(mod q),或者

因此p是(a,b)p模q的指标,则由上式及指标的性质[6-7]知

由于q为奇素数,那么m一定是偶数,因而可以设

于是由式(2)知ap-bp有以下5种可能:
1.ap-bp为p的方幂。假设ap-bp=pα,当α=2时,有ap-bp≥2p-1≥p2,所以α≥3。由引理1不难推出a-b=pk·μ,其中k∈N+,(p,μ)=1。因为a-b|ap-bp,从而μ=1。当时,有k=0,或k=α,即a-b=1或a-b=pα,此时有

2.除p以外,ap-bp至少含有4个素因子。由(3)式知,至少存在一个素因子q,使得q=2kp+1,k≥4,因为当素数p≥5时,2p+1和4p+1不可能同时为素数,此时

3.除p以外,ap-bp仅含有3个素因子q1,q2,q3。由(3)式可设q1=2k1p+1,q2=2k2p+1,及q3=2k3p+1,而当p≥17时,2p+1和4p+1不可能同时为素数,则至少存在一个素因子,不妨设为q3,此时q3=2k3p+1≥8p+1,k3≥4,则一定有S(ap-bp)≥q3=2k3p+1≥8p+1。
4.ap-bp除p以外,仅含有2个素因子。由(3)式知,ap-bp不可能同时包含素因子2p+1和4p+1,因而由(3)式及S(n)的性质,可以分为以下形式:

若ap-bp=pα(2p+1)β(6p+1)γ成立,当β≥4或γ≥2时,由引理2知

或者

当1≤β≤3或γ=1,现在证明在这种情况下,当p≥17时,ap-bp不可能含有p的方幂,若不然,当α≥2时,由Euler-Fermat定理知:

令a-b=pk·μ,(p,μ)=1,由引理1可得k=α或者k=α-1,显然ap-bp=pα(2p+1)β(6p+1)且1≤β≤3,k=α不可能。因为此时

矛盾。于是可设k=α-1,同样的的方法可以推出矛盾。
当α=1时,由于a-b≡ap-bp≡0(mod p),可以得到k=α=1,此时有p2整除ap-bp显然这是不成立的。因而ap-bp不含素因子p。这样可得到

其中1≤β≤3,且p≥17为素数,通过计算得出上式不成立。
同理可证当ap-bp=pα(2p+1)β(6p+1)γ与ap-bp=pα(4p+1)β(6p+1)γ,素数p≥17时,结论S(ap-bp)≥8p+1成立。
5.ap-bp除p以外,仅含有1个素因子。因而由(3)式及S(n)的性质,可以考虑以下三种形式:

若ap-bp=pα(2p+1)β成立,当β≥4时,由引理2有

当β≤3时,由情况4可知ap-bp不含素因子p的方幂,故当α≥1时,ap-bp=pα(2p+1)β且1≤β≤3不成立,故ap-bp=(2p+1)β。当β=3,ap-bp=(2p+1)3时,有
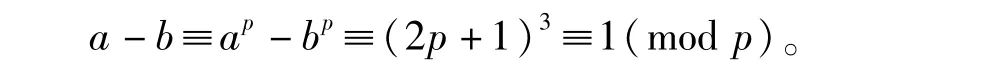
而a-b|ap-bp,所以可设a-b=(2p+1)n,由引理1可知

所以 n=0,3。
即a-b=1或a-b=(2p+1)3=ap-bp,这与(a,b)=1且a≥b+1,p≥17以及a-b<ap-bp矛盾。显然2p-1≤ap-bp=(2p+1)β,由1≤β≤2与p≥17。通过计算可得上述不等式不成立。
同理可证:ap-bp=pα(4p+1)β或ap-bp=pα(6p+1)β时定理成立,于是定理得证。
[1]Lu Yaming.On the soulution of an equation involving the Smarandache function[J].Scientia Magna,2006,2(1):76-79.
[2]苏娟丽.关于Smarandache函数的一个下界估计[J].纺织高校基础科学学报,2009,22(1):133-134.
[3]温田丁.Smarandache函数的一个下界估计[J].纯粹数学与应用数学2010,26(3):413-416.
[4]石鹏,刘卓.Smarandache函数在数列上的一个下界估计[J].西南师范大学学报(自然科学版),2013,38(8):10-14.
[5]Mark F,Patrick M.Bounding the Smarandache Function[J].Smarandache Notion Journal,2002,13(1):2-3.
[6]张文鹏.初等数论[M].西安:陕西师范大学出版社,2007.
[7]Apostol TM.Introduction to Analytic Number Theory[M].New York:Spring-VErlag,1976.
[责任编辑 毕 伟]
A Lower Bound Estimate for Smarandache Function on Sequence ap-bp
GAO LI1,HAO Hong-fei1,2,LUWei-yang1
(1.College of Mathematics and Computer Science,Yanan University,Yanan 716000,China;
2.Dianzegou Nine-year School,Yulin 719000,China)
To study a lower bound estimate problem of Smarandache Function on Sequence ap-bp.Using the elementary and combinationalmethods.It is proved the Estimate S(ap-bp)≥8p+1,where p≥17 be any prime,a and b are two positive integers with a>b.A lower bound estimate of Smarandache Function on Sequence ap-bpis given.
Smarandache function;lower bound estimate;elementarymethod;combinationalmethod
O156.4
A
1004-602X(2014)03-0001-03
10.13876/J.cnki.ydnse.2014.03.001
2014 05 06
国家自然科学基金资助项目(10271093);延安大学自然科学专项科研基金项目(YDZ2013-04);延安大学硕士研究生教育创新计划项目
高 丽(1966—),女,陕西绥德人,延安大学教授。
