粘性Cahn－Hilliard方程全局吸引子的维数估计

董超雨，姜金平，张晓明

（延安大学数学与计算机科学学院，陕西延安716000）

粘性Cahn－Hilliard方程全局吸引子的维数估计

董超雨，姜金平，张晓明

（延安大学数学与计算机科学学院，陕西延安716000）

借助不等式的技巧，得到粘性Cahn－Hilliard方程在L2（Ω）空间中全局吸引子的维数估计。

粘性Cahn－Hilliard方程；全局吸引子；维数

1 引言及预备知识

考虑下列粘性Cahn－Hilliard方程：

粘性系数δ＞0，当δ＝0时，方程（1）是Cahn－Hilliard方程。Ω是Rn（n≤3）中的有界集，f（u）是首项系数为正的奇次多项式：

令H＝L2（Ω），V＝（Ω）。C，c，c1，c2，…表示依赖于Ω与m常数。齐次边界条件下，对称算子A＝－△，且A具有有界逆A－1。

定义1半群S（t）在全局吸引子A上是一致可微的，如果对∀u∈A，存在线性算子L（t，u），使得对所有的t≥0，有

定义2（L（s，u0）Qm（τ））d]s，Qm是投影算子。

定理1［1］设u0∈H，初值问题（1）－（3）在H中存在全局吸引子A＝ω（B），且A在H的范数下吸引H中的一切有界集。

2 全局吸引子的维数估计

令A*＝A－1＋δI，方程（1）－（3）的线性化方程

定理2［2］设半群S（t）在全局吸引子A上是一致可微的且存在时间t0，使得L（t；u0）对所有的t≥t0是紧的。如果TRM（A）＜0，则df（A）≤M。

定理3初值问题（1）－（3）产生的半群S（t）在全局吸引子A上一致可微的，并且对∀t≥0，L（t，u0）是紧算子。

证：设u（t），v（t）是问题（1）－（3）的解，u0，v0∈A，U（t）是初值问题（6）－（7）的解，U（x，0）＝u0－v0。令w（t）＝u（t）－v（t）－U（t），则

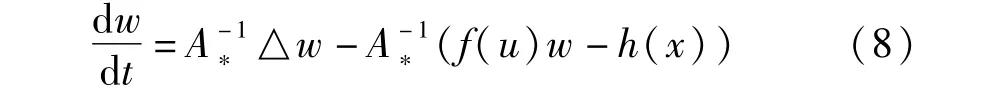
其中h（x）＝f（v）－f（u）－f′（u）（v－u），则｜h（x）｜≤｜f″（v＋θ（u－v））‖u（x）－v（x）｜2，其中0≤θ≤1，由文献［3］知A在L∞中有界，所以

｜h（x）｜≤C｜u（x）－v（x）｜2。

由标准方法得｜u－v｜≤ect｜u0－v0｜，则

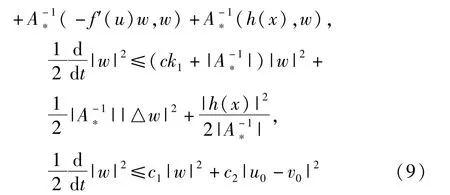
由Gronwall不等式得｜w｜2≤c3｜u0－v0｜2。所以S（t）一致可微。

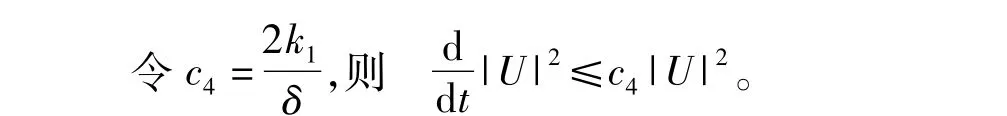
由Gronwall不等式得｜U（t）｜2≤e2c4t｜Ψ｜2，即

｜L（t，u0）Ψ｜2≤e2c4tΨ｜2。

故L2（Ω）中的有界集在L（t，u0）作用下是有界集，则‖L（t，u）‖op＜∞，∀t≥0。所以S（t）在全局吸引子A上一致可微。

由Gronwall不等式可得‖U‖2是有界，L（t， u0）把H＝L2（Ω）中的有界集映成V＝（Ω）中的有界集，所以L（t，u0）是紧算子。

定理4初值问题（1）－（3）在H中全局吸引子的维数是有限的，维数估计其中常数k2只与m及Ω的形状有关，与Ω，m及φj无关。

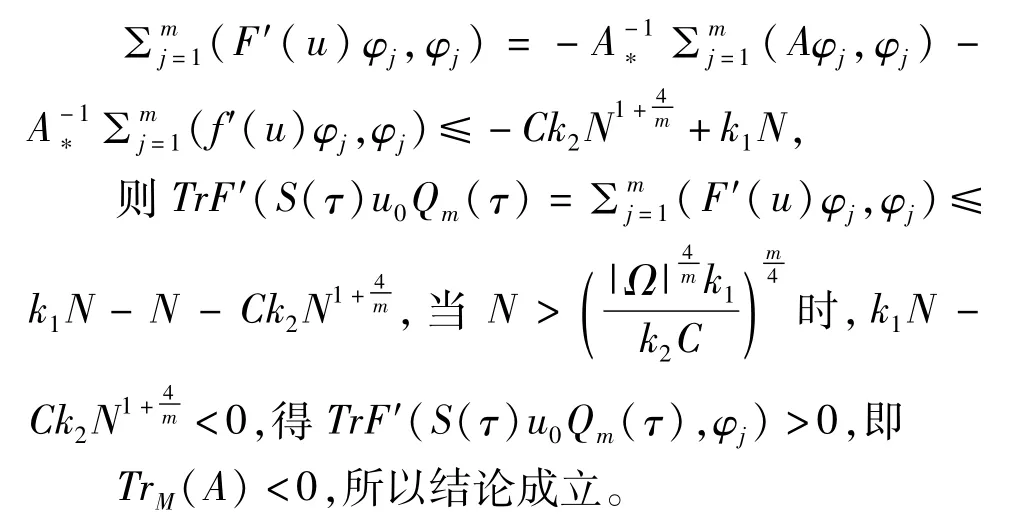
［1］董超雨，姜金平等.粘性Cahn－Hilliard方程在L2空间中的全局吸引子［J］，贵州大学学报（自然科学版），2013，30（4）：7－9.

［2］Robinson JC.Infinite－dimensional dynamical systems：an introduction to dissipative parabolic PDEs and the theory of global attractors［M］.Cambridge Uni.Press，2001.

［3］董超雨，姜金平，等.粘性Cahn－Hilliard方程全局吸引子的存在性［J］.湖北大学学报（自然科学版），2014，36（4）：385－388.

［4］Teman R.Infinite dimensional Dynamical Systems in Mechanics and Physics［M］.New York：Springer，1997.

［责任编辑 毕 伟］

Dimension Estimation for the G lobal Attractor of the Viscous Cahn－Hilliard Equation

DONG Chao-yu，JIANG Jin-ping，ZHANG Xiao-ming
（College of Mathematics and Computer Science，Yanan University，Yanan 716000，China）

Using inequality technique，the estimation of dimension for the global attractor of the viscous Cahn－Hilliard equation in the space L2（Ω）was got.

viscous Cahn－Hilliard equation；global attractor；dimension

O175.29

A

1004－602X（2014）03－0015－02

10.13876/J.cnki.ydnse.2014.03.015

2014-08-29

董超雨（1988—），男，陕西吴堡人，延安大学在读硕士研究生。