等比数列构成的一类特殊Hankel矩阵的逆矩阵

周 勇，刘兴祥，张 莉

（1.清涧县解家沟镇九年制学校，陕西榆林719000；

2.延安大学数学与计算机科学学院，陕西延安716000）

等比数列构成的一类特殊Hankel矩阵的逆矩阵

周 勇1，刘兴祥2，张 莉2

（1.清涧县解家沟镇九年制学校，陕西榆林719000；

2.延安大学数学与计算机科学学院，陕西延安716000）

给出了由等比数列构成的一类特殊Hankel矩阵的逆矩阵存在的条件及其公式解。

Hankel矩阵；逆矩阵；等比数列

Hankel矩阵是一类非常重要的特殊矩阵，其经常出现在随机过程、时序分析、数字滤波、幂距量等应用领域。对Hankel的性质和应用的探讨过程是矩阵理论中的一个非常重要的课题，文献［1－4］分别证明了Hankel矩阵如果可逆，其逆矩阵也为Hankel矩阵，并给出了求逆矩阵的方法。文献［5］则讨论了由等差数列构成的一类特殊Hankel矩阵。本文是在以上文献的基础之上，讨论了由等比数列构成的一类特殊Hankel矩阵，并给出了其逆矩阵存在的条件和公式解。

1 预备知识

定义1具有形状

的矩阵H∈Mn（F）称为Hankel矩阵。

性质1定义的矩阵H，是由H的第1行和第n列的2n－1个元素a1，a2，…，an，an＋1，…，a2n－1所唯一确定。

定义2一般地，如果一个数列从第二项起，每一项与前一项的比等于同一个非零常数，这个数列就称为等比数列。这个常数叫做等比数列的公比，通常用q表示。an＝a1qn－1，（a1≠0）称为等比数列｛an｝的通项公式。

定理1若构成Hankel矩阵H的2n－1个元素a1，a2，…，an，an＋1，…，a2n－1构成等比数列，那么H不可逆。

证明设ak＝a1qk－1（a1≠0且k＝1，2，…，2n－1），则

显然，r（H）＝1＜n，所以H不可逆。

引理1 在H中，令an＋1＝a1，an＋2＝a2，…，a2n－1＝an－1，则可得到

为H的一种特殊情况。此时，特殊Hankel矩阵H0是由第1行的n个元素a1，a2，…，an确定。

引理2［4］若上述H0为n阶实Hankel矩阵（即H0∈Mn（R）），如果H0可逆，则H－10也为n阶实Hankel矩阵，且与H0同型。记

2 主要结论

定理2 若构成特殊Hankel矩阵H0的n个元素a1，a2，…，an成等比数列，即ai＝a1qi－1（i＝1，2，…，n），且a1≠0，q≠1（当q＝1时H0是不可逆的）。则当∑n

i＝1ai≠0时，特殊Hankel矩阵H0的逆矩阵存在，且其逆矩阵形如H0－1是由b1，b2，…，bn生成。

证明分析可知，只需求出bi（i＝1，2，…，n）即可。由可知＝E，由乘的第一列等于E的第一列，得bi（i＝1，2，…，n）满足也就是说构造了关于未知量bi（i＝1，2，…，n）的非齐次线性方程组，只需要解出bi（i＝1，2，…，n）即可。注意到ai＝a1qi－1（i＝1，2，…，n），且a1≠0，q≠1，当≠0时，对其增广矩阵进行矩阵的初等变换：

不难得到公式解：

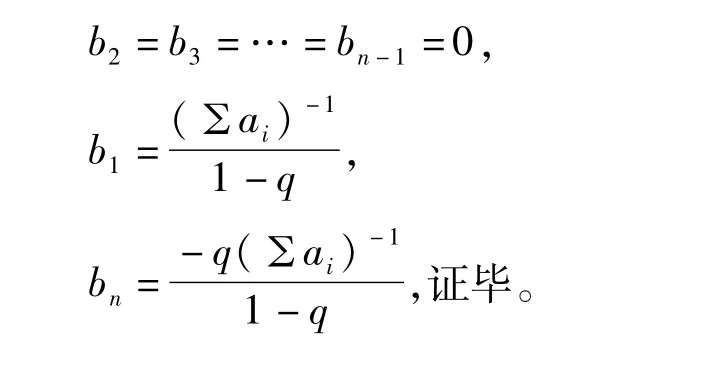
3 数值例子

解 不难发现，矩阵A是一个由等比数列构成的特殊Hankel矩阵，公比q＝2，n＝4，∑ai＝15≠0，由上述定理2知，矩阵A可逆，且可设

由定理2给出的公式解可得：

通过A－1A＝AA－1＝E验证是容易的。

4 小结

本文是在文献［1］到文献［5］的基础之上，讨论了由等比数列（一等比数列）构成的一类特殊Hankel矩阵，并给出了其逆矩阵存在的条件和公式解。后续将对双等比、双等差、等差等比、等比等差等情况作进一步的研究论证。

［1］Joseph A Silva.A theorem on Cyclic Matrices［J］.Duke Mathematical Journal，1951，18（4）：821－825.

［2］Chao Chongyun.On a type of Circulant［J］.Duke Mathematical Journal，1973，40（6）：241－248.

［3］陈景良，陈向晖.特殊矩阵［M］.北京：清华大学出版社，2001.

［4］毛纲源.实（－1）—循环矩阵的性质［J］.武汉工业大学学报，1994，16（1）：122－126.

［5］卢诚波.等差序列构成的矩阵的逆矩阵［J］.丽水学院学报，2006，28（2）：5－7.

［责任编辑 毕 伟］

The Inverse M atrices of A Special Hankel M atrices M ade of Geometric Progression

ZHOU YONG1，LIU Xing-xiang2，ZHANG LI2
（1.Hai Jiagou Nine－Year Compulsory Education School，Yulin 719000，China；
2.College of Mathematics and Computer Science，Yanan University，Yanan 716000，China）

A formula solution of the inversematrices of a special Hankelmatricesmade of geometric progression is given.

Hankelmatrix；inversematrix；geometric progression

O151.21

A

1004－602X（2014）03－0021－03

10.13876/J.cnki.ydnse.2014.03.021

2014-06-13

周 勇（1990—），男，陕西甘泉人，清涧县解家沟镇九年制学校教师。