基于CFDSE的RFID标签数动态估算方法

蔡晓思,刘桂雄,吴国光

（华南理工大学机械与汽车工程学院，广东 广州 510640）

基于CFDSE的RFID标签数动态估算方法

蔡晓思,刘桂雄,吴国光

（华南理工大学机械与汽车工程学院，广东 广州 510640）

针对切比雪夫不等式标签数估算方法运算量较大的问题，提出粗精二次搜索RFID标签数动态估算方法（CFDSE），基于由粗至精搜索思想，第一次搜索用加减运算消除平方、开方运算，同时减少第二次搜索范围，可使第二次搜索范围减少约90%。第二次搜索采用切比雪夫不等式估算方法，提高估算准确度。仿真实验表明：CFDSE估算误差小于5%，估算时间比切比雪夫不等式法减少约54%。

RFID技术；标签数估算；粗精二次搜索；切比雪夫不等式

0 引 言

RFID是物联网关键技术之一，在工业自动化、物流管理、定位等领域有广阔的应用潜力[1-3]。多标签碰撞是影响RFID信息快速获取的主要问题之一，为有效降低碰撞概率，需根据标签数设置读写器参数，但通常识别区域标签数未知，故首先准确估算标签数，有助于提高标签防碰撞算法效率。目前RFID标签数估算方法主要有：（1）基于碰撞最小值、泊松分布、空闲时隙数估算法等条件假设，建立标签数与时隙统计量解析式，估算标签数，但该方法关系式固定，估算误差随标签数增加迅速增大，不适用于标签数较多场合[4-6]；（2）利用空闲、可读、碰撞时隙数统计信息，在标签数搜索区间，寻找使评定指标满足最小或最大条件的标签数，如基于切比雪夫不等式、最大似然、贝叶斯估计等估算法等[7-9]。基于区间搜索的标签数估算方法准确度较高，是标签数估算的发展方向，但算法复杂、计算量大，不适用于计算能力较差的嵌入式读写系统开发。若能在保证准确度前提下，降低算法运算量，则该方法将更具应用价值。

本文在切比雪夫不等式估算方法基础上，提出一种粗精二次搜索（coarse-fine double searching-based tag estimation method，CFDSE）的标签数动态估算方法，在准确性、复杂度等性能指标有显著改进。

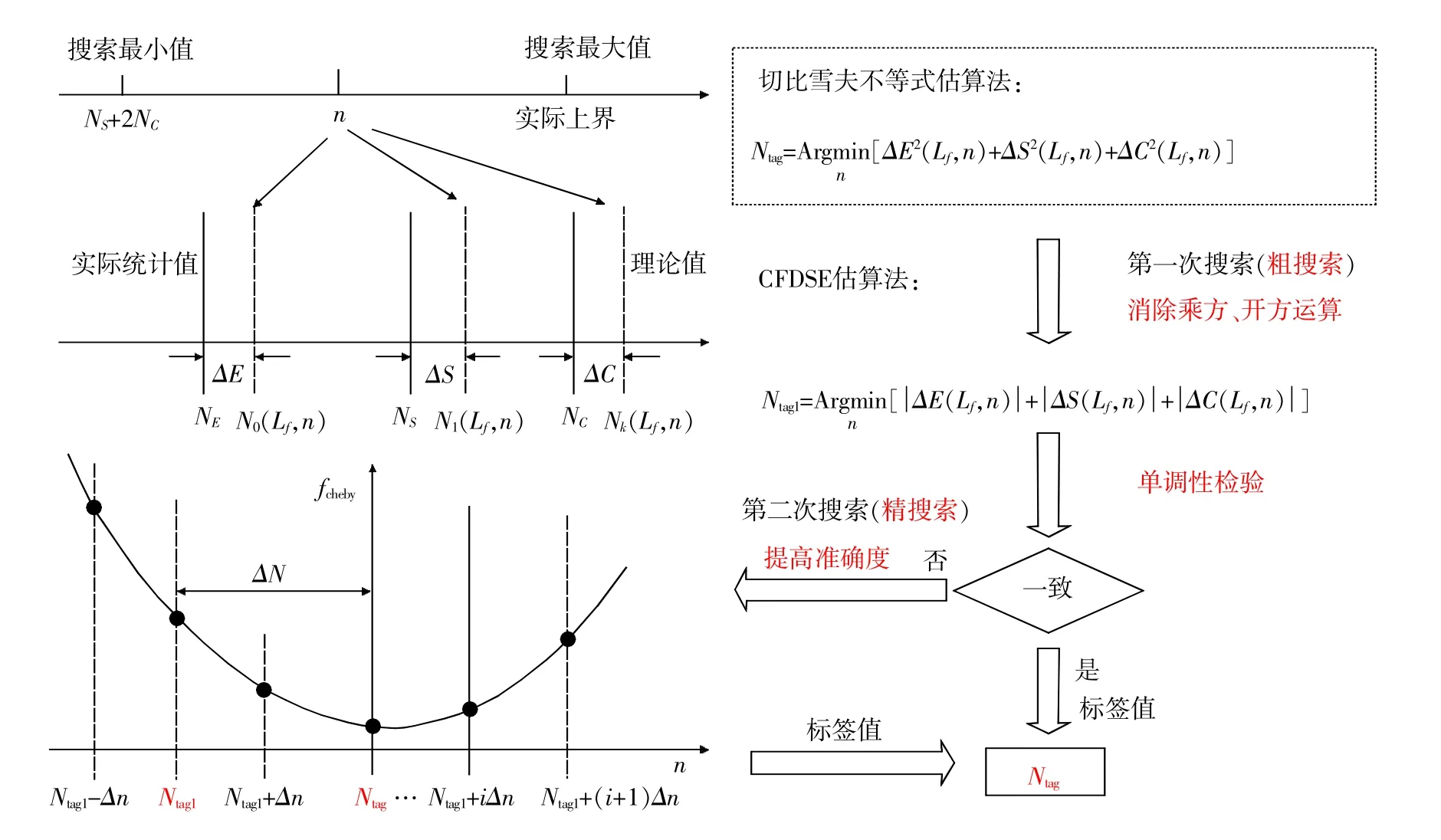
图1 CFDSE标签数估算方法与切比雪夫不等式估算法实现原理对比示意图

1 CFDSE标签数估算方法原理架构

图1为基于CFDSE标签数估算法与切比雪夫不等式估算法的实现原理对比示意图。

粗精二次搜索标签数动态估算方法首先以空闲、可读、碰撞时隙数统计量与理论期望值的绝对值距离函数fCFDSE（）=|ΔE|+|ΔS|+|ΔC|为指标，在标签数取值区间，搜索使该函数取得最小值的标签数为第一次搜索结果，实现粗搜索。若fCFDSE（）与切比雪夫不等式函数fcheby（）=ΔE2（Lf，n）+ΔS2（Lf，n）+ΔC2（Lf，n）单调性相同，则Ntag=Ntag1，这样就实现以另外一种评价指标代替，用加减运算代替平方、开方运算；若fCFDSE（）与fcheby（）单调性不同，再以Ntag1为中心搜索，用切比雪夫不等式估算法进行第二次精搜索，在Ntag1附近将得到Ntag，由于搜索区间减小，整个搜索范围平方、开方运算减少，运算量也可减小。

2 标签数估算方法工作流程

图2为基于CFDSE标签数估算方法流程图。具体包括：确定标签数搜索范围[Nmin～Nmax]；计算NE、NS、NC与理论期望值的绝对值距离fCFDSE（）；CFDSE方法求第一次标签估计值Ntag1；Ntag1单调性检验判断；采用切比雪夫不等式估算法进行二次搜索求Ntag等，下面简单对算法进行说明。

（1）确定标签数搜索范围[Nmin～Nmax]。Nmin基于碰撞时隙至少有两个标签应答条件有Nmin=NS+2NC，Nmax为实际应用场合最大标签数。

图2 基于CFDSE标签数动态估算方法流程图

（2）计算NE、NS、NC与理论期望值的绝对值距离fCFDSE（）。若空闲、可读、碰撞时隙数的理论期望值分别为

可得CFDSE法搜索的绝对值距离公式为

（3）CFDSE方法求第一次标签估计值。在搜索范围[Nmin～Nmax]内，搜索使fCFDSE（）取得最小值的标签数则为第一次标签估计值Ntag1，即：

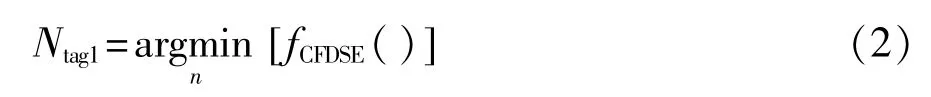
（4）判断Ntag1是否满足单调性检验。通常Ntag1≠Ntag，必须进行单调性检验，保持估算准确性。

若切比雪夫不等式估算法空闲、可读、碰撞时隙数统计量与对应理论期望值平方距离函数为

则切比雪夫不等式估算法标签数Ntag估算式为

由于fcheby[N0（Lf，n），N1（Lf，n），Nk（Lf，n）]≥0，故由函数单调性得标签数估算式：

下面将空闲、可读、碰撞时隙数统计量与对应理论期望值大小关系，讨论函数单调性检验。

1）N0（Lf，n）＞NE、N1（Lf，n）＞NS、Nk（Lf，n）＞NC，则ΔE（Lf，n）、ΔS（Lf，n）、ΔC（Lf，n）均大于 0，fCFDSE（）与fcheby（）同为单调增函数，故 ΔN=0，标签数估计值Ntag=Ntag1；2）N0（Lf，n）＜NE、N1（Lf，n）＜NS、Nk（Lf，n）＜NC，fCFDSE（）与fcheby（）同为单调减函数，Ntag=Ntag1；3）|NE-NS|=|NC-NS|=0，在定义域内单调性一致，标签数估计值Ntag=Ntag1；4）若上述条件不满足，则ΔN≠0，为获得更高估算准确度，以Ntag1为中心，采用切比雪夫不等式估算法进行二次搜索。

（5）采用切比雪夫不等式估算法进行二次搜索。由图 1可以看出，fcheby[N0（Lf，n），N1（Lf，n），Nk（Lf，n）]为凹函数，Ntag为使该函数取得最小值的标签值。二次搜索可看作是以Ntag1为中心搜索该凹函数最小值过程。设第二次搜索步进为Δn，若Ntag1＜Ntag，则搜索终止条件为：fcheby[N0（Lf，Ntag1+iΔn），N1（Lf，Ntag1+iΔn），Nk（Lf，Ntag1+iΔn）]≤fcheby[N0（Lf，Ntag1+iΔn+Δn），N1（Lf，Ntag1+iΔn+Δn），Nk（Lf，Ntag1+iΔn+Δn）]，此时标签数估算值Ntag=Ntag1+iΔn；若Ntag1≥Ntag，则搜索终止条件相反。

3 仿真实验与分析

RFID标签数估算方法必须在保证算法准确性前提下，具有较小运算量，且算法还必须能较快适应标签数变化。下面在Matlab软件平台，对基于CFDSE标签数估算方法进行性能仿真。

标签数估算方法准确性采用估算误差为指标。若Nˆtag为估算标签数，Ntag为实际标签数，则估算误差ε定义为

Ntag[50，1 000]，同一标签数量情况下，各种算法均进行1000次独立实验。图3为5种算法标签数估计值与估算误差曲线图。

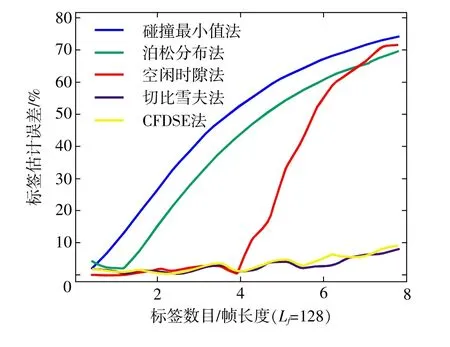
图3 标签数估算方法估算误差图

由图3可以看出：

（1）Ntag/Lf＜5，此情况在实际中较为常见，CFDSE标签数估算法第一次搜索结果与切比雪夫不等式法准确度性能接近，误差随标签数增加不明显且小于5%，优于碰撞最小值估算法、泊松分布法与空闲时隙法。

（2）5≤Ntag/Lf≤8时，CFDSE估算法第一次搜索结果误差小于9%，切比雪夫不等式法估算结果误差小于7%，但CFDSE估算法第一次搜索算法无须平方运算，复杂度较低。

（3）Ntag/Lf＞8时，由于误差增大，需在第一次搜索基础上，结合切比雪夫不等式法进行二次搜索，保证估算方法准确度。

表1为CFDSE标签数估算方法与切比雪夫不等式估算方法复杂度分析比较表。

表1 标签数估算法与切比雪夫不等式估算法复杂度分析比较表

由于CFDSE第一次搜索将3（Nmax-NS-2NC+1）个乘法运算转化为绝对值加减运算，且一般可使第二次搜索范围减少约90%，故CFDSE估算法乘法个数小于0.3（Nmax-NS-2NC+1），运算量显著降低。若乘法、加法、绝对值加减运算时间分别为tmul、tadd、tabs， 令Nsearch=Nmax-NS-2NC+1，则切比雪夫不等估算法、CFDSE法估算时间Tcheby、TCFDSE分别为

Dynamic estimation method for RFID tag based on CFDSE

CAI Xiao-si，LIU Gui-xiong，WU Guo-guang
（School of Mechanical and Automotive Engineering，South China University of Technology，Guangzhou 510640，China）

According to the large computation of Chebyshev inequality-based tag estimation method，the dynamic coarse-fine double searching-based tag estimation method （CFDSE）was proposed.Based on the idea of coarse-to-fine search，the first search eliminates square，square root with addition and subtraction，while reducing the second search range.The second search range can be reduced by about 90%.The second search estimation method using Chebyshev inequality to improve the estimation accuracy.Simulation results show that the CFDSE estimation error is less than 5%，the estimation time of about 54% less than the Chebyshev inequality method.

RFID；tag estimation；CFDSE；Chebyshev inequality

TP391.45；TP391.9；TP18；O242

：A

：1674-5124（2014)03-0098-03

10.11857/j.issn.1674-5124.2014.03.026

2013-06-13；

：2013-07-30

广东省高等学校高层次人才项目（粤教师函[2010]79号文）

蔡晓思（1989-），女，广东揭阳市人，硕士研究生，专业方向为RFID技术、智能传感及仿真建模。