基于曲线拟合的水声换能器转移阻抗测量
2014-10-25冯飞,杨博
冯 飞,杨 博
(1.91388部队,广东 湛江 524022;2.东南大学,江苏 南京 210096)
0 引 言
水声换能器是水下各种发射、接收测量用传感器的总称,它将水下的声信号转换成电信号(接收换能器即水听器),或将电信号转换成水下的声信号(发射换能器)。换能器是声纳的重要组成部分,在水声工程起着关键作用,许多发达国家都投入巨大的力量进行研究[1]。水声换能器必须定期进行校准以保证其可靠性。采用基于虚拟仪器技术的换能器自动校准系统可以在节约人力资源的同时提高校准效率。
对水声换能器的校准来说,可归为如何准确测量换能器-水听器的转移阻抗[2]。传统上,对其测量多采用谱分析法。针对谱分析法存在频谱泄漏及栅栏效应,以及存在多种限制条件的问题,本文提出一种基于Levenberg-Marquardt(L-M)算法的曲线拟合法,实现对传统方法的改进。
1 校准原理
水声换能器的主要性能参数有自由场(电压)灵敏度、发送电流响应、发送电压响应、指向性函数等。根据国家标准[3],自由场灵敏度通常可采用球面波自由场互易法、柱面波自由场互易法、球面波自由场比较法、柱面波自由场比较法、噪声均匀场比较法等。发送响应通常采取比较法测量。
1.1 互易法校准
互易法校准是根据互易换能器遵守的电声互易原理进行校准的一种绝对校准方法[4]。该法采用3个换能器,其中至少有一个互易换能器(H),另两个是发射器(F)和水听器(J)。在自由场远场中按图1所示组合,做3次测量,分别测量每换能器对输入发射器的电流i和水听器的开路电压u或其电转移阻抗,就能获得水听器J和互易换能器H的自由场灵敏度。计算公式为式(1)、式(2)。

图1 互易法校准

式中:MfJ,MfH——水听器J和互易换能器H在频率f下的自由场灵敏度;
dXY——两换能器的声中心之间的距离;
ZXY——每队换能器间的转移阻抗,定义为接收端开路电压和发送端发送电流的比值。
1.2 比较法校准
比较法校准是与标准水听器或标准声源比较的一种相对校准方法[3]:将发射器(F)、标准水听器(P)及待校水听器(X)按图2所示排列,分别测量换能器对(F-P)、(F-X)的电转移阻抗模|ZFP|和|ZFX|,则待校水听器的自由场灵敏度MX为
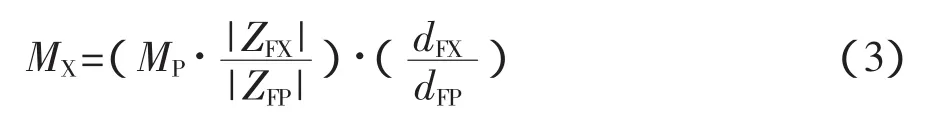
从换能器各项主要参数的获得方法[3]可以看出,校准换能器的关键是获得换能器的转移阻抗ZXY,即水听器的开路电压与发射换能器的输入电流之间的复数比值。
2 基于谱分析法的转移阻抗测量
基于谱分析法的转移阻抗测量主要采用以下3种方法[5]:(1)谱分析法。该方法首先对采样信号做傅里叶变换,然后以离散傅里叶变换(DFT)进行计算即可得到信号幅值。(2)加窗谱分析法。该方法对信号直接进行截断以进行DFT的计算,相当于对给信号加矩形窗,变换不同的窗函数形式,可以使得对信号幅值的估值精度有很大提高,是对谱分析法的改进,解决了非整周期采样造成的频谱泄漏问题。(3)Prony采样法。采用该方法,是为了实现对正弦信号的整周期采样,亦称同步采样法。

图2 比较法校准
谱分析法在理论和实践中主要存在以下问题:
(1)计算原因引起的估值误差;(2)频率分辨力有限的问题;(3)非整周期采样引入的误差;(4)水听器的接收信号有一个稳定过程,传统上,由人工选取稳定区域,再由计算机进行计算,这就导致了稳定区域选择的不确定性,从而产生了谱分析法结果的不确定性。
加窗谱分析法可以在很大程度上提高非整周期采样时对信号幅值的估计精度,Prony采样法实现了信号频率与采样频率的同步,从而实现了整周期采样。然而,这两种方法都无法同时解决上述4个问题。
3 基于曲线拟合法的转移阻抗的测量
3.1 算法原理
曲线拟合法采用如式(4)的信号模型。将信号幅值A、相位φ和频率f看作随机变量,为换能器接收信号建模。根据一系列采样值(t,f(t)),以最小二乘准则,采用非线性拟合的L-M算法求解模型参数,最后以参数的估计值计算转移阻抗。曲线拟合采用Levenberg-Marquardt算法进行参数求解:

3.2 Levenberg-Marquardt算法
在非线性问题的迭代求解过程中,高斯牛顿迭代具有二阶的收敛速度,但迭代过程中的Hessian矩阵又可能变成奇异阵,出现迭代无法进行的局面,因而稳定性较差。Levenberg-Marquardt(L-M)算法则是在高斯牛顿法和梯度下降法之间进行平滑调和,在远离最小值时逐渐切换到高斯牛顿法。它既有高斯牛顿法的局部收敛性,又具有梯度下降法的全局特性[6]。由于L-M算法利用了近似的二阶导数信息,它比梯度法快得多。设x(k)表示第k次迭代的权值和阈值所组成的向量,新的权值和阈值组成的向量x(k+1)可根据下面的规则求得:

设误差函数为

式中:E(x)——误差;
Q——目标向量元素数目。
那么
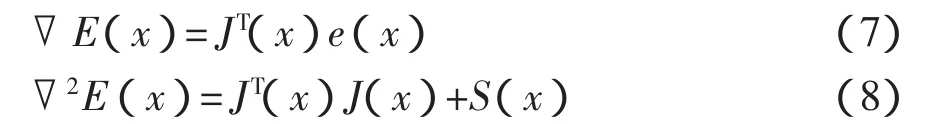
式中:▽E(x)——梯度;
▽2E(x)——E(x)的Hessian矩阵;

对于高斯牛顿法有:

式中:μ——比例系数,常数;
Ⅰ——单位矩阵。
从该式可看出,如果μ=0,则为高斯牛顿法;如果μ取值很大,则L-M算法接近梯度下降法,每迭代成功一步,则μ减小一些,这样在接近误差目标的时候,逐渐与高斯牛顿法相似。实践证明,采用L-M及其改进算法,速度可以比原梯度下降法提高几十甚至上百倍[7-8]。
4 对比实验
实验以NI PXI-5412信号发生器发射不同频率的正弦信号,以NI PXI-6133数据采集卡对其进行采集,然后对幅值进行估计。实验模拟了在实际校准中采样点数的不确定性。如前文所述,采样点数的不同将造成FFT计算时补零个数的不同。
4.1 测量精度
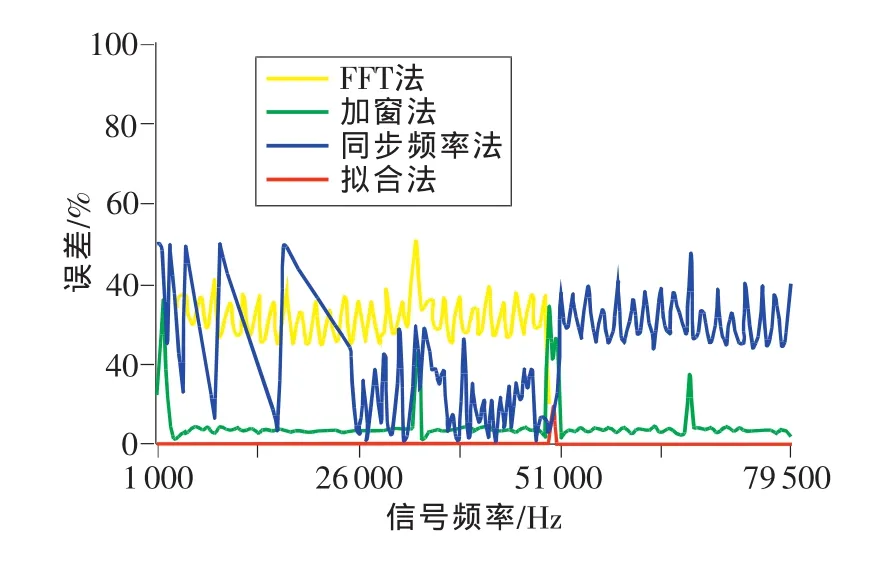
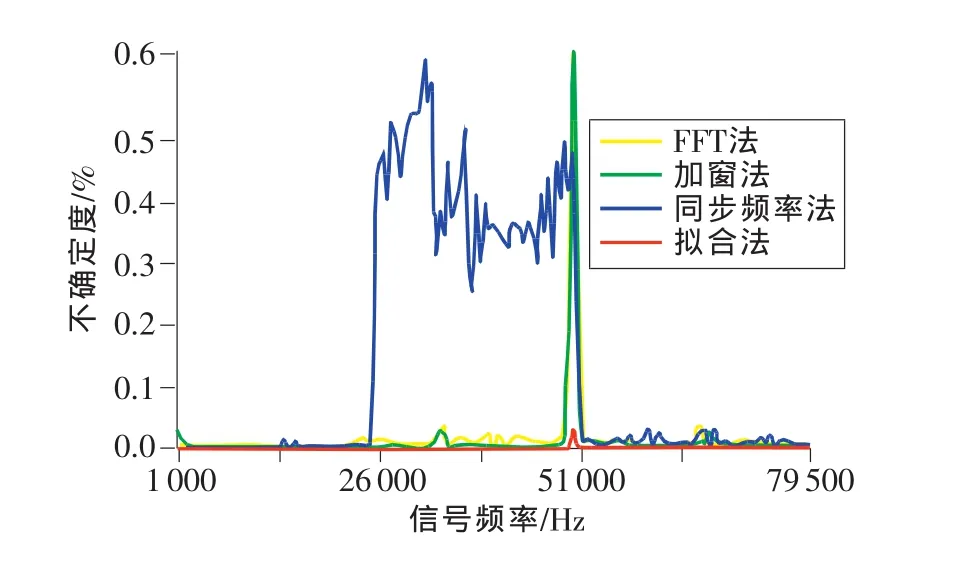
为了对比测量精度,实验以5412信号发生器,发射幅值为1V,频率为1~79.5kHz的正弦信号,信号频率步长为500Hz,用6133数据采集卡对信号采样,采样时间t为满足1ms 从图3、图4中可以看到:(1)谱分析法和Prony采样法,对于信号的采样长度与FFT的点数的对应程度(即需补零的个数)非常敏感,而加窗谱分析法可以有效地改善这一情况,能够给出较准确的幅值估计。对于曲线拟合法而言,这一情况对于幅值的估计不会造成影响,计算精度要高于基于谱分析的各种方法。(2)对于1~2kHz的频段,加窗谱分析法产生了较大的误差,这是由于采得的信号周期过少所致,而曲线拟合法对此情况有很好的适应性。(3)曲线拟合法在50kHz的频率点上出现了较大的误差。此时,采样频率正好为信号频率的2倍,而信号发生器产生的信号初相为0,从而导致所有采样数据均为0,曲线拟合法不能给出准确的估计。对于这种情况,在工程应用中,只需调整采样频率即可。本文将采样频率调整为110 kHz后,可以准确得到50 kHz信号的幅度的估值。(4)在欠采样的条件下(频段为50.5~79.5 kHz),曲线拟合法仍然可以给出准确的估值。 图3 无噪声时的测量值 图4 无噪声时的测量误差 为了研究曲线拟合法对噪声的鲁棒性,对信号加入高斯噪声(σ2=0.03),仍采用前述实验条件,对信号幅值进行估计,结果如图5、图6所示。 可以看出,曲线拟合法对噪声有很好的适应能力,可以满足实际校准的需要。 测量不确定度是表征合理地赋予被测量之值的分散性,与测量结果相联系的参数[9]。校准结果的不确定度反映了对被校量值认识的不确定性,在水声领域中通常用作对校准结果的可靠性度量,是测试方法有效性的重要判据[10]。在4.1节所述条件下,进行了对幅值估计的标准不确定度的比对实验。标准不确定度定义为式(11),测试结果见图7和图8。 图5 加入高斯噪声(σ2=0.03)后的测量值 图6 加入高斯噪声(σ2=0.03)后的测量误差 图7 无噪声时的标准不确定度 图8 加入高斯噪声(σ2=0.03)后的标准不确定度 可以看出:(1)加窗谱分析法和曲线拟合法有较小的标准不确定度,谱分析法和Prony采样法的不确定度变化较大。(2)在加入噪声后,谱分析法、加窗谱分析法和Prony采样法的标准不确定度均有不同幅度的提高,而曲线拟合法的标准不确定度几乎没有变化。(3)在50kHz的频率点上,曲线拟合法出现了较大的标准不确定度,原因亦为采样频率正好为信号频率的两倍所致,改变采样频率为110kHz后,标准不确定度减小。 基于L-M算法的曲线拟合法,在对水声换能器的转移阻抗进行测量计算时,测量精度高,标准不确定度小,在测量计算时,受限条件少,不需满足基于谱分析法的各种方法所需的计算条件,在欠采样的情况下,依然可以获得很高的估算精度和很小的标准不确定度。同时,具有较强的鲁棒性,对噪声适应能力较强,可以满足实际测试校准工作的需求,具有一定的优越性。 [1]王炳辉,陈敬军.声纳换能器的新发展[J].声学技术,2004,23(1):67-71. [2]金晓峰,袁文俊.一种新的水声换能器瞬态校准方案[J].声学学报,1996,21(4):306-312. [3]GB/T 7965—2002声学 水声换能器测量[S].北京:中国标准出版社,2002. [4]GB/T 3223—1994声学 水声换能器自由场校准方法[S].北京:中国标准出版社,1995. [5]郑士杰,袁文俊,缪荣兴,等.水声计量测试技术[M].哈尔滨:哈尔滨工程大学出版社,1995. [6]Hanan M T,Mfnilaj M B.Training forward networks with the marquardt algorithm[J].IEEE Trans on Neural Net,1994,5(6):989-993. [7]王赞松,许洪国.快速收敛的BP神经网络算法[J].吉林大学学报:工学版,2003,33(4):79-84. [8]Toledo A,Pinzolas M,Lbarrola J J,et al.Improvement of the neighborhood based Levenberg-Marquardt algorithm by local adaptation of the learning coefficient[J].IEEE Trans on Neural Networks,2005,16(4):988-993. [9]JJF 1059—1999测量不确定度评定与表示[S].北京:中国计量出版社,1999. [10]杨博,金世俊.基于虚拟仪器的水声换能器校准系统[J].东南大学研究生学报,2007,5(1):58-63.
4.2 测量不确定度



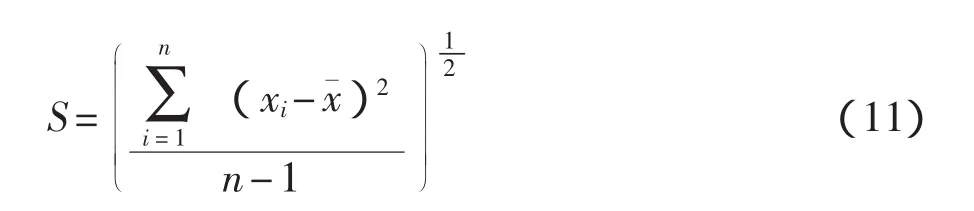
5 结束语
