基于LO-EKF算法的分布驱动电动汽车状态估计的研究*

林 程，王 刚，曹万科，周逢军

(1.北京理工大学，电动车辆国家工程实验室，北京 100081; 2.山东交通学院汽车工程学院，济南 250023)

前言

行驶过程中，车辆的状态变量是实现车辆主动和被动安全控制的主要依据。通常车辆的运动状态变量均可通过传感器测取。然而受到条件的制约，对于某些重要的过程变量，须使用较为昂贵的测试设备来测量，或者根本无法直接测取。因此，国内外学者提出了多种车辆状态软测量法[1-3]。但是，这些算法都是在路面平坦的前提下进行的，实际中车辆行驶的路面坡度是一个时变量，当路面具有一定的坡度时，上述算法的准确性有待提高。

分布式驱动电动汽车的优点为电机驱动转矩和转速可以实时读取[4]。本文中首先提出了基于龙伯格状态观测器的路面坡度实时估计算法，然后基于扩展卡尔曼滤波提出了分布式驱动电动汽车非线性状态估计算法。算法以安装在车辆上的惯性传感器所获取的数据信息作为观测值，对分布式驱动电动汽车的动力学状态变量进行估计并进行仿真分析。与车辆动力学软件Carsim的仿真结果进行比较后，证明以上联合估计算法的可行性和准确性。

1 整车动力学模型的建立

1.1 车辆坡度估计模型

目前国内外对车辆动力学状态估计的研究主要是以在水平路面上的行驶车辆作为研究对象。只有极少数文献考虑了纵向斜坡对车辆行驶的影响。因此，有必要对路面坡度进行实时观测，如图1所示。

虽然可以使用高精度的GPS，通过差分信号的方法进行路面坡度估计，但是花费较多。因此，使用车辆标配的ESP传感器信号来进行路面坡度估计。由于整车的纵向加速度可以通过传感器实时获取，故路面坡度估计方程[5]为

(1)

由于电动汽车的特点：驱动电机的转矩和转速实时可知，驱动轮的纵向力[6]为

(2)

式中：Tx1,2为驱动轮的驱动转矩；J车轮的转动惯量；ω为驱动轮的角速度。

车辆行驶的路面大多为平滑变化的路面，所以，将路面的变化率设定为0。一般情况下，路面的坡度均在10°以下，可以用θ近似代替sinθ。

1.2 四轮车辆模型

忽略滚动阻力和空气阻力，在考虑路面坡度的前提下，建立车辆模型，如图2所示。

其中，四轮车辆的动力学方程请参考文献[7]，在此不再赘述。

值得指出的是，传统的车辆状态估计算法对于车轮纵向附着力的估计均是基于车轮的滑移率，引入半经验车轮模型后计算得到。由于分布式驱动电动汽车驱动电机的转速和转矩实时可知，在不引入轮胎模型的前提下，该算法就可以准确估计驱动车轮的驱动力，提高了估计的准确度和实时性。

2 Luenberger-EKF联合估计算法

2.1 Luenberger状态观测器(LO)

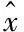
系统的状态方程为

(3)

构成的路面坡度龙伯格观测器方程为

(4)

显然，系统状态方程中的3个矩阵皆可观测。

2.2 扩展卡尔曼滤波算法[9]

卡尔曼滤波用线性差分方程描述离散时间过程的状态变量，然而车辆动力学系统却常常是非线性的。因此，须引入处理非线性系统问题的卡尔曼滤波方法，即扩展卡尔曼滤波。其基本思想是利用泰勒展开式把线性系统在当前状态点展开，舍去二阶及其以上的高阶项，从而把系统进行线性化的近似，具体步骤如下。

预测阶段：利用上一时刻车辆扩展状态变量的估计值及其协方差矩阵来估计当前时刻状态变量及其误差协方差。

(5)

式中：g(·)为估计系统的扩展形式的状态方程。A为系统方程对状态矢量求偏导的雅克比矩阵。

更新阶段：利用传感器在t=k时刻的真实测量值来修正上一步的预测值：

(6)

式中：h(·)为系统的量测方程，zk为当前时刻传感器测量到的量测矢量；Kk为当前时刻的卡尔曼增益；C为量测方程对状态矢量求偏导的雅克比矩阵。

由以上状态空间模型可得，系统的状态变量为

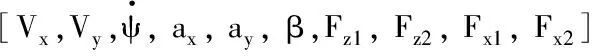
系统的观测变量为

3 路面坡度和车辆状态估计仿真研究

采用车辆动力学软件CarSim进行仿真试验，验证路面坡度和车辆状态估计算法的准确性和有效性。试验中车辆参数的设置与本文的目标车辆相同，将转向盘转角和油门踏板行程作为估计算法的输入量；在考虑了车辆ESP标配传感器的前提下，将车辆纵向加速度、横向加速度、横摆角速度和车轮转速作为估计算法的量测值；将软件输出的车辆质心侧偏角、纵向车速、横向车速、车轮的纵向力等数据与通过估计算法得到的估计值进行比较验证。整车参数如下：

M=1 750kg,a=1.33m,b=1.27m,h=0.45,

IZ=3 200kg·m2,tf=td=1.6m,r=0.31

3.1 路面坡度估计仿真

选取原地直线起步工况和直线加速工况。直线加速工况初速为36km/h，选择两种坡度路面(单一路面和坡度线性变化路面)。其中，单一路面的坡度为5°；线性变化路面的坡度呈线性变化，每米坡度增加0.2°。仿真结果如图3～图6所示。

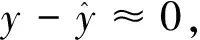
设计的具有Luenberger类型反馈环节的非线性观测器，利用车载传感器测量值与车辆模型输出值之间的偏差作为观测器的反馈项。仿真结果表明，该方法基本达到了估计目标。另外，上述路面坡度估计方程没有考虑车辆的俯仰角和侧倾角，实际中二者会降低该非线性观测器的估计精度。本节的目的是为了提高车辆在非平坦路面上行驶时的车辆状态估计算法的精确性，可忽略以上因素的影响。

3.2 车辆状态估计仿真

选取以下两种实验来进行仿真分析：高附着路面双移线实验和低附着路面直线加速实验。高附着路面附着系数为1；低附着路面附着系数为0.2。双移线实验场地按照ISO 3888—1—1999标准中的要求设置，坡度为常数5°。

(1)高附着系数路面双移线实验

实验结果如图7所示。各分图中的横坐标为样本点序号。实线为车辆的状态实际值，虚线为估计值。由图可见，车辆的纵向车速估计值与实际值的误差最小，这与初速度值选取的是非驱动轮的轮速值有很大关系。横向车速的估计值虽与实际值有一定的偏差，但是总体的变化趋势大致相同。前轴左右车轮的纵向力估计值基本跟踪了实际值，并围绕试验值小幅波动。波动的原因是由于输入的纵向加速度本身有波动而引起，但随着横向运动的减弱，估计值和实际值逐渐接近。所以，当车辆在沥青路面上进行双移线实验时，在初值设置合理的情况下，收敛速度很快，估算精度的误差在±5%范围内，达到规定要求。

(2)低附着系数直线加速实验

实验结果如图8所示。各分图中的横坐标为样本点序号。实线为车辆的状态实际值，虚线为估计值。由图可见，当初速度较低，油门踏板行程较小，车辆在附着系数为0.2的路面(积雪路面)上行驶时，前轴左右车轮的纵向力和垂向载荷估计值很好地跟踪了实际值，趋势一致，估计效果理想。

由于本文中使用的车辆状态估计算法主要为后续分布式驱动电动汽车的纵向行驶时驱动防滑控制提供重要依据，所以仅列出了与驱动轴纵向运动相关的状态估计量。

4 结论

(1)在车辆状态估计算法中，考虑了路面坡度的影响，并提出了基于龙伯格观测器的路面坡度实时估计算法。为后面的车辆状态估计算法提供了依据。对提高基于模型的车辆动力学控制系统的鲁棒性具有重要意义。

(2) 建立了整车模型，比较CarSim软件输出值与估计算法的值，表明Luenberger-EKF对道路坡度和车辆状态变量的估计达到了较好的精度。

(3) 充分利用电动汽车的驱动电机的转矩和转速可以实时获取的特点。在无须采用半经验轮胎模型的前提下，可精确估计轮胎的纵向力，为车辆的牵引力控制提供可靠依据。

(4)需要说明的是，本文中通过仿真对算法进行验证。在仿真环境下，车辆的驱动转矩是准确实时可知的。但是，由于目前制造水平的限制，在实际应用中，车辆驱动电机的转矩在不安装外置转矩传感器的前提下，仅仅通过电机控制器反馈回来的电机转矩值或者通过电机的输入电流、电压等数值进行换算后得来的数值，较实际值均有较大的误差。这势必会影响算法在实际应用中的估计精度。结合本试验室的研究情况，可在驱动电机装车前，进行电机特性的台架试验，得到电机的相关特性参数。在后续实际应用中，可通过直接查表的方法确定车辆的驱动转矩值，该方法较为可行。

[1] Satria M, Best M C. State Estimation of Vehicle Handling Dynamics Using Non-linear Robust Extended Adaptive Kalman Filter [J]. Vehicle System Dynamics, 2004, 41(S) :103-112.

[2] 高振海, 郑南宁, 程洪. 基于车辆动力学和Kalman滤波的汽车状态软测量[J]. 系统仿真学报, 2004, 16:22-24.

[3] Ray L R. Nonlinear Tire Force Estimation and Road Friction Identification[J]. Simulation and Experiments, Automatica,1997,33(10):1819-1833.

[4] Yozo Hori. Future Vehicle Driven by Electricity and Control-research on Four-wheel-motored “UOT Electric March II”[J]. IEEE Transactions on Industrial Electronics, 2004, 51(5):954-962.

[5] 余志生. 汽车理论[M]. 北京：机械工业出版社，2006：20-25.

[6] Rajamani R. Vehicle Dynamics and Control[M]. New York:Springer, 2005:99-108.

[7] Kiencke U, Nielsen L. Automotive Control Systems[M]. Berlin:Springer, 2000:50-54.

[8] Luenberger D G. An Introduction to Observers[J]. IEEE Transactions on Automatic Control, 1971,AC-16(6):596-602.

[9] Simon Haykin. Kalman Filtering and Neural Networks[M]. New York:John Wiley & Sons, 2001:16-20.