基于随机模型预测控制的并联式混合动力汽车控制策略研究*
2014-02-27赵韩,吴迪
赵 韩,吴 迪
(合肥工业大学机械与汽车工程学院,合肥 230009)
前言
混合动力汽车将发动机、电机和电池组合在一起,可以很好地发挥发动机和电机的优势,有效实现节能减排。混合动力汽车的控制策略是影响其燃油经济性和排放的关键技术,目前应用较多的是基于规则的控制策略,包括基于逻辑门限值的控制策略等,这一类控制算法简单、实时性好,但是其设计往往依赖于经验,很难保证最优的效果[1]。另外,动态规划方法也常被用来解决混合动力汽车的优化控制问题,由于动态规划受限于特定工况,且计算量很大,因此无法单独应用于车辆的实时控制[2]。
为更好地实现对车辆混合系统的控制,近年来国内外一些学者利用模型预测控制方法预测汽车在未来时间域内的动力需求,并进行优化得到转矩分配比等变量。文献[3]中在2009年提出一种指数函数预测方法,并将混联式混合动力汽车的非线性优化方法简化为线性MPC模型进行优化。文献[4]中提出在GPS等获取的信息基础上,结合动态规划方法进行优化管理,得到最优转矩分配策略。文献[5]中利用模型预测控制方法对并联混合动力汽车的换挡策略、转矩分配策略进行研究。
本文中提出一种基于随机模型预测控制的控制策略,它是对模型预测控制方法的延伸,该方法将驾驶员功率需求的预测视为一个具有马尔科夫性质的随机过程,通过建立马尔科夫模型得到未来的驾驶员需求功率,并进行滚动优化。
1 并联式混合动力汽车动力学模型
本文的研究对象为某并联式混合动力汽车,其动力系统结构如图1所示。发动机通过离合器与电机相连,再通过传动系将动力传至车轮,当离合器闭合时,发动机与电机同轴转动。在并联式混合动力汽车中,发电机一般作为两用:当其作为电动机时,电池放电提供电能;当其作为发电机时,电池处于充电状态。
汽车动力学方程如下:
(1)
Twheel=Treqi+Tb=(Te+Tm)i+Tb
(2)
(3)
Preq=Treqne/9550
(4)
式中:Twheel为车轮需求转矩,N·m;m为汽车的整备质量,kg;g为重力加速度,m/s2;CD为风阻系数;A为迎风面积,m2;δ为旋转质量换算系数;θ为坡道角度,(°);μ为滚动阻力系数;r为车轮半径,m;v为车速,m/s;Treq为动力源需求转矩,N·m;Te为发动机转矩,N·m;Tm为电机转矩,N·m;Tb为摩擦制动器在车轮上的制动力矩,N·m;i为传动比;ne为发动机转速,r/min;nm为电机转速,r/min;Preq为驾驶员需求功率,kW;t为时间。
当电机用作电动机时,其所需功率为
(5)
当电机用作发电机时,其发电功率为
(6)
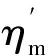
2 驾驶员需求功率的随机模型
在车辆实际行驶过程中,驾驶员通过操纵油门踏板和制动踏板来表达功率需求,其值是不可知的,但可将其视为具有马尔科夫性质的随机过程,即下一时刻的需求功率只和这一个状态的需求功率有关,与之前的状态无关。而其转移概率可以通过统计标准循环工况下的功率需求来获得。
将功率需求离散为有限个数的一数列[6]:
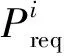
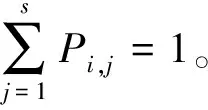
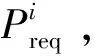
图3为通过统计UDDS工况和NEDC工况得到的转移概率矩阵。在本文中选取s=16。
3 PHEV的随机模型预测控制
并联式混合动力汽车的控制策略可以看成是一个以电机/发动机的转矩分配为控制变量的多目标优化问题,其优化目标包括燃油消耗和电池SOC平衡。由于在预测区间内总的需求转矩已知,因而只要确定了发动机转矩,电机转矩即可确定,反之亦然。因而在本文中选取电机转矩为控制变量,电池荷电状态SOC为状态变量。
3.1 应用随机模型预测控制的步骤
在应用模型预测控制过程中,通常优化不是一次离线进行的,而是在线反复优化,即滚动优化,也是模型预测控制方法区别于其他控制方法的根本特点[7]。
模型预测控制的基本步骤如下[8]:
(1)如上所述,根据某采样时刻k的需求功率和速度,由驾驶员需求功率的随机模型得到未来p时间的功率需求预测序列,并根据式(1)~式(4)计算出在预测时间区间内对应的动力源转矩需求、转速和车速;
(2)根据上述结果,在该预测时间区间,即[k,k+p]内进行优化,得到最优控制变量,即最优电机转矩序列[u(k+1),u(k+2),…,u(k+p)];
(3)应用该最优电机转矩序列的第一步,并进入到下一采样时间,重复上述步骤。
由上述步骤可以看出,应用随机模型预测控制是一个滚动优化、滚动实施的过程,这使其优化的区间变小,可在很大程度上减小其优化的计算量,缩短优化时间,使之可以应用于在线仿真。
3.2 动态规划方法
前言中曾指出,动态规划由于计算量很大,无法单独用于车辆的实时控制;但在随机模型预测控制中,对预测时间内转矩分配的计算,计算量已大幅度减小,因而在此局部地应用动态规划。动态规划方法适合求解有约束的非线性最优化问题[9]。在采样时刻k,通过随机模型可得到在[k,k+p]区间内的驾驶员需求功率序列,进而可以得到该区间的需求转矩和转速序列,因而在[k,k+p]内的优化问题就是一个有约束的非线性最优化问题,因而选用动态规划方法对该优化问题进行求解以得到在该区间内的最优控制变量向量。
将电池模型简化,忽略温度对电池的影响,则电池SOC变化方程为
(7)
其中
式中:I为电池的内部电流,A;SOC1为初始SOC值;C为电池容量,A·h;U为电池的端电压,V;R为电池内阻,Ω;P为电池充电或放电功率,W,它应等于电机的充电功率或放电功率,可通过式(5)或式(6)计算得到。电池的端电压和内阻可分别通过SOC插值得到,开路电压、内阻与SOC的关系分别如图4和图5所示。
混合动力汽车的主要优化目标为混合动力汽车的油耗;另外为了延长电池的使用寿命,使电池工作在一个效率较高的工作范围内,希望将SOC限制在某一期望值附近范围内,因而将电池SOC平衡作为另一个优化目标,所以设定每一阶段的目标函数为
L(x(k),u(k))=wfmf(k)+wsoc(SOC(k)-SOCr)2
(8)
式中:mf为燃油消耗率,g/s;wf和wsoc分别为燃油消耗电池SOC与其期望值差值的加权因子;SOCr为期望的SOC值,选取SOCr=0.6。
根据Bellman最优化原理,在预测时间区域[k,k+p]内进行逆向计算,逐步计算其在预测时间区域内的最优控制解[10]。
j=k+p-1,k+p-2,…,k+1,k
(9)
则最优控制解可由下式获得:
通过采样时刻的SOC插值即可得到其第一步的最优控制变量,即最优控制电机转矩,并根据式(7)得到下一采样时刻的SOC值。
为防止电池的过充或过放,须使电池的SOC限定在一定范围内。而在k时刻的转速为n(k)条件下,发动机和电机的输出转矩受其转速特性的限制,综上所述,其约束条件[9]为
(10)
式中:SOCmin(k)和SOCmax(k)分别为k时刻电池SOC可达到的最小值和最大值;Te_max(n(k))和Te_min(n(k))分别为发动机转速为n(k)时的最大输出转矩和最小输出转矩,N·m ;Tm_max(n(k))和Tm_min(n(k))分别为电机转速为n(k)时的最大输出转矩和最小输出转矩,N·m。
在利用动态规划进行计算时,为了减小计算量,提高计算效率,可以缩小其状态量即SOC的范围来进行。在每一采样时刻的SOC值已知且预测时间内的电机最大放电功率和充电功率可根据转速插值计算得到的情况下,计算出预测时间内的电池SOC可达范围,进而大大缩小SOC的范围,可使计算效率有很大程度地提高。
4 仿真结果分析
基于随机模型控制算法,编写m程序,实现其滚动优化功能。在Matlab/Simulink平台上建立仿真模型,以路况信息为输入,并利用s-function调用该m程序进行仿真,以得到其电机/发动机转矩分配策略和SOC值的变化情况。
4.1 混合动力汽车主要参数
该混合动力汽车主要参数如表1所示。
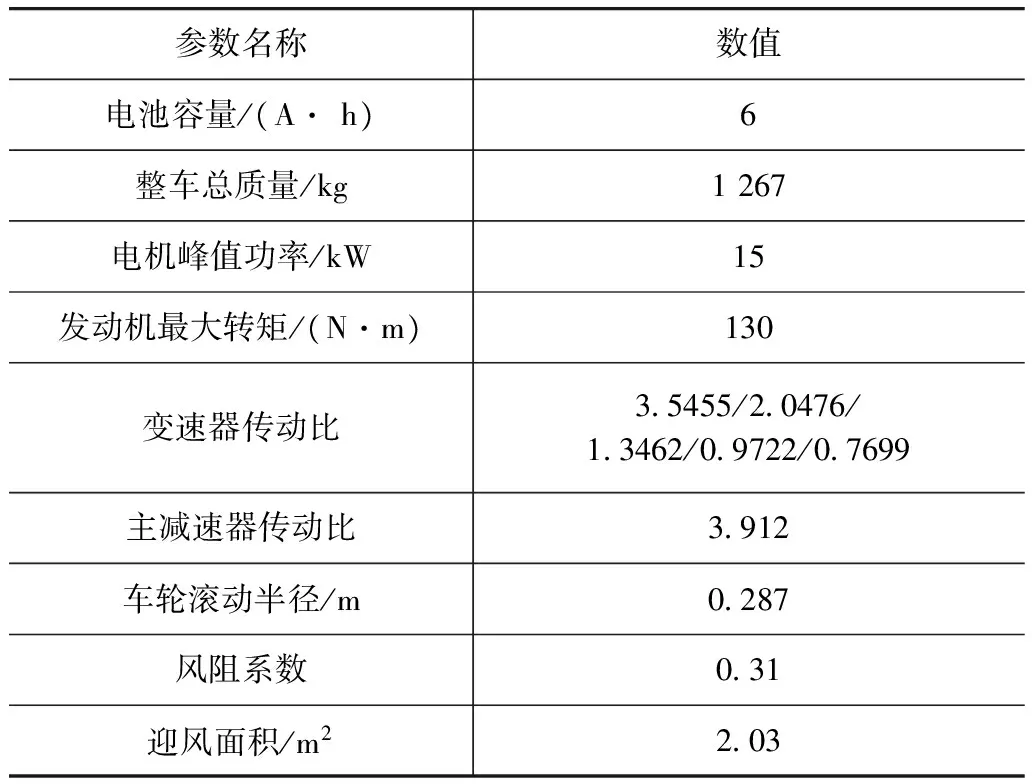
表1 PHEV主要参数
4.2 仿真结果分析
在目标函数的加权因子选取时,考虑到发动机在较低负载时效率较低[11],所以在较低负载时选取油耗的加权因子相对较大,使之尽量使用电机驱动;另外,在较高负载时,发动机油耗较大,为使电机全力辅助驱动,也应取较大的油耗加权因子,具体规则如下所示:
IfTreq(k)>65
wsoc=1,wf=1
elseif 30 wsoc=1.8,wf=0.001 elseif 15 wsoc=1,wf=0.003 elseif 0 wsoc=1,wf=0.05 elseifTreq(k)≤0 wsoc=0,wf=1 在本文中,选取预测时间p=8,另外选取两种预测方法与基于随机模型预测控制的控制策略进行对比。第1种预测方法为在预先知道未来路况的基础上,根据已有的知识得到未来的功率需求;第2种预测方法为恒值预测方法,即认为在未来预测时间内,其需求功率保持不变且等于采样时刻的需求功率。分别根据这两种预测方法编写m程序,并通过仿真模型调用程序,在NEDC工况下,对基于3种方法的控制策略进行仿真,结果如图6所示。图6(a)为汽车在该工况下动力源的需求转矩,图6(b)为基于随机模型预测控制方法所得到的发动机控制转矩,图6(c)为基于具有预先知识的预测方法所得到的发动机控制转矩,图6(d)为基于恒值预测方法所得到的发动机控制转矩,图6(e)为基于3种不同预测方法的油耗。由图6(e)可知,虽然基于随机模型预测控制算法得到的控制策略在该工况下的油耗相比于有预先知识的预测方法略高,但是其结果明显优于恒值预测方法,三者的油耗差别是由于基于不同预测控制方法所得到的发动机控制转矩不同造成的,通过对比图6(b)~图6(d)即可看出发动机控制转矩的不同。由于具有预先知识的预测方法在预测区间内的需求功率与实际需求功率相同,所以其所得到的转矩分配策略相对较优,即油耗较低;而随机模型预测方法则是根据总结多个循环工况下的功率需求进行预测的,其预测得到的需求功率与实际情况不一定相同,但是其通常与实际的功率需求变化趋势接近,而恒值预测方法是认为在预测区间内需求功率不变,其在多数情况下并不能反映需求功率的变化情况,所以基于随机模型预测控制下得到的转矩分配策略油耗相比与基于预先知识的预测控制策略略高,却比基于恒值预测控制策略要低。所以,在未来路况未知的情况下,基于随机模型预测控制的控制策略具有很好的燃油经济性。 基于随机模型预测控制的转矩分配结果及SOC变化情况如图7所示。 在NEDC循环工况下,该混合动力汽车燃油总消耗量为453.36g,该循环工况总里程为11.01km,工况结束时的SOC为0.579,故其等效100km油耗为5.82L,而在ADVISOR里对基于门限值控制策略的并联式混合动力汽车参数进行修改,仿真得到其100km油耗为6.23L,因而基于随机模型预测的控制策略与逻辑门限值控制策略相比,燃油经济性提高了7.04%,表明采用随机模型预测控制进行转矩分配具有显著的节油效果。该工况总时长为1 180s,进行离线仿真总时间需要14min,说明其具有良好的实时性。 控制策略是混合动力汽车的核心技术之一。提出一种基于随机模型预测控制算法的控制策略,将驾驶员需求功率视为马尔科夫随机变量。通过对现有标准工况进行统计获得其需求功率的统计特征,并基于预测得到的需求功率进行滚动优化,得到基于随机模型预测的控制策略。在Matlab/Simulink平台上搭建仿真模型, 基于标准路况进行仿真分析,并与恒值预测的方法和有预先知识的预测方法的结果进行对比。结果表明,它不仅具有较好的燃油经济性,同样具有很好的实时性,证明了基于随机模型预测的控制策略是可行的,并可应用于硬件在环仿真。 [1] 邹渊,陈锐.侯仕杰.基于随机动态规划的混合动力履带车辆能量管理策略[J].机械工程学报,2012,48(14):91-96. [2] 申彩英.串联混合动力汽车能量优化管理策略研究[D].天津:天津大学,2010. [3] Borhan H, Vahadi A, Philips A. Predictive Energy Management of a Power-split Hybrid Electric Vehicle[C]. 2009 American Control Conference. St.Louis,2009:3970-3976. [4] 舒红,蒋勇,高银平.中度混合动力汽车模型预测控制策略[J].重庆大学学报,2010,33(1):36-41. [5] Ngo V, Hofman T, Steinbuch M, et al. Predictive Gear Shift Control for a Parallel Hybrid Electric Vehicle [C]. 7th IEEE Vehicle Power and Propulsion Conf, Chicago,2011:1-6. [6] 张炳力,代康伟,赵韩.基于随机动态规划的燃料电池城市客车能量管理策略优化[J].系统仿真学报,2008,20(17):4664-4667. [7] 邹涛,丁宝苍,张端.模型预测控制工程应用导论[M].北京:化学工业出版社,2010. [8] Yan Fengjun, Wang Junmin, Huang Kaisheng. Hybrid Electric Vehicle Model Predictive Control Torque-Split Strategy Incorporating Engine Transient Characteristics[J]. IEEE Transactions on Vehicular Technology,2012,61(16):2458-2467. [9] 张博,李君,高莹,等.Plug- in混合动力汽车能量管理策略全局优化研究[J].中国机械工程,2010,21(6):715-720. [10] 张炳力,张平平,赵韩,等.基于离散动态规划的PHEV燃油经济性全局最优控制[J].汽车工程,2010,32(11):923-927. [11] 孙四军.基于混合动力系统效率的发动机工作点的控制[J].汽车工程,2012,34(3):207-210.5 结论
