渗流-切向水流耦合作用下多孔介质水动力试验

谢立全，朱晔慧，黄文锐，张 毅

（同济大学 土木工程学院，上海200092）

在山坡、江河底床、近海及海洋底床等大自然广泛存在着松散的多孔岩土介质，其水土流失规律与作用于表层土体的水流条件［1］、多孔介质内的孔隙水流动［2］息息相关.国内外已有大量学者对此开展研究，取得的成果已从床面水流摩阻力研究发展到了多孔介质内部孔隙水的水动力分析.Beavers等［3］在对比分析多孔介质与不透水床面受到的水流摩阻力基础上指出多孔介质的透水特性可削减切向摩阻力.Jolls［4］对多孔介质内部的流动特征进行了试验分析，并建立了与颗粒直径雷诺数之间的函数关系.Wallace等［5］、Willmarth等［6］采用热线测速技术和象限仪研究了紊流边界层的相干结构.Antohe等［7］建立了稳态充分发展流动的简化湍流模型，并指出稳态充分发展湍流流动时，多孔介质内不存在宏观湍流，只有孔隙微观湍流.Breugem等［8］对多孔介质表面的紊流进行了细致的数值模拟分析.马坤［9］研究了多孔介质固体骨架形状对多孔介质内湍流流场的影响.

然而，作为多孔介质的表层岩土散粒体往往同时受到切向水流和渗流的耦合水力作用［10］，比如受强烈潮汐影响的滩岸、受风暴潮影响的海床，其渗流与床面切向水流相互影响、共同作用于床沙土体，对床面泥沙输移产生重要影响，使得水沙界面处的水动力现象更加复杂多变.因松散土体不断被水流带走而使得水沙界面呈现为动态变化的特点，这已引起了国内外学者的关注.Ruff等［11］对透水河床内部与表面的紊流切应力进行了研究.Suga等［12-13］采用粒子图像测速（PIV）技术研究了多孔介质的渗透性能对透水河床明渠紊流的影响.多孔介质在切向水流与法向渗流二者共同作用下，其内部孔隙水的流动特征将会发生改变，目前尚缺乏系统的研究.对此开展研究将有助于进一步完善水沙界面处的泥沙输移机理和水土流失理论.本文以规则排列的均匀球体模型模拟多孔介质，对渗流-切向水流耦合作用下的多孔介质水动力特征进行了直观的试验分析.

1 试验装置

为定量研究切向水流和法向渗流对多孔介质内部孔隙水流动的影响，需采用专门的研究模型装置.试验装置和原理如图1和图2，试验装置由稳流供水箱、渗流供水箱、水槽、尾水箱、水循环管路和塑料圆珠底床等组成.水槽长180cm，宽14cm，水流循环动力由水泵提供.水槽入口端设置栅栏，使水流从供水箱平稳进入水槽，形成明渠均匀流.水槽出口端设置薄壁堰，通过调整堰高控制水槽中的水流深度.试验中采用直径12mm的塑料珠铺设多孔介质底床，模拟具有透水性能的底床.为便于试验观测和结果的可重复性，试验段的塑料珠铺设采用规则排列，即以立方堆积形式排列，孔隙率为0.48，而试验段的上、下游底床均以相同直径的玻璃球随机铺设.试验段长50cm，位于水槽中部，由规则排列的球体构成，球体共堆积5层（如图2）.

图1 试验装置平面布置示意（俯视）Fig.1 Schematic view of the experimental setup（top view）

图2 试验原理示意Fig.2 Test principles

图2给出了渗流-切向水流耦合作用下的多孔介质水动力实验原理，即透水底床同时受到上表面的切向水流和来自底部的法向渗流（向上）作用.试验中渗流供水箱中的水位保持恒定，且进入渗流稳压室后再均匀地渗入多孔介质，以实现均匀的恒定渗流条件.调整渗流供水箱与水槽中的水位落差，即可获得不同强度的渗出水量.渗流稳压室位于水槽底部，净空高度为5cm，由隔板将多孔介质与底部渗流供水隔开.隔板仅在试验段具有透水性，将隔板钻孔而实现均匀的法向渗水条件，孔径1.5mm，小孔均匀布置在规则排列的球体之间（如图3）.

图3 墨水迹线法示意（侧视）Fig.3 Schematic view of dye injection（side view）

2 试验内容

在恒定的水槽流量1.49L·s-1条件下，改变出口堰顶高度、渗流供水箱-水槽水位落差，共进行了8个工况的试验，具体见表1.H为水深，指水槽中的自由水面与球体顶部所在平面的垂直距离.Q为渗流强度，即从渗流稳压室进入多孔介质的法向渗出水量，为单位时间内透过隔板单位面积的法向渗出水量.试验中采用墨水迹线法和多孔介质内部孔隙水的动压监测2种方式，对法向渗流与切向水流耦合作用下的多孔介质孔隙水动态响应进行分析.

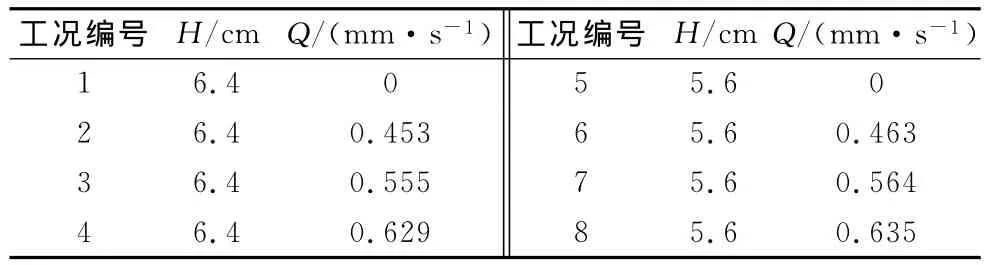
表1 试验工况Tab.1 Hydraulic conditions for the experiments

墨水迹线法曾较多应用于流场分析，可直观再现流场特征.本文采用注射器汲取墨水后，针头竖直向下从试验段球体的孔隙中探入，在不同的深度处连续释放墨水（见图3、图4），观测墨水迁移、消散特征.试验过程中始终保持注射器针孔朝向下游，针头探入的位置选在试验段中部，以避免试验段两端边界效应的影响.

图4 墨水迹线法试验照片Fig.4 Photo of dye injection

多孔介质内部孔隙水的动压采用日本东京测器株式会社PDA-200KPA型压力计进行测试.压力计的量程为200kPa，精度可达0.01kPa.将4个压力计分别固定在试验段第1～4层球体底部最大孔隙处（如图5），压力计的安装含面向来水方向、水槽侧壁2种方式，分别监测明渠流径流向的动水压力与侧向动水压力.数据采样间隔均为50ms，采样总时长为25s，每种工况采集500个水压力值.

图5 压力计布置位置示意（俯视）Fig.5 Details of pressure gauge setup（top view）

3 试验结果与分析

3.1 多孔介质内外水体交换特点

图6为工况4第1、第2层球体底部孔隙处的墨水迹线照片.从照片中可以看出，上层孔隙的墨水迹线更光滑，且快速进入切向主流区.图7给出了工况1～4的墨水迹线照片，可见无论是否有法向渗流，多孔介质内的墨水在球体孔隙之间穿行一段距离后，均从球体之间穿出，进入球体上方的主流区，并很快扩散消失.该现象说明了，多孔介质内外存在明显的水体和能量交换.基于该试验条件下的水不可压缩特性可以认为多孔介质中的孔隙水总体积不变，因此，同一时间内从切向主流区进入多孔介质的水量应该与渗出多孔介质进入主流区的水量严格相等.在多孔介质的孔隙内部，由于流体微团的运动受到上部主流区以及相邻孔隙中水动力的影响，具有一定的随机性与紊动性，因此可以认为该墨水迹线并非流场方向的表征.墨水迹线均主要表现为向上部主流区迁移，而不是向多孔介质内部迁移，且墨水进入主流区后，很快扩散消失，这说明表层孔隙水与主流区之间的水体交换远比多孔介质内部孔隙之间的水体交换要强得多，即主流区紊动强度远比多孔介质内大得多.

图6 工况4第1，2层球体墨水迹线法试验结果Fig.6 Results of dye injection（Case 4）

图7 工况1～4墨水迹线法试验结果Fig.7 Results of dye injection（Case 1～4）

3.2 法向渗出水量的影响

比较图7中的4种工况可知，渗流强度对多孔介质的内外水体交换速率有着明显的影响.随着渗流强度的增大，墨水迹线在孔隙内穿行的距离逐渐从3～4倍球体直径缩短至1倍球体直径，即孔隙水渗出速率成倍增加.同时，也可以看出，存在一个临界渗流强度，渗出水量只有达到该临界渗流强度以后才会明显改变多孔介质孔隙水渗出速率.工况1～4中的临界渗流强度约为0.4mm·s-1.

3.3 水深的影响

以工况2和工况6为例进行对比分析，其渗流强度近似相同.图8为其结果对比图.从图可见，2种工况的迹线在孔隙间穿行的距离大致相等，都为3倍球体直径左右，但工况2的迹线明显比工况6平滑.这说明2种工况下孔隙内流体、动量交换情况相差无几，但工况2中的孔隙内流场更为稳定，紊动强度更小，工况6中的紊动强度相对较大.类似地，将工况1与5、工况3与7、工况4与8对比，也有相似现象.因此，在流量相同情况下，纵向水流的水深与孔隙内紊动强度呈负相关关系.以上现象的一种可能解释是，水深降低导致流速增大，进而水流雷诺数提高，流场紊动性增加，流态紊乱.

图8 工况2与工况6墨水迹线法试验结果Fig.8 Results of dye injection（Case 2and Case 6）

3.4 多孔介质表层孔隙水流动的动水压力特性

在上述直观的迹线试验基础上，运用动态应变仪监测各孔隙内的动水压力，压力计面向上游放置，测定径流方向动水压力.在进行试验前，先将水槽内保持静水状态，并将水位调整至与动水试验相同，进行基准压力标定试验，测定出各水位下各水深处的静水压力值.将试验所得水压力值减去基准压力标定试验的结果，即得到各工况下的动水压力值.

3.4.1 径流方向动水压力随深度变化的特点

以工况4为例，比较不同高度位置的孔隙内动水压力的变化情况.图9为其试验结果对比图.从图可知，4条曲线均较水平，说明在此时段各孔隙中水流较为均匀、稳定.其次，随着深度的增大，孔隙内的动水压力逐渐减弱，说明孔隙内的平均流速随孔隙所在深度的增大而逐渐降低.这一现象与Pokrajac等［14］的研究成果相吻合.其中，第4层孔隙动水压力虽然接近于零，但仍然有波动，其主要原因是该位置靠近渗流稳压室的隔板，从隔板向上渗出的水流对附近孔隙动水压力产生了扰动.

此外，分别取这4层孔隙所测得动水压力的中位数绘制成折线图（图10），然后将第2、第3层孔隙数据点的连线进行反向延长（图中虚线）.从该非线性图可知，相邻数据差值逐渐减小，即上下相邻2层孔隙之间的动水压力变化值逐渐减小，说明孔隙内紊动强度随深度增加而减小的幅值是不均匀的.

图9 不同深度孔隙径流方向动水压力对比Fig.9 Comparison of streamwise hydrodynamic pressure between different pores

图10 不同深度孔隙径流方向动水压力中位数Fig.10 Median of streamwise hydrodynamic pressure among different pores

3.4.2 横断面方向动水压力随深度变化的特点

为测定侧向动水压力，将压力计面向侧壁放置.比较工况1～4的测试结果，其对比情况如图11.从图可见，4条曲线相互交织在一起，曲线振幅约为0.1 kPa.这说明不同渗流条件对侧向动水压力的影响不显著.

图11 不同渗透强度下孔隙侧向动水压力对比Fig.11 Comparison of transverse hydrodynamic pressure between different seepage water heads

4 现象解释

图12示意了渗流-切向水流耦合作用下多孔介质水动力机理的一种可能解释.在渗流和水流共同作用下，渗流通道出口处产生局部微涡和低压区.正是由于局部微涡的产生，使得多孔介质孔隙水的流动变得复杂.即使渗流为零，孔隙水也会有部分渗出进入主流区，同时也有主流区的水进入多孔介质，这就形成了多孔介质水体与主流区的水体交换.渗流的存在使流出的水量多于流入的水量.

墨水迹线所呈现的流场表征的是多孔介质孔隙流体的局部水动力特征.从图12可见，2个固体圆球之间的竖向孔隙间既有从主流区进入多孔介质内部的水流，也有从多孔介质进入主流区的水流.由图7可见，若渗流强度较小，则孔隙水体渗出速率并不能明显增加，由图12的分析可知，渗流阻碍了主流区水体进入多孔介质的渗入速率，从而实质上呈现为水体交换中的渗出速率大于渗入速率.当然，随着渗流强度的增加，超过某一个临界值，则可能明显增强多孔介质中孔隙水体的渗出速率.

5 结论

（1）由等径球体构成多孔介质，其紧邻表层的孔隙内水的流速与紊动强度远小于顶层球体以上的切向主流区，这与国外现有研究成果相符.

（2）在水深、径流流量相同的情况下，随着渗流强度的增大，多孔介质孔隙水渗出速率逐渐增大.

（3）在相同水动力条件下，孔隙内动水压力和紊动强度随孔隙所在深度的增大而逐渐降低，且孔隙内动水压力随所处位置深度的增加而减小的程度是不均匀的，紊动强度的减小幅度逐层减小.

（4）在水深、径流流量相同的情况下，不同渗流条件对相同位置的孔隙侧向动水压力的影响不显著.

水流-渗流相互作用的水沙界面问题非常复杂，本文仅对以等径球体模拟的多孔介质的渗流-切向水流耦合作用进行了定性的规律分析.真实土体中的水流渗流耦合作用的流场结构不仅取决于渗流-切向水流的耦合关系，也与颗粒级配、颗粒形状、颗粒直径等泥沙物理特性有关.本文的研究与真实土体的情况相去甚远，尚有大量问题需要研究.

［1］ Nagata N，Hosoda T，Muramoto Y.Numerical analysis of river channel processes with bank erosion［J］.Journal of Hydraulic Engineering，ASCE，2000，126（4）：243.

［2］ 周念清，李彩霞，江思珉.普定岩溶区水土流失与土壤漏失模式探讨［J］.水土保持通报，2009（1）：47.ZHOU Nianqing，LI Caixia，JIANG Simin.Models of soil and water loss and soil leakage in Puding Karst Area［J］.Bulletin of Soil and Water Conservation，2009（1）：47.

［3］ Beavers G S，Joseph D D.Boundary conditions at a naturally permeable wall［J］.Journal of Fluid Mechanics，1967，30：197.

［4］ Jolls K R.Transition to turbulence for flow through a dumped bed of spheres［J］.Chemical Engineering Science，1966，21：1185.

［5］ Wallace J M，Eckelmann H，Brodkey R S.The wall region in turbulent shear flow［J］.Journal of Fluid Mechanics，1972，54：39.

［6］ Willmarth W W，Lu S S.Structure of the Reynolds stress near the wall［J］.Journal of Fluid Mechanics，1972，55：65.

［7］ Lage J L，Antohe B V，Nield D A.Two types of nonlinear pressure—drop versus flow-rate relation observed for saturated porous media［J］.ASME Journal of Fluids Engineering，1997，119：700.

［8］ Breugem W P，Boersma B J，Uittenbogaard R E.The influence of wall permeability on turbulent channel flow［J］.Journal of Fluid Mechanics，2006，562：35.

［9］ 马坤.多孔介质中湍流流动的数值模拟［D］.大连：大连理工大学，2009.MA Kun.Numerical simulation of turbulence flows in a porous media［D］.Dalian：Dalian University of Technology，2009.

［10］ 谢立全，刘曙光.土体渗流-切向水流相互作用机理分析［J］.同济大学学报：自然科学版，2010，38（7）：982.XIE Liquan，LIU Shuguang.Mechanism analysis of interactions between seepage and tangential flow［J］.Journal of Tongji University：Natural Science，2010，38（7）：982.

［11］ Ruff J F，Gelhar L W.Turbulent shear flow in porous boundary［J］.Journal of Engineering Mechanics，ASCE，1972，98：975.

［12］ Suga K，Matsumura Y，Ashitaka Y，et al.Effects of wall permeability on turbulence［J］.International Journal of Heat and Fluid Flow，2010，31：974.

［13］ Suga K，Mori M，Kaneda M.Vortex structure of turbulence over permeable walls［J］.International Journal of Heat and Fluid Flow，2011，32：586.

［14］ Pokrajac D，Manes C.Velocity measurements of a free-surface turbulent flow penetrating aporous medium composed of uniform-size spheres［J］.Transport in Porous Media，2009，78：367.