基于结构化模型的金融衍生品流动性分析

李少华，程远杰

（同济大学 数学系，上海200092）

对于流动性风险有很多刻画方法，目前国际金融界主要的研究结果有以下几种，认为流动性的大小可以由供求关系来确定，例如 Grossman and Miller［1］指出市场的流动性是由当前的供给关系决定的.Cetin等［2］在套利定价理论中加入了流动性风险，假设给定一条随机供给曲线的情况下，指出金融资产的价格是关于交易数量的函数，而流动性补偿则由资产价格和交易量同时决定.Jarrow等［3］假设交易价格是关于交易数量的函数，用随机供给曲线来描述流动性风险，给出了标的资产不具有完全流动性的情况下的期权定价.另一种认为流动性的大小可以由企业债券的收益利差来决定.收益利差是指在同等条件下不同流动性的企业债券的收益率之差；Amihud等［4］通过分析具有相同到期日的美国国库券，来分析流动性利差，同时它们的差值是一个关于到期时间的递减函数.为了能把流动性利差从企业债券的收益利差中分离出来，Longstaff等［5］先对流动性风险进行建模，此模型主要通过约化方法（reduced form models）来做的，其含义是将流动性假设成强度过程，这个强度一般用lt来表示，lt满足下面的随机微分方程dlt=K（θ-lt）dt+βdWt，其中K，θ，β为常数，Wt表示标准布朗运动.其次是通过流动性风险给投资者带来的损失来定量流动性风险，Zheng［6］描述了用结构化模型——structural models，来研究流动性风险和信用风险在金融衍生产品的定价中的相互影响，它的模型主要是通过假设企业总资产价值以及总资产的破产边界来描述流动性风险，Ericsson等［7］给出了一个同时具有流动性风险和信用风险的企业债券价格的结构化模型，并指出在企业债券利差中，流动性利差与信用利差具有正相关的关系，并且二者都是关于到期时间的递减函数.在定价领域中，关于流动性风险的内容还有其他很多方面的研究：Amihud等［4］介绍了流动性对证券定价的影响；Cetin等［2］研究了纳入流动性影响的期权定价；还有其他学者分析了流动性风险和信用风险对利率模型的影响.

流动性风险是指金融资产在转换成货币或货币等价物时，其价值不会蒙受损失的能力的大小，其实是一种综合性风险，它可以由操作风险，信用风险等风险引起，在本文中将流动性风险分离成两个部分：系统性流动性和个体流动性，前者是指市场中固有的流动性，对于不同的产品，该流动性是不会变化的，它是受市场整个环境以及财政政策等系统因素的影响，后者是指产品本身的流动性，也就是说不同的产品都有不同的变现能力，即随产品不同而变现能力不同的就是个体流动性差异所致.在理论研究金融衍生产品的定价时，通常考虑的是违约风险，忽略了流动性风险，而流动性风险可能会给投资者带来损失，这使得实际模拟验证时有些出入.在实际金融背景下，金融资产的信用风险和流动性风险是相互影响的，很难具体区分开来，不少金融专家都对此作了阐述，Zheng［6］假定信用风险发生时刻与流动性风险发生时刻是相互独立的，然后在此基础上进行了相关的研究，但在金融实践中，流动性风险和信用风险相互影响，在某种情况下，这种相互作用会使金融市场迅速恶化，因此对两个风险的非独立性研究显得尤为重要，为此，笔者在文章中给出了信用风险和流动性风险发生时刻不独立的损失值模型，最后提出流动性风险可以划分为两部分即市场的系统流动性以及特殊金融产品本身的流动性，并通过研究国债以及信用等级为AAA的企业债券的流动利差，来验证确实存在市场系统流动性和产品本身流动性.

1 流动性风险和信用风险的损失值模型

假设市场上有一组交易对手，A表示持有方，B表示发行方，对于持有方来说，不仅面临对手的违约风险，另外，一旦自己破产，亦存在清算时资产的变现问题，即流动性风险.已知 Ω，G，（P）是一个风险中性的概率测度空间，Ft是表示到时间t时市场变量（如股票价格，利率等）的信息，F=（Ft）t≥0是定义在Ω，G，（P）上的域流，其中∪t≥0Ft⊂G.

1.1 违约与清算时间相互独立的损失模型

首先假定τ1，τ2是定义在（Ω，G，P）上的非负随机变量，τ1为合约发行方违约的时刻，τ2为由于合约持有方破产而实施清算的时刻，τ=min（τ1，τ2）表示合约发行方违约和持有方清算合约二者先发生的时刻，V表示合约的价值.对于合约持有方来说，到期日为T的一份合约损失现金流如下：如果τ＞T，即合约到期前没有发生B违约和A清算的情况，A损失为零.如果t＜τ≤T，表示在合约生存期信用事件或流动性事件发生的情况：

（2）当τ=τ2时，持有方清算合约，则会遇到流动性风险，假设δ2为单位交易成本，δ3为一个固定的交易成本，若Vτ＜0，则持有方支付（1+δ2）·（-Vτ），损失为δ2（-Vτ），若Vτ＞0，则持有方的损失为δ2Vτ，损失为（1-δ2）Vτ，在该时刻的损失为δ2|Vτ|+δ3.

为了计算合约的损失值，先介绍下面几个基本性质：

性质1［6］若随机变量τ1，τ2满足下面的条件，对任意的T＞0和任意的t1，t2∈［0，T］，

式（1）表示在给定FT的情况下，τ1，τ2是相互独立的（主要为了提供一个简单的计算），式（2）表示两件事情不可能同时发生；

性质3 令｛Zt｝t≥0是一个有界F 可料过程，则对任意t＜T＜∞，

1.2 违约与清算时间非独立的损失模型

首先构造一个马氏链，知道该合约有4个状态：发行方不违约以及持有方没有发生清算，发行方违约以及持有方没有发生清算，发行方不违约以及持有方发生清算，发行发违约以及持有方发生清算同时发生.分别用1；2；3；4标注上述状态，即：Ct=1表示发行方不违约以及持有方没有发生清算；Ct=2表示发行方违约以及持有方没有发生清算；Ct=3表示发行方不违约以及持有方发生清算；Ct=4表示发行方违约以及持有方发生清算同时发生.相应的转移密度矩阵为Λ（t）=｛λij（t）｝i，j=1，2，3，4其中λij（t）∈Ft.假设转移密度矩阵服从Markov copula条件，即λ22=λ13+λ14，λ33=λ12+λ14.设λ12=λ1，λ13=λ2，，λ14=λ3，则转移密度矩阵Λ（t）可写为：

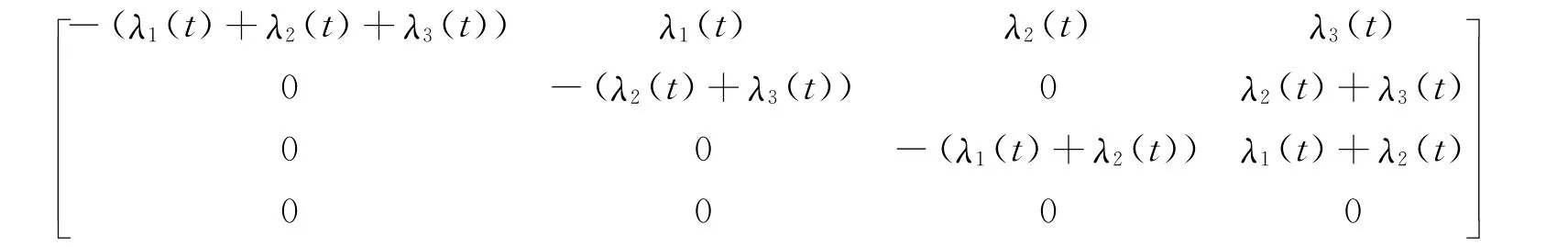
性质4 在转移密度矩阵下就可以有如下这些公式：

从而在前一部分的基础上，只要在总的损失中加入同时发生时刻损失现金流的贴现，就可得到一份合约的总损失Lt0为

1.3 利差模型

现对一份标准合约进行定价，如果Sti，i=0，1，2依次表示总利差，信用利差，流动性利差，rt表示无风险利率，则合约的现价为：VTe-（St0+r）（T-t），另一方面，由前面对损失值模型的分析其定价公式为：Vt-Lt0，对于同一份合约，其价值应该是一致的，于是有：

同理，对于信用利差和流动性利差分别用信用事件和流动性事件发生时带来的损失值进行定义，这样就得到所有利差的公式：

2 违约以及清算时间的分布

假设合约持有方清算时刻τ2服从参数为λ指数分布，Fui是τi＜u的条件分布，即合约持有方发生清算的概率为［7］

其中：r为无风险利率，σ为波动率；并且r、σ都是常数；Wt是标准的布朗运动.式（5）的解为

其中，A0是资产在初始时刻的值，m=r-σ2/2.

该模型的主要思想是结构化方法，当B公司的资产At低于某个常数边界L时，B公司发生违约，即τ1是资产Au第一次碰到L的时刻，τ1=inf｛u：Au＜L｝.知道公司B的生存概率即违约发生的分布函数，

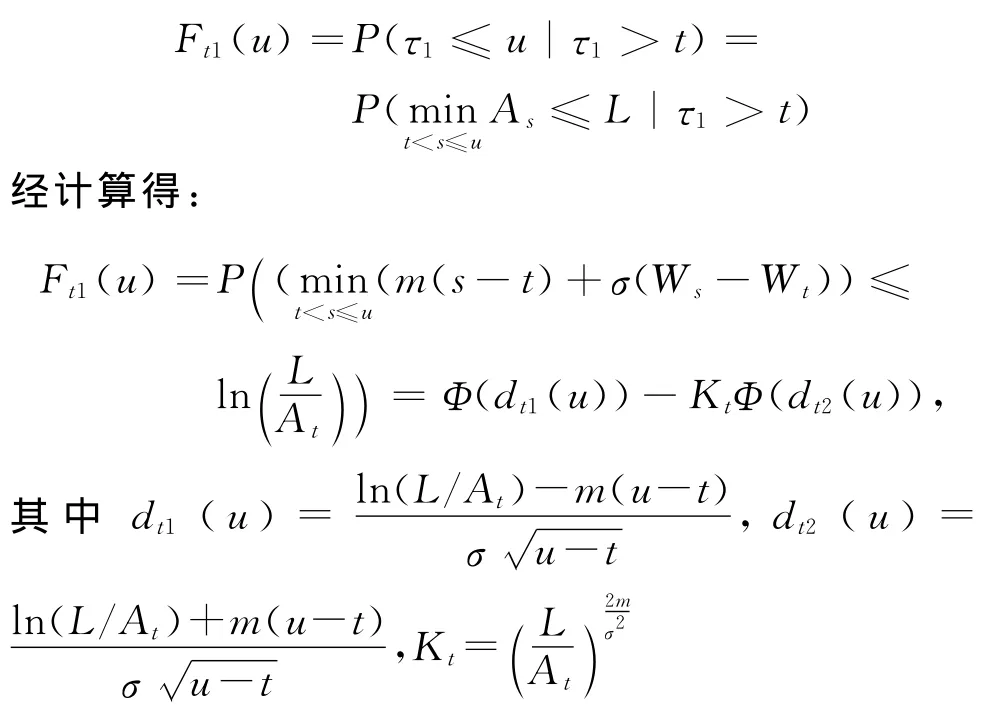
3 实证分析

利用债券市场的交易数据，通过第1.3节和第2节中的模型对利差的计算，来验证一份债券确实存在市场系统流动性和产品本身流动性.实证中需要假设认为国债的流动性利差为市场的流动性利差，企业债券的流动性利差包括市场的流动性利差以及债券本身的流动性利差，这样通过国债与企业债就可以把债券的流动性利差区分开来，表1是收集到的关于国债和企业债券的数据.

对于其他条件都相同但流动性不一样的两个资产，其二者收益率之差即为流动性利差.具体操作方法是通过债券交易市场获得的数据计算出债券的到期收益率，其次选取一年期银行间国债收益率作为无风险利率或者说基准利率，将二者作差得到的结果即为流动性利差，而本文选择一年期银行间国债主要从两方面来进行考虑，一是银行间的国债可以认为是无违约风险的（违约利差比较小，相对于流动性利差可以忽略不计），二是期限短，可以认为它的流动性比较好，甚至流动性的补偿为零，这样其他所有债券到期收益率与其之差就是该债券的流动性利差.由式（3）—（4）可知在没有考虑信用风险即Lt1=0的情况下，可知此时损失值公式表达式：

表1 国债和企业债的年化收益数据Tab.1 Treasury bonds and corporate debt in the yield data

那么通过前面每个观察点的数据，可以回归出流动性利差中的参数（表2），回归得到的模型统计量R2均高于0.8，

表2 利差回归参数Tab.2 The regression parameters of spread

有了表2的参数估计后，可以将国债和企业债券的流动性利差与剩余时间的关系用图1来表示，同时可以研究流动性利差的结构关系.

通过图1发现两个流动性利差之差大约在0.6至0.7个百分点左右，在不考虑信用利差的情况下，基于前面的实证假设，把国债的流动性利差认为是市场的流动性利差，国债与企业债的流动性利差之差作为债券本身的流动性利差来考虑.发现，在总的流动性利差中，整个债券市场的流动性利差占总流动性利差的比重较大，也就是说，市场上的每一份债券，它们的流动性不足主要是因为整个债券市场环境的流动性缺乏所致，但是，不同的企业他们发行的债券所面临的流动性不足大小各异，主要是因为债券本身的流动性不同所引起.

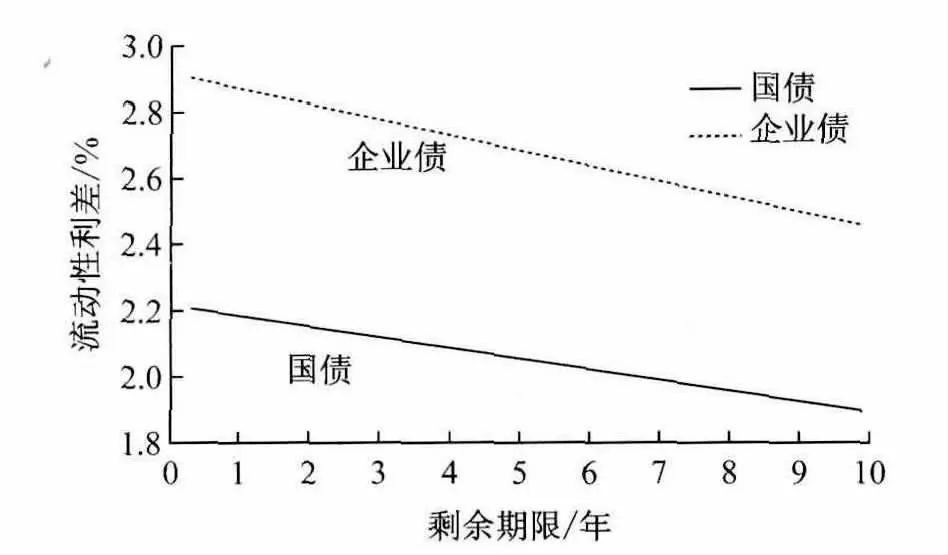
图1 国债与企业债流动性利差期限结构Fig.1 Treasury bonds and corporate debt maturity structure of liquidity spreads

4 主要结果

（1）本文主要研究了资产的流动性风险，在结构化模型的基础上，给出了信用风险以及流动性风险的损失值模型以及利差模型.

（2）流动性风险与信用风险是很难区分开来的，这个可以通过损失值模型容易发现，它们的表达式始终都包含了二者风险发生时刻服从的分布函数，从而在刻画两个风险时，很难将它们进行区分开来，它们的相关性是不容忽视的.

（3）在最后的实证部分主要基于无违约风险的债券进行流动性利差研究，可以发现两个结果：①是债券的流动性利差随着剩余时间的减小而增大的，并且接近呈线性函数关系；②是发现流动性利差可以看成有两部分来组成，即合约本身的流动性利差与市场环境的流动性利差，并且后者在总的流动性利差中占大部分（在75%左右），前者比重较小.

［1］ Grossman S J，Miller M H.Liquidity and market structure［J］.The Journal of Finance，1988，43（3）：617.

［2］ Cetin U，Jarrow R A，Protter P.Liquidity risk and arbitrage pricing theory［J］.Finance and Stochastics，2004，8（3）：311.

［3］ Jarrow R，Peotter P， Warachka M.Pricing options in a extended Black Scholes economy with illiquidity［J］.The Review of Financial Studies，2006，19（2）：493.

［4］ Amihud Y，Mendlson H.Liquidity，maturity，and the yields on U.S.treasury securities［J］.The Journal of Finance，1991，46（4）：1411.

［5］ Longstaff F A，Mithal S，Neis E.Corporate yield spread：default risk or liquidity？new evidence from the credit-default swap market［J］.The Journal of Finance，2005，60（5）：2213.

［6］ Zheng H.Interaction of credit and liquidity risks：Modelling and valuation［J］.The Journal of Banking ＆Finance，2006，30：391.

［7］ Ericsson J，Renault O.Liquidity and credit risk［J］.The Journal of Finance，2006，16（5）：2219.